4.2. Пропускная способность каналов связи и теоремы оптимального кодирования.

4.2.1. Пропускная способность дискретного канала без помех.

Скорость передачи информации – среднее количество информации, передаваемое по каналу информации за единицу времени.

Если передаваемая 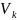символов в единицу времени, а среднее количество информации на 1 символ 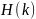, то скорость передачи информации по каналу будет равна:

Формула 1:

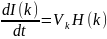
С другой стороны, средняя скорость поступления информации от источника сообщения называется его производительностью. И, если источник выдает 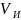символов в единицу времени, то его производительность мы можем охарактеризовать следующим образом:

Формула 2:

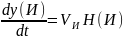
Скорость передачи информации по каналу без помех, определяемая Формулой 2, зависит как от технических характеристик канала (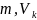 ), так и от статистических свойств входного сообщения (его избыточности в частности). Поэтому, для сравнения возможностей различных каналов, надо зафиксировать избыточность входного сообщения. Удобнее всего взять безызбыточное сообщение, которое обладает максимальной энтропией.

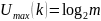
Тогда максимально возможная скорость такого канала оказывается равной:

Формула 3:

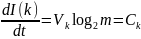– пропускная способность канала

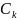- характеризующая максимальную скорость передачи по каналу, характеризующаяся данными техническими характеристиками.

Из Формулы 1 и Формулы 3 видно, что в общем случае при избыточности входного сообщения отличным от 0, скорость передачи по каналу меньше его пропускной способности.

Шеннон доказал, что принципиально возможно обеспечить скорость передачи по каналу без помех сколь угодно близкую к его пропускной способности.

Из этого следует, что условием согласования источника с каналом служит соответствие производительности источника и пропускной способности канала.

Вернемся к понятию типичных и нетипичных последовательностей символов и рассмотрим их свойства.

Рассмотрим простейший случай:

- длина алфавита, его мощность

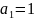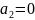, - символы алфавита

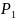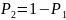, - вероятности появления символов

Рассмотрим свойства длинных последовательностей таких символов. Вероятность того, что в последовательности символов будет раз повторятся и раз - определяется биноминальным законом:

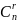– количество различных последовательностей содержащих символов и символов .

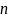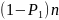При увеличении общего количества символов значение и в каждой реализации будут стремиться к и соответственно.

Именно такие последовательности и называются типичными. Вероятность появления других последовательностей будет малой. Закон больших чисел гласит:

При 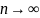вероятность появления типичной последовательности (с соотношением символов соответствующим им вероятностям) стремится к 1, а вероятность появления других стремиться к 0.

В этих типичных последовательностях будет встречаться раз, а - раз.

Аналогичный результат получается для алфавита из 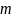символов. В этом случае типичной последовательностью длительностью будет являться:

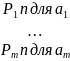
Число различных последовательностей будет равно:

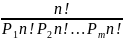
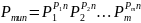
Этот результат может быть обобщен и на случай корреляции между символами, когда можно выделить типичные последовательности с кратностью определенных символов и их сочетаний, соответствующей статистическим свойствам источника сообщений.

Мы можем выявлять вероятность не только отдельных символов, но и их сочетаний. При этом все типичные последовательности будут равновероятными и их суммарная вероятность стремится повысится при .

Рассмотренные свойства последовательности символов большой длительности могут быть обобщены следующей теоремой асимптотической равновероятности.

Теорема. Любая реализация последовательности длительностью , выдаваемая стационарным источником (случайного процесса), при достаточно большой с вероятностью, стремящейся к 1, совпадает с одной из равновероятных типичных последовательностей.

Число 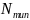(источника) может быть выражено через энтропию источника . Посколку при источник с вероятностью близкой к 1 выдает типичные последовательности, имеющие равную вероятность 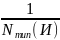, то информация содержащаяся в такой последовательности равна 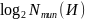. С другой стороны в символах будет содержаться информация равная . Приравниваем эти два результата:

Формула 1.

Типичная последовательность - такая, где реализовались статистические свойства источника, источник «выговорился».

Как было показано, для источника с объемом алфавита и избыточностью :

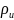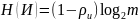
Следовательно, из Формулы 1 получаем:

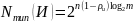
Определим число всевозможных последовательностей при объеме алфавита :

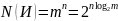
Найдем долю, которой соответствуют типичные последовательности от общего их числа:

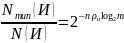
Отсюда следует, что при избыточности источника и при , предел этого соотношения будет равен 0, т.е. если источник обладает избыточностью, то с увеличением длительности последовательности символов все меньшая доля от всевозможных последовательностей, называющиеся типичными участвуют в передаче информации. Лишь безызбыточные источники создают последовательности сплошь типичные, и все они в равной мере участвуют в передаче информации.