8.5. Конечно-элементные методы

Первые применения метода конечных элементов относятся к середине ХХ века [Каплун]. Широкое применение метод получил в разнообразных задачах математической физики (механика деформируемого тела, механика несжимаемой жидкости, теплоперенос в механике сплошных сред и др.), строительной механики, теории электрических цепей и других. Ниже излагаются лишь отдельные элементы метода применительно к задачам о напряженно-деформированном состоянии инженерных конструкций. Систематическое изложение метода конечных элементов имеется, например, в [Норри].

Отметим следующие особенности метода конечных элементов, отличающие его от конечно-разностных и интегро-интерполяционных методов.

1. Задание геометрии конечных элементов

Построение вычислительных алгоритмов осуществляется для конечных элементов, форма которых может быть линейной, плоской или пространственной формы.

При решении задач о напряженно-деформированном состоянии твердых тел как линейные могут приниматься упругий элемент типа упругой пружины, стержень, балка. При решении задач электротехники – элементы типа резистор, емкость, индуктивность и т.п.

Плоские конечные элементы, как правило, имеют вид треугольников или (и) четырехугольников (рисунок 8.22). Треугольные и четырехугольные элементы могут иметь различную степень свободы (линейные, квадратичные, кубические и другие элементы).

Пространственные конечные элементы выбираются в виде тетраэдров, пятигранников или шестигранников (рисунок 8.23). Допускается применение в решаемой задачи конечных элементов различной формы и различной размерности.

В зависимости от решаемой задачи помимо задания геометрии конечного элемента и его ориентации в пространстве необходимо задать его физические свойства и связи.

2. Функциональные зависимости внутри конечного элемента

Искомая функция, являющаяся решением поставленной задачи, внутри каждого конечного элемента представляется полиномом той или иной степени, в зависимости от выбранного типа конечного элемента.

Для конечных элементов линейного типа могут использоваться модели линейной интерполяции. Так, для функции f, изменяющейся на интервале от до зависимость f(x) можно представить в виде

. (8.166)

Здесь , (функции называют коэффициентами формы). Важным свойством коэффициентов формы является равенство - . Кроме того, можно отметить, что уравнение (8.166) очень близко по написанию к уравнению (2.27) главы 2, полученному при использовании для интерполирования полиномов Лагранжа. Полиномы Лагранжа различных степеней часто используются при интерполировании в конечно-элементных методах. При этом коэффициенты формы в узловых точках (точки, в которых известны значения функции) принимают значения 0 или 1. Наряду с полиномами Лагранжа часто используются Эрмитовы полиномы.

Рассмотрим, как выполняется интерполирование значений функции внутри конечного элемента при использовании линейных треугольных конечных элементов (рисунок 8.24). На рисунке 8.24а элемент размещается в глобальной координатной системе xy, на рисунке 8.24б приводится локальная система координат , связанная с вершинами треугольного элемента 1, 2, 3. Соотношения, позволяющие связать координаты вершин треугольника в глобальной и локальной системе координат, относительно несложны, и не приводятся. В то же время запись интерполяционной зависимости для произвольной изменяющейся в треугольном элементе функции f в локальной системе координат представляется очень простой. В соответствии с рисунком 8.24 можно записать следующую интерполяционную зависимость для функции

. (8.167)

Здесь , , - коэффициенты формы.

Представленных примеров достаточно, чтобы написать общую интерполяционную зависимость для других вариантов конечных элементов:

- квадратичный треугольный элемент (рисунок 8.25)

. (8.168)

Здесь , , , , , . Условие выполняется;

- линейный четырехугольный элемент (рисунок 8.26)

. (8.169)

Здесь , , , Условие выполняется;

- квадратичный четырехугольный элемент (рисунок 8.27)

. (8.170)

Здесь , , , , , , , . Условие выполняется.

Варианты интерполирования значений функции f при использовании других типов конечных элементов рассматриваются в [Норри].

3. Дискретизация исходной задачи

Дискретизация задачи в методе конечных элементов с использованием интерполяционных полиномов может быть выполнена для дифференциального уравнения или для эквивалентного варианта, сформулированного в вариационной постановке. Так, например, стационарное уравнение теплопроводности , заданное на плоскости xy с граничными условиями Дирихле (на границах задаются значения температуры) и Неймана (на границах задаются значения тепловых потоков) эквивалентна задаче о минимизации функционала . Здесь - функции из множества допустимых пробных функций, заданных в плоскости xy. Пробные функции должны быть непрерывны, иметь кусочно-непрерывные первые производные и удовлетворять граничным условиям исходной задачи [Норри].

Оба подхода одинаково часто используются в различных версиях метода конечного элемента, однако можно утверждать, что более предпочтительной в последнее время является дискретизация исходных дифференциальных уравнений.

4. Применяемые вычислительные методы

Дискретизация дифференциальных уравнений или вариационной задачи для совокупности конечных элементов сводит исходную задачу к решению системы линейных алгебраических уравнений вида . Как правило, матрица коэффициентов в этой системе уравнений имеет диагональный вид либо сильно разрежена. Методы решения таких систем уравнений рассмотрены в разделе 8.3.3.

Рассмотрим простейшие примеры решения некоторых задач о напряженно-деформированном состоянии твердых тел методом конечных элементов, заимствованные в [Каплун]. Другие применения метода конечных элементов в задачах о напряженно-деформированном состоянии можно найти в [Аликин,Дульнев,Каплун] и др.

Выше отмечалось, что простейшие конечные элементы – это линейные элементы, искомая функция для этих элементов является функцией одной пространственной переменной. В задачах о напряженно-деформированном состоянии твердого тела как линейные могут приниматься упругий элемент типа упругой пружины (рисунок 8.28), стержень (рисунок 8.29), балка (рисунок 8.30).

Элемент типа упругой пружины характеризуется жесткостью k, связывающей изменение линейного размера пружины с величиной приложенной к пружине силе P - .

Для элемента, представленного на рисунке 8.28, в узлах 1 и 2 приложены силы , что приводит к перемещению этих узловых точек, соответственно, на величины . Связь сил и перемещений в узлах 1 и 2 может быть записана в виде

,

.

В матричном виде система линейных алгебраических уравнений для рассмотренного простейшего линейного элемента запишется

.

На рисунке 8.31 представлена схема системы, состоящей из двух линейных упругих элементов. Жесткости этих элементов отличаются. По аналогии с выше записанным для первого и второго элементов можно записать следующие матричные уравнения

,

.

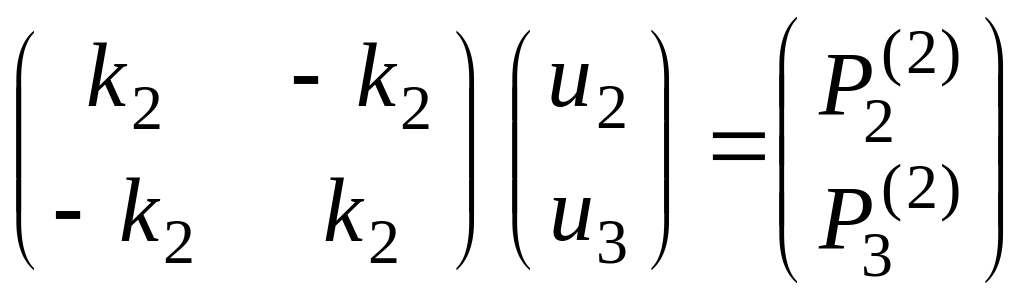В линейных задачах, в том числе, и в рассматриваемой задаче, возможно применение принципа суперпозиции, и это позволяет суммировать нижнее и верхнее матричные уравнения

После обозначения , , последнее матричное уравнение принимает окончательный вид

.

Рассмотрим следующий пример. Cтержень (рисунок 8.29) характеризуется длиной L, площадью поперечного сечения F и модулем упругости E. Модуль упругости связывает осевое перемещение и относительную деформацию с напряжениями , возникающими в стержне формулой

.

Из [СправочникПолянин] известно, что жесткость стержня может быть установлена зависимостью . Таким образом, рассматриваемая задача сводится к задаче о деформации упругого элемента, рассмотренной выше. Матричное уравнение, связывающее перемещения u и силовые нагрузки P в этой задаче имеет вид

.

Следующий пример конечного элемента - «балка», которая характеризуется длиной L, моментом инерции площади поперечного сечения I и модулем упругости E. Балка имеет две степени свободы, она характеризуется линейным прогибом и углом поворота . На левой и правой границах балки действуют перерезывающие силы и изгибающие моменты , действующие в плоскости . Изменение угла поворота для балки устанавливается соотношением - .

Матричное уравнение, связывающее перерезывающие силы и изгибающие моменты с прогибами и угловыми перемещениями , в рассматриваемой задаче записывается следующим образом [Каплун]

.

На практике рассматривается и комбинация элементов – «стержень+балка». Такая комбинация рассматривается как линейная (допускается принцип суперпозиции) и позволяет учитывать не только сдвиговые нагрузки и изгиб, но и силовые нагрузки вдоль элемента (осевые нагрузки).

Для плоских конечных элементов удается составить матричное уравнение, связывающее перемещения с относительной деформацией или (и) с напряжениями . С учетом коэффициентов формы перемещения в плоском конечном элементе можно представить в виде или .

Относительная деформация может быть установлена следующим образом

.

В матричном виде последнее уравнение запишется

Здесь - матрица дифференциальных перемещений

.

Напряжения запишутся в матричном виде

.

В [Каплун] приводится дальнейшее преобразование последнего матричного уравнения, которое приводится к виду

.

В последнем матричном уравнении - матрица жесткости элемента, - матрица силовых воздействий. Матрица жесткости устанавливается интегрированием по объему конечного элемента

.

В задачах о напряженно-деформированном состоянии для плоских конечных элементов принципиальной является его толщина. В зависимости от отношения толщины элемента к его характерному размеру в качестве расчетных соотношений используются уравнения из теории тонких или толстых пластин. С учетом уравнения для матрицы жесткости следует учитывать и возможное изменение толщины вдоль конечного элемента.

В [АлиевСуворов] рассматривается применения метода конечных элементов при решении задач теплопроводности в смесевых твердых топливах (металлизированных и безметальных).

Необходимость и целесообразность применения конечных элементов в задачах о прогреве твердого топлива иллюстрируется рисунком 8.32. В состав смесевого топлива входит горючее (например, каучук), которое одновременно является связующим всех компонентов, окислитель (например, перхлорат аммония), легковоспламеняющиеся металлы (например, алюминий). Размеры частиц окислителя могут составлять 10…100 мкм, частиц алюминия – 1…10 мкм. Толщина прогретого слоя твердого топлива в условиях камеры сгорания двигательной установки не превосходит 300…500 мкм. Такая структура смесевого твердого топлива делает непригодной модель твердого топлива как гомогенного материала, применяемую при расчете прогрева баллиститных топлив [Соркин, Ассовский]. Действительно, теплофизические характеристики основных материалов, входящих в состав смесевого топлива могут отличаться более чем в тысячу раз.

На рисунке 8.33 представлены расчетные схемы, использовавшиеся при анализе процесса прогрева твердого топлива. Из-за ограниченности вычислительных ресурсов анализ нестационарного процесса выполнялся в двухмерной постановке для элемента топлива, ограниченного размерами . Расчетная область формировалась набором конечных элементов треугольного типа. Количество конечных элементов принималось от 5000 до 50000. Для сравнения на рисунке 8.34 представлены результаты расчета прогрева смесевого металлизированного топлива (рисунок 8.34а) и безметального топлива (рисунок 8.34б).

Другая задача, связанная с прогретым состоянием твердого топлива – это задача о регулировании процессов зажигания и скорости горения топлива с использованием тепловых ножей или неизвлекаемых теплопроводных элементов, размещенных в теле заряда твердого топлива ([УправляемыеПетренко], рисунок 8.35). В этих задачах, как и в предыдущей, также существенна неоднородность теплофизических характеристик нагреваемых материалов. Внутри нагреваемого элемента конструкции теплофизические характеристики могут изменяться скачкообразно, при этом значения коэффициентов теплопроводности, удельных теплоемкостей могут изменяться на порядки. Кроме того, в прогретом слое топлива могут происходить фазовые переходы и химические реакции экзо- или эндотермического типа.

На рисунке 8.36 приводятся результаты расчета нагрева твердого топлива с вложенным в него перпендикулярно поверхности алюминиевым элементом. Расчетная область симметричная, поэтому расчет выполнялся в полуплоскости. На рисунке представлено температурное поле прогрева в зоне контакта теплопроводного элемента и пороха «Н». Значения координаты z, соответствующие расположению теплопроводного элемента - z ≤ 2,50 мм. При z > 2,50 мм размещается порох «Н». Результаты расчетов показывают, что прогрев материала в окрестности теплопроводного металлического элемента происходит со значительно меньшей скоростью, чем прогрев пороха. В итоге порох, размещенный в отдалении от теплопроводного элемента, воспламеняется раньше, чем порох, контактирующий с металлом.

Перечисленные выше закономерности представляются важными при проектировании новых элементов, входящих в состав зарядов твердого топлива.

Другие применения метода конечных элементов можно найти в многочисленной отечественной и зарубежной литературе. Кроме того, следует учесть, что основные алгоритмы метода конечных элементов реализованы в применяемых на практике программных коммерческих и некоммерческих продуктов (например, ANSYS, Solid Works, Pro Engeneer и др.).