2.2. Частные производные высших порядков
Пусть имеем функцию двух переменных
.
Частные производные
и
,
вообще говоря, являются функциями
переменных
и
.
Поэтому от них можно снова находить
частные производные. Следовательно,
частных производных второго порядка
от функции двух переменных четыре,
так как каждую из функций
и
можно дифференцировать как по
,
так и по
.
Вторые частные производные обозначают
так:
:
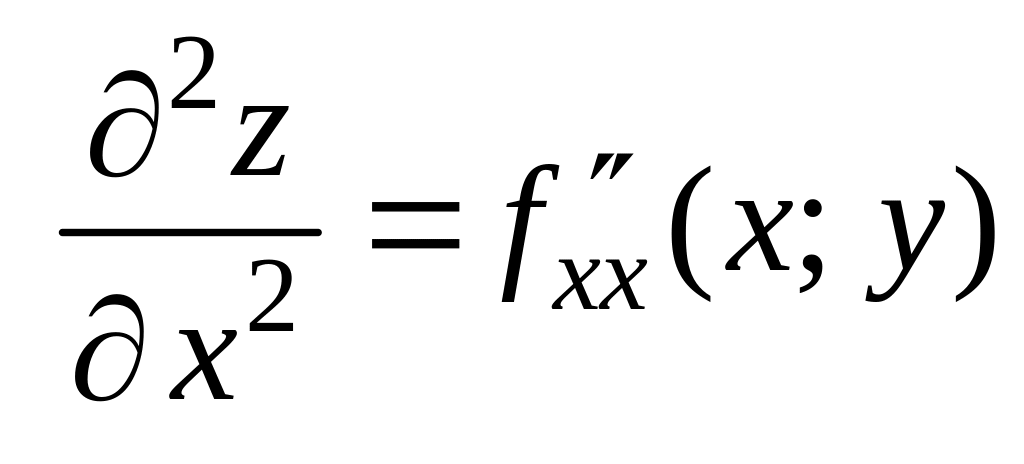здесь
дифференцируется последовательно два
раза по
;
:
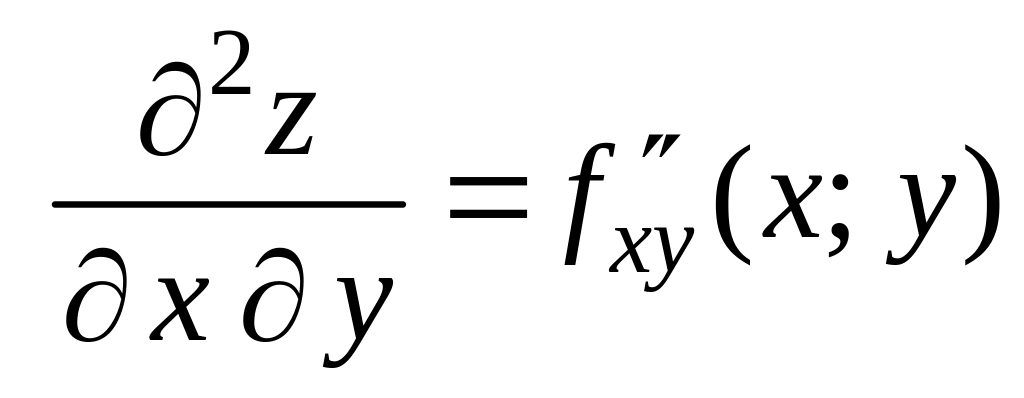здесь
дифференцируется последовательно по
,
а потом
результат дифференцируется по ;
:
здесь
дифференцируется последовательно по
,
а потом
результат дифференцируется по ;
:
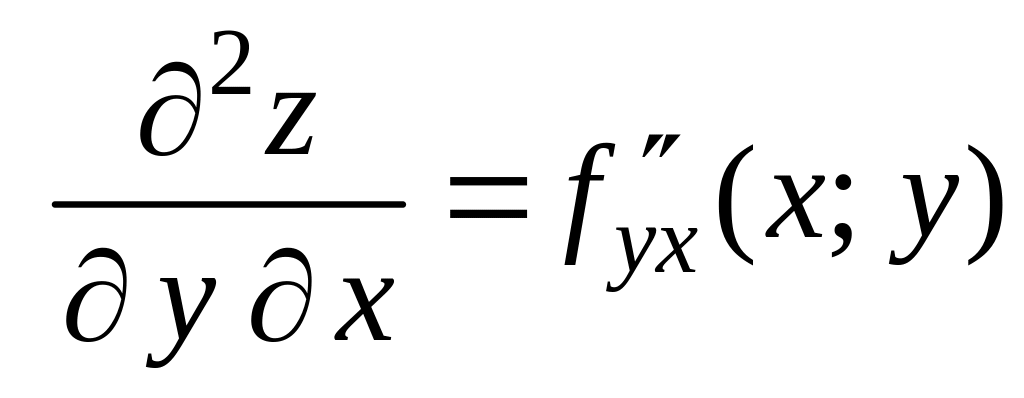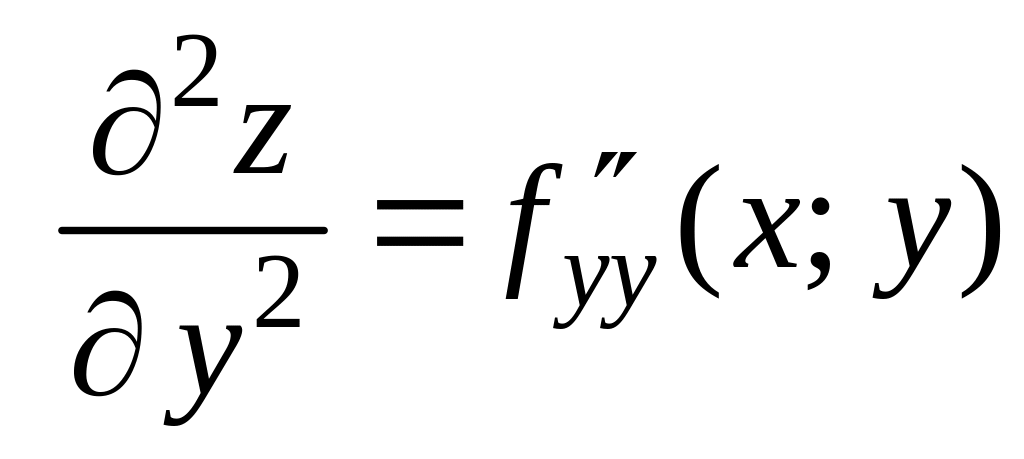здесь
дифференцируется последовательно два
раза по
;
Производные второго порядка можно снова
дифференцировать как по
,
так и по
.
Получим частные производные третьего
порядка. Например,
,
,
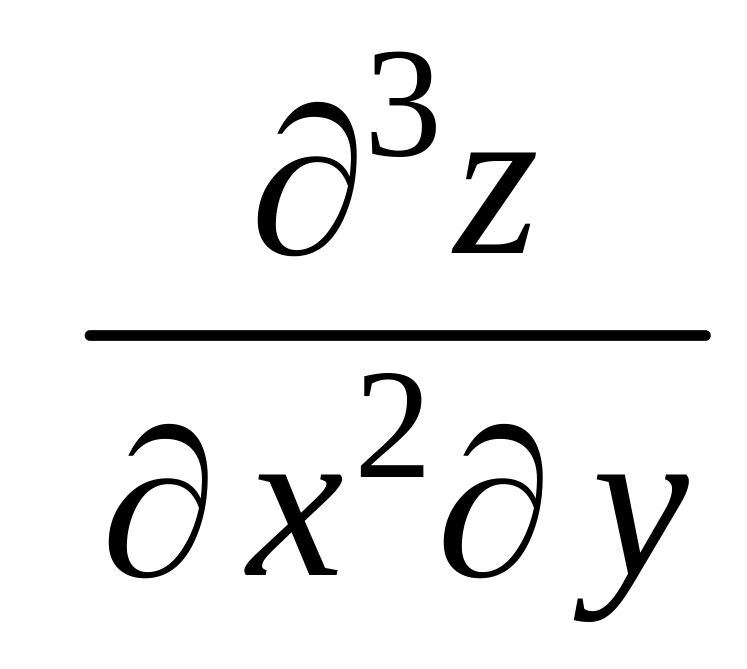и т.д. Аналогично определяются частные
производные четвертого и выше порядка.
Вообще, частная производная n-го
порядка есть первая производная
от производной (n1)-го
порядка. Например,
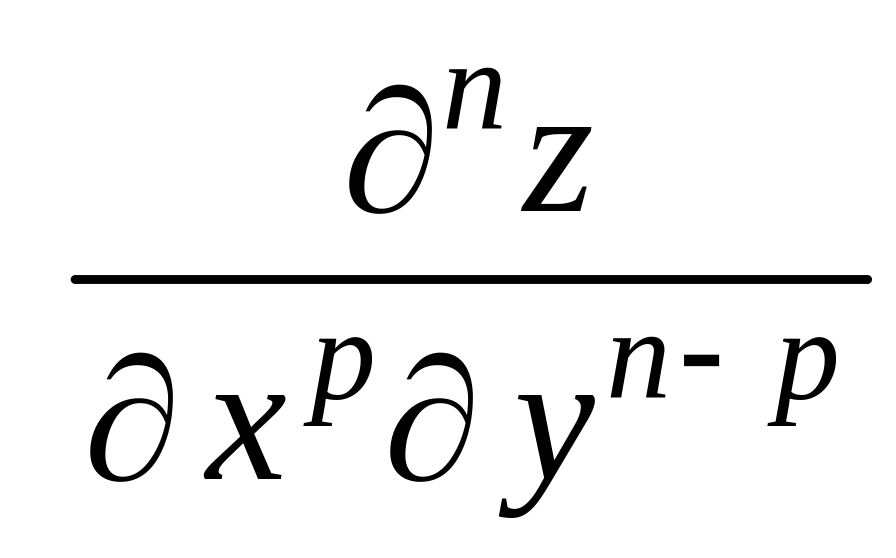есть производная n-го
порядка – здесь функция
сначала
раз дифференцируется по
,
а потом
раз по
.
Частная производная второго или более
высокого порядка, взятая по различным
переменным, называется смешанной
частной производной. Например,
,
.
Для функций любого числа переменных частные производные высших порядков определяются аналогично.
Пример 2.3. Найти частные производные второго порядка для функции:
.
Решение. Находим частные производные первого порядка:
.
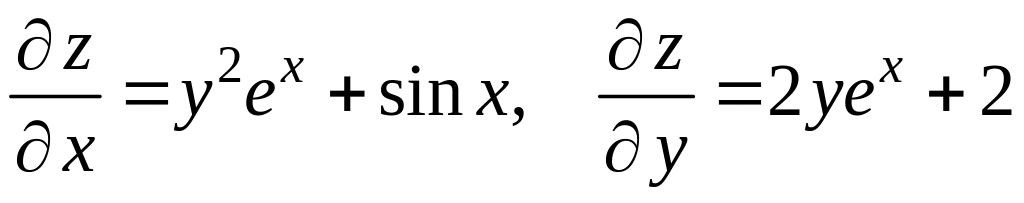Находим частные производные второго порядка:
,
,
,
.
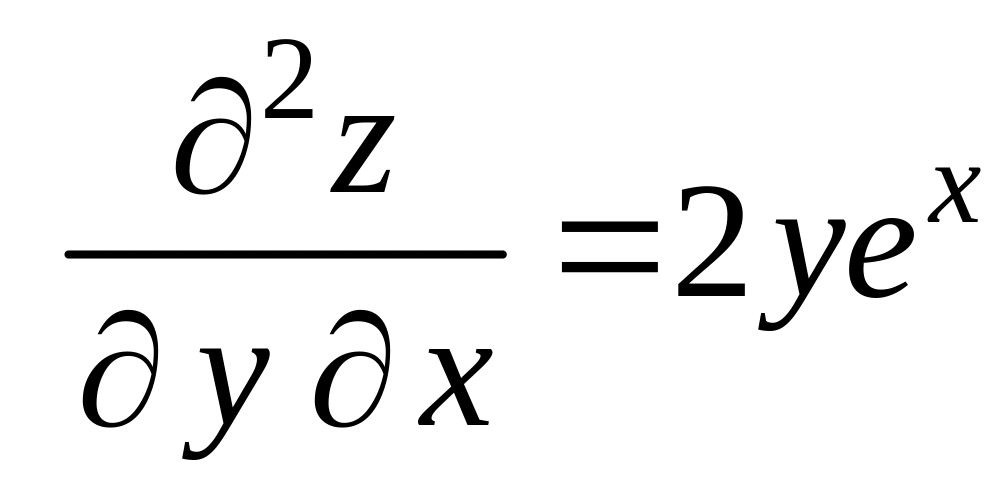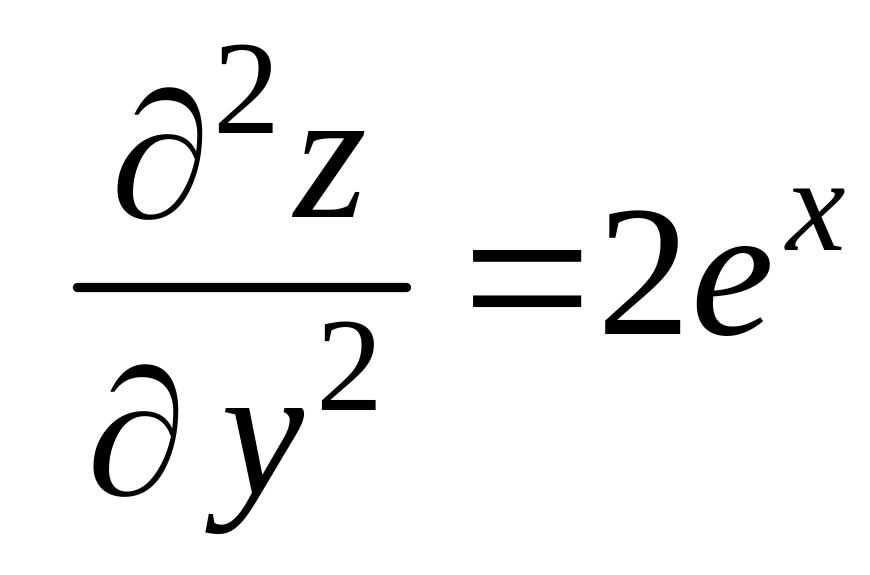Пример 2.4. Найти
,
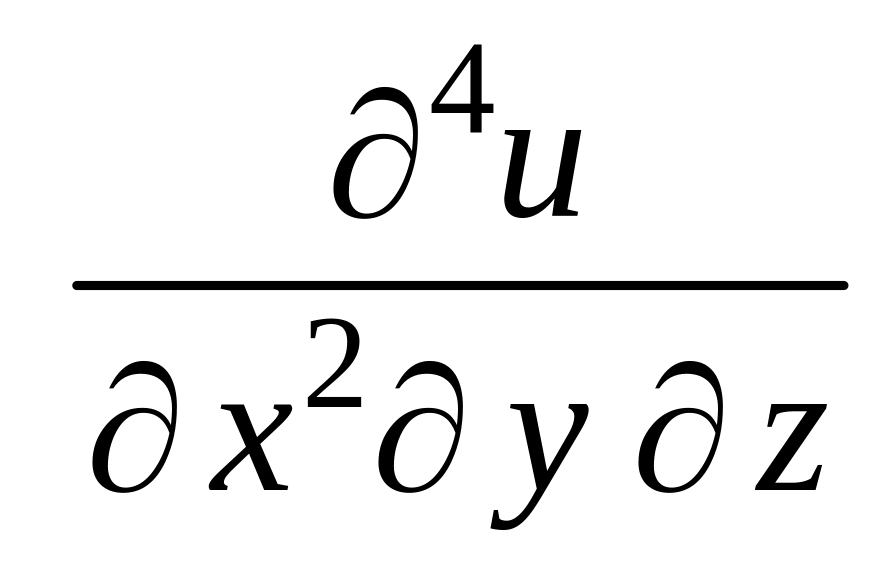если
.
Решение. Находим последовательно частные производные:
,
,
,
.
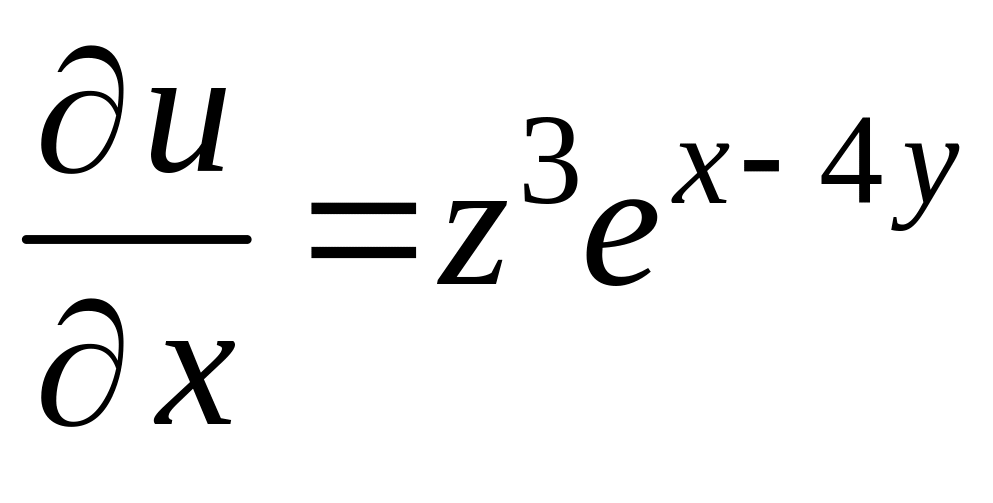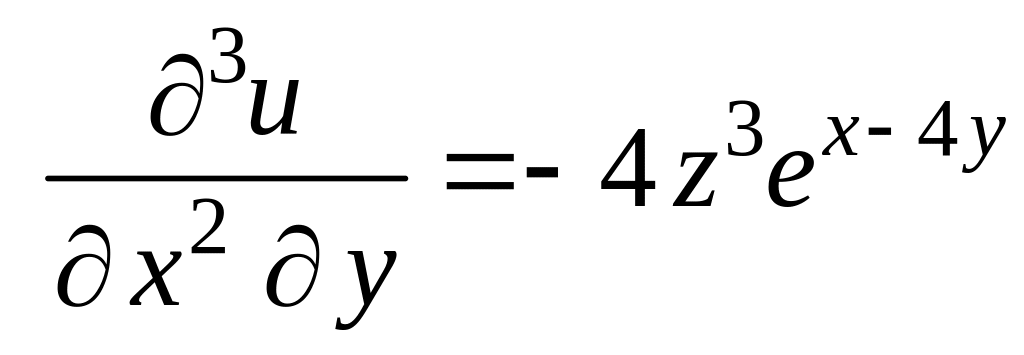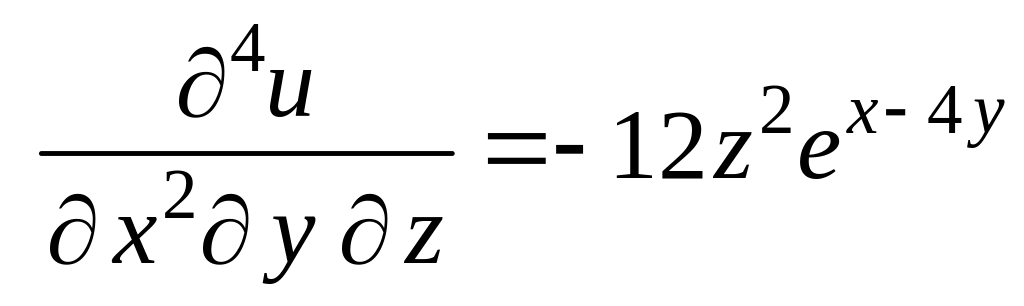Из примера 2.3. видно, что
.
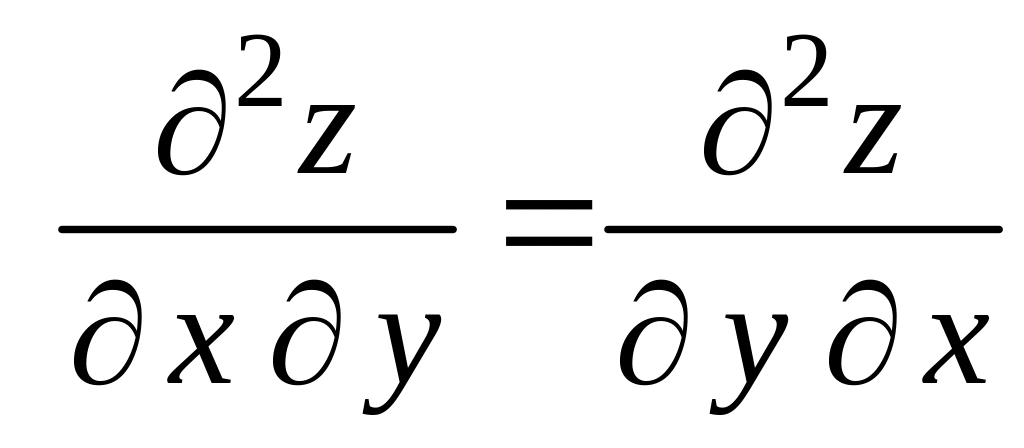И это не случайно. Имеет место теорема,
которую примем без доказательства.
Теорема 2.1 (теорема Шварца). Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.
В частности, для имеем .
2.3. Дифференцируемость и полный дифференциал функции
Пусть функция определена в некоторой окрестности точки . Составим полное приращение функции в точке :
.
Определение 2.3. Функция называется дифференцируемой в точке , если ее полное приращение в этой точке можно представить в виде
,
(2.3)
где
и
при
.
Сумма первых двух слагаемых в равенстве (2.3) представляет собой главную часть приращения функции.
Определение 2.4. Главная часть
приращения функции
,
линейная относительно
и
,
называется полным дифференциалом
этой функции и обозначается символом
:
.
(2.4)
Выражения
и
называются частными дифференциалами.
Для независимых переменных
и
полагают
и
.
Поэтому равенство (2.4) можно представить
в виде
.
(2.5)
Надо отметить, если функция
дифференцируема в точке
,
то она непрерывна в этой точке, имеет в
ней частные производные
и
,
причем
,
.
Тогда формула для вычисления полного
дифференциала примет вид:
.
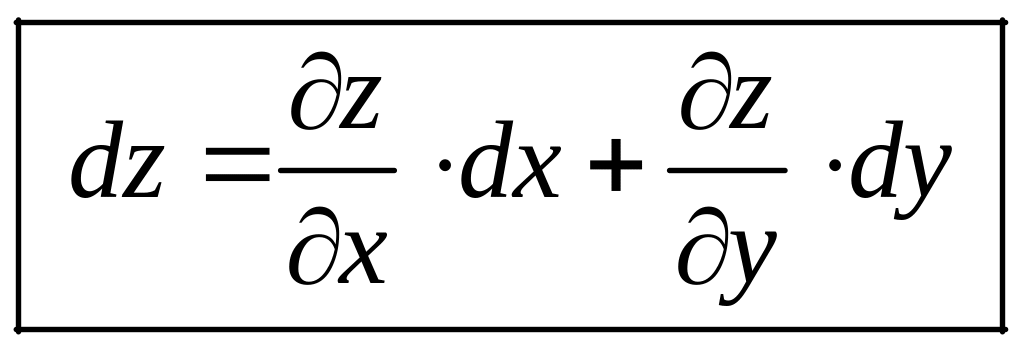(2.6)
Для функции
переменных
полный дифференциал определяется
выражением
.
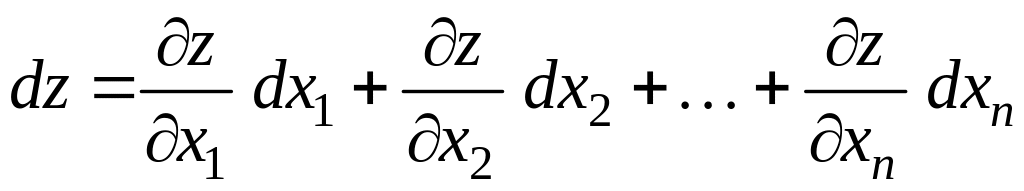(2.7)
Пример 2.5. Найти полный дифференциал
функции
.
Решение. Находим частные производные первого порядка:
,
,
.
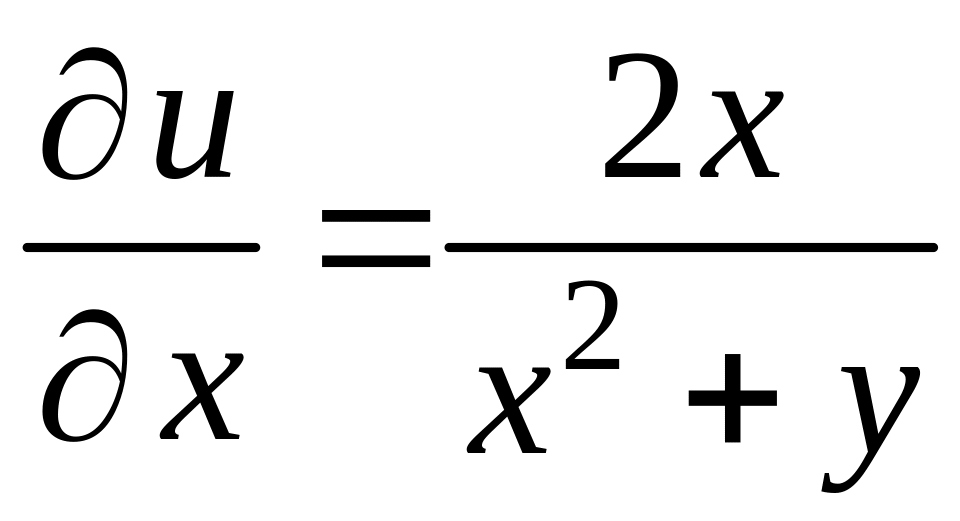Согласно формуле (2.7) получаем
.
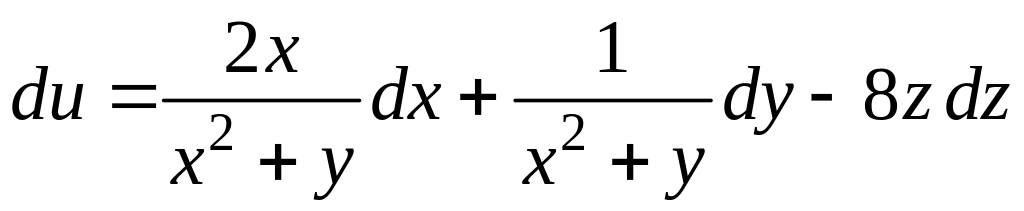Полный дифференциал функции (формула (2.6)) называется также дифференциалом первого порядка.
Введем понятие дифференциала высшего
порядка. Пусть функция
имеет непрерывные частные производные
второго порядка. Дифференциал второго
порядка определяется по формуле
.
Найдем его:
.
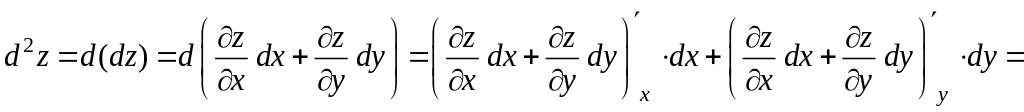
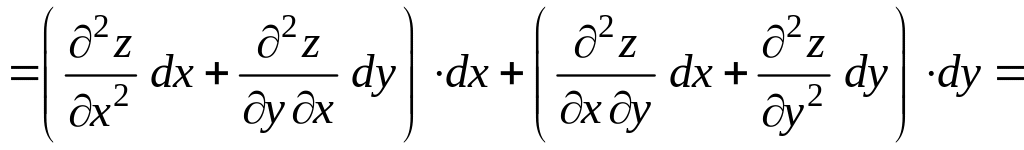
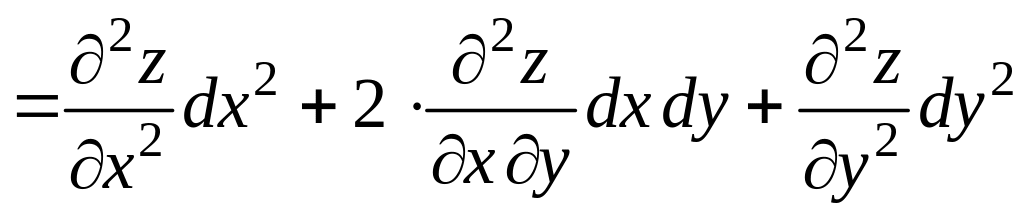Итак,
.
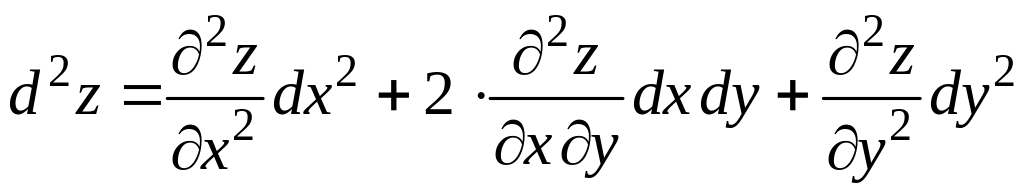(2.8)
Аналогично можно получить формулы для дифференциала третьего и более высокого порядков.
Пример 2.6. Найти
,
если
.
Решение. Находим частные производные первого порядка:
.
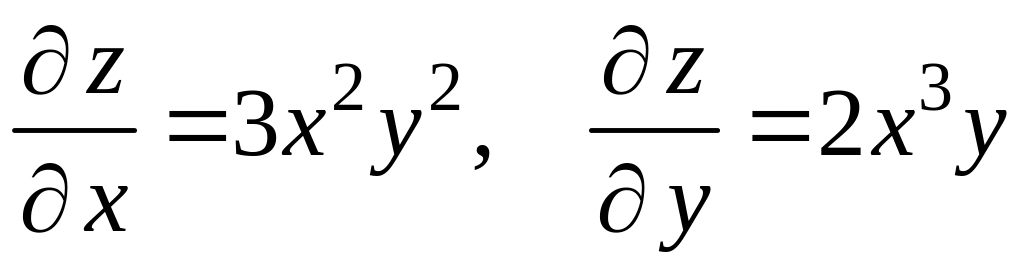Находим частные производные второго порядка:
,
,
.
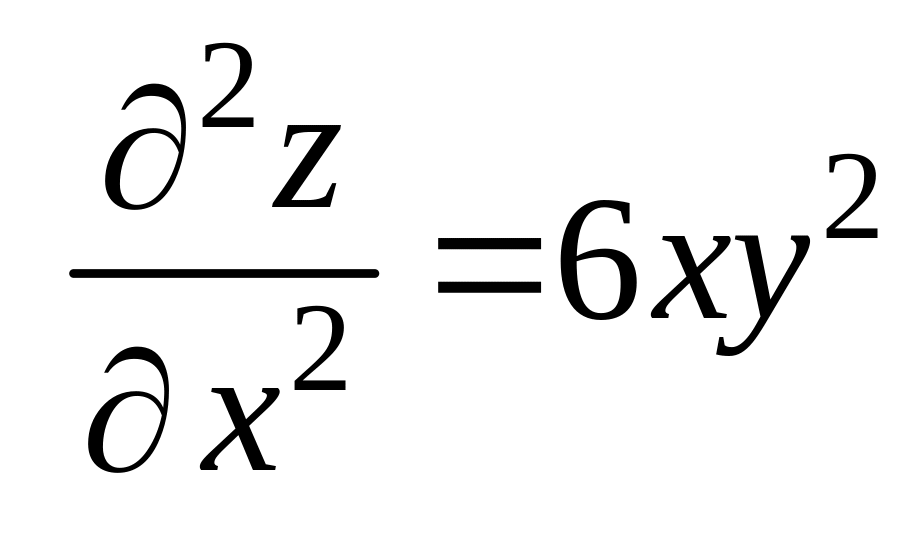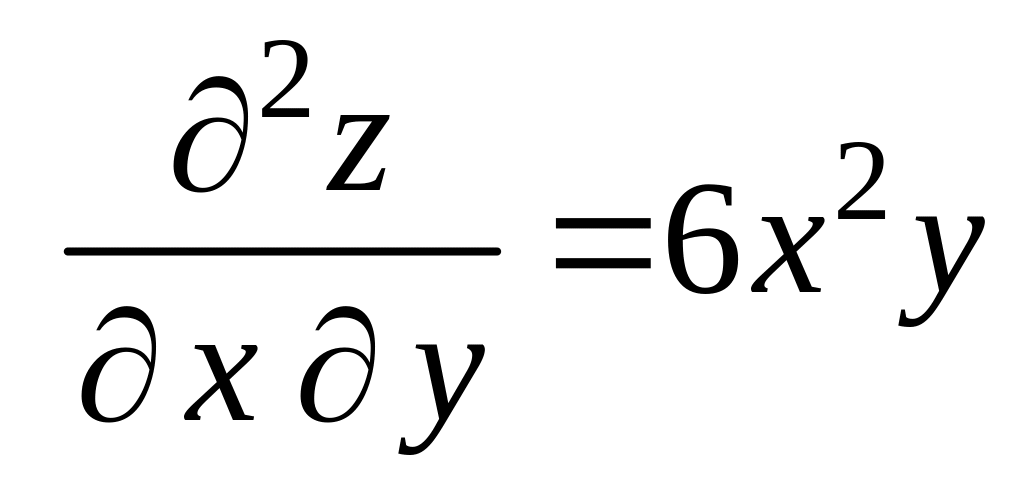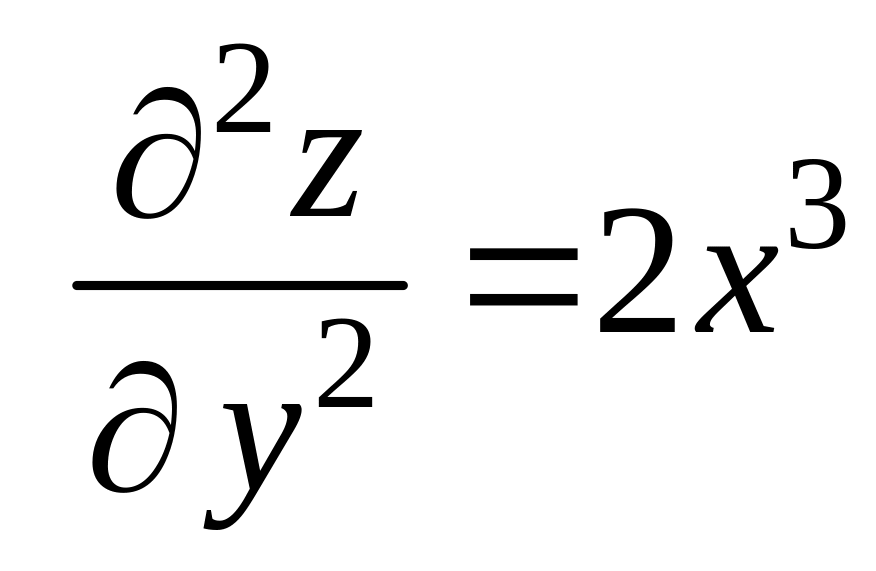Согласно формуле (2.8) получаем
.