4. Алгебраические и частотные критерии устойчивости замкнутых систем автоматического регулирования.

Исследование условий устойчивости САР может быть выполнено путем определения знака корней характеристического уравнения, соответствующего дифференциального уравнения, описывающего данную САР. Чтобы определить, затухают или не затухают возникшие колебания в САР, т.е. устойчива САР или неустойчива, достаточно определить знаки у всех вещественных корней и у всех вещественных частей сопряженно комплексных комплексных корней рассматриваемого характеристического уравнения. САР будет устойчивой, если все вещественные корни и вещественные части сопряженно комплексных корней будут отрицательными. В противном случае САР неустойчива. В случае сложных систем регулирования характеристические уравнения получаются высоких порядков и их решение затруднительно. Поэтому в целях облегчения решения практических задач, связанных с определением условий устойчивости САР, в разное время были выявлены признаки, позволяющие судить об устойчивости системы, не прибегая к решению характеристических уравнений. Эти признаки впоследствии получили название критериев устойчивости САР. Наиболее распространенные критерии устойчивости могут быть разделены на две основные группы:

а) алгебраические критерии, основанные на изучении знаков коэффициентов характеристического уравнения и знаков комбинации этих коэффициентов, например критерий Рауса-Гурвица;

б) частотные критерии, основанные на изучении расположения частотных характеристик в комплексной плоскости, например, частотный критерий А.В. Михайлова, применяемый для изучения сложных многоконтурных систем, рассматриваемых при этом в виде замкнутых систем регулирования, и критерий Найквиста-Михайлова, применяемый для простых одноконтурных систем, рассматриваемых в целях упрощения анализа в виде разомкнутых систем регулирования.

Особенностью всех частотных критериев, применение которых сопровождается графическими построениями на комплексной плоскости, является их наглядность. Особенностью же всех критериев устойчивости регулирования, в том числе и частотных, является то, что с их помощью можно решить только один вопрос, устойчива система регулирования или неустойчива. Ответа на вопрос о качестве регулирования, т. е. о величине отклонений регулируемой величины от нормального или заданного значения, о периоде и времени затухания этих отклонений они не дают. Эти и другие характеристики оцениваются отдельно. Функция 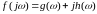представляет собой характеристический вектор, модуль и аргумент которого зависят от частоты 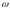. В Михайлов доказал, что САР будет устойчивой, если при изменении от 0 до 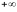вектор 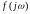повернётся в положительном направлении на угол, равный 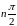или, что то же самое, если характеристическая кривая, описанная концом вектора , с ростом обходит последовательно в положительном направлении (без пропусков) n квадрантов (n – степень характеристического уравнения)

Х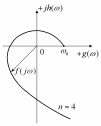 арактеристическая кривая (годограф) критерия А.В. Михайлова для устойчивой системы регулирования при степени характеристического уравнения n=4.

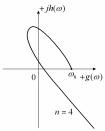
Характеристическая кривая (годограф) критерия А.В. Михайлова для неустойчивой системы регулирования при степени характеристического уравнения n=4.

Кроме того разработан и используется частотный критерий устойчивости Найквиста-Михайлова. Пусть разомкнутая система регулирования описывается некоторым уравнением: ,

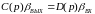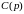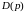где и – полиномы от p. В реальных САР степень полинома выше степени полинома или в крайнем случае равна ей. Характеристическое уравнение рассматриваемой разомкнутой системы: . Китерий устойчивости Найквиста-Михайлова сформулирован следующем виде: если степень полинома в равенстве выше степени полинома и соответствующая разомкнутая САР устойчива, то для ее устойчивости в замкнутом состоянии необходимо и достаточно, чтобы амплитудно-фазовая характеристика, описанная концом вектора 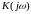при изменении угловой частоты от до 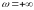, не охватывала точки M с координатами (-1, j0) на комплексной плоскости.

Условие устойчивости разомкнутой системы в общем случае можно определить по знакам корней полинома . При этом система будет устойчивой, если характеристическое уравнение не содержит корней с положительной вещественной частью.