4.3 Восстановление непрерывных сигналов

При дискретизации по времени функция непрерывного аргумента x(t) преобразуется в функцию дискретного аргумента x(t_k). Переход x(t) x(t_k) осуществляется путем взятия отсчетов функции x(t) в определенные дискретные моменты времени t_k, k=1,2,3,…В результате функция x(t) заменяется совокупностью мгновенных значений x(t_k). По этим мгновенным значениям можно восстановить исходную непрерывную функцию с заданной точностью. Функцию, полученную в результате восстановления по дискретным отсчетам x(t_k), называют воспроизводящей.

При дискретизации непрерывной функции приходится решать вопрос о том, как часто необходимо производить отсчеты функции, то есть каков должен быть шаг дискретизации .

При малых величинах количество отсчетов функции на отрезке обработки [0, T] будет большим и точность воспроизведения – высокой. При больших количество отсчетов уменьшится, но при этом снизится и точность воспроизведения. Обычно задается допустимая погрешность воспроизведения исходной функции. Оптимальной является такая дискретизация, которая обеспечивает представление исходной функции с заданной точностью минимальным количеством отсчетов x(t_k). В этом случае все отсчеты существенны для восстановления исходной функции. В случае неоптимальной дискретизации, кроме существенных, производятся и избыточные отсчеты.

4.3.1 Теорема Котельникова

Качество способа дискретизации, согласно которому отбираются отсчеты, оценивают по той ошибке, с которой удается воспроизвести исходную функцию.

К группе критериев отбора отсчетов относят такие модели сигнала и такие способы его воспроизведения, для которых ошибку воспроизведения удается обратить в нуль или близкое к нулю значение. Рассмотрим частотный критерий В.А. Котельникова, согласно которому интервалы между отсчетами выбираются с учетом частотного спектра дискретизируемого сигнала.

Если непрерывная функция f(t) удовлетворяет условиям Дирихле (ограничена, кусочно-непрерывна и имеет конечное число экстремумов) и ее спектр ограничен некоторой граничной частотой, называемой частотой среза , то существует такой максимальный шаг дискретизации (интервал между дискретными отсчетами), при котором имеется возможность безошибочного восстановления дискретизируемой функции по ее дискретным отсчетам. Этот максимальный интервал равен:

. (2)

Воспроизводящая функция при этом принимает вид бесконечного ряда, называемого рядом Котельникова:

. (3)

Таким образом, непрерывная функция f(t) представляется суммой произведений двух сомножителей, один из которых равен значению функции в дискретной точке, то есть , а другой является некоторой функцией времени, называемой функцией отсчетов:

. (4)

Свойства функции отсчетов:

1) В момент времени функция отсчета достигает своего наибольшего значения, равного единице (рисунок 5):

;

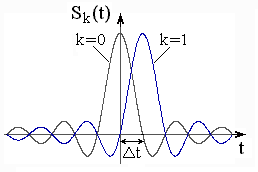
Рисунок 5 – Функции отсчетов при k = 0 и k = 1

2) в моменты времени, кратные , то есть при , где - любое целое число, функция отсчетов обращается в нуль:

.

3) функции отсчетов с различными номерами ортогональны на бесконечно большом интервале времени.

Величина интервала времени между дискретными отсчетами функции должна удовлетворять требованию теоремы Котельникова . Иными словами, для того, чтобы восстановление непрерывной функции по ее дискретным отсчетам было возможно с заданной точностью, необходимо, чтобы частота дискретизации была, по крайней мере, в два раза больше наивысшей частоты, присутствующей в спектре дискретизируемой функции. В противном случае неизбежны наложение частот (наложение верхних частот на нижние) (рисунок 6) и искажения при восстановлении непрерывной функции.

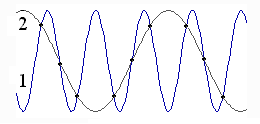
Рисунок 6 – Наложение верхних частот (кривая 1) на нижние частоты (кривая 2)

Теорема Котельникова сыграла большую роль в технике передачи и приема информации. Она позволила заменить исследование передачи непрерывных сообщений более простыми задачами исследования передачи дискретных сообщений.

В последние годы при изучении свойств сигналов на первый план стали выдвигать их способность быть носителями сообщений. Сообщения по своей природе относятся к случайным явлениям, и, таким образом, сигнал может служить переносчиком сообщения лишь в том случае, когда представляющая его непрерывная функция недетерминирована, случайна. Кроме того, реальные сигналы, являющиеся носителями информации, имеют начало и конец, то есть непрерывные функции, описывающие такие сигналы, имеют конечную длительность. Но такие функции не могут обладать ограниченным спектром. Между тем теорема Котельникова является точной лишь для функций с ограниченным спектром.

На практике использование теоремы Котельникова также наталкивается на ряд трудностей.

В первую очередь следует отметить, что представление непрерывной функции в виде дискретных отсчетов через промежуток времени не позволяет воспроизводить процесс, развивающийся во времени. Пусть, например, на интервале Т непрерывная функция времени восстанавливается по своим отсчетам. Если теперь вне интервала получен хотя бы один дополнительный отсчет, то при восстановлении изменяется вся непрерывная функция на всем предшествующем интервале Т. Таким образом, получение новых данных изменяет непрерывную функцию в «прошлом».

Наконец, для реальных сигналов граничная частота среза является неопределенным параметром, для выбора которого не существует достаточно обоснованных критериев.

Приведенные замечания свидетельствуют, что применение теоремы Котельникова вызывает определенные трудности в том случае, когда она рассматривается как точное утверждение. Практически, однако, идеально точное восстановление функции никогда не требуется, необходимо лишь ее воспроизведение с определенной, фиксированной точностью. Поэтому теорему Котельникова для функций с неограниченным спектром можно рассматривать как приближенную.