Н.Н.КЛЕВАНСКИЙ
КОМБИНАТОРНЫЕ ЗАДАЧИ В ПРОГРАММИРОВАНИИ
Конспект лекций
Саратов
1999 г.
1.АЛГОРИТМЫ НА ГРАФАХ
1.1.Машинное представление графов
Теорию
графов начали разрабатывать для решения
геометрических задач
(рис1.1), в
которых было несущественно, соединены
ли точки конфигурации отрезками прямых
или криволинейными дугами, какова длина
линий и другие геометрические
характеристики конфигурации. Важно
лишь то, что каждая линия соединяет
какие-либо две из заданных точек. Таким
образом, можно дать определение графа
как совокупности двух множеств V
(точек) и
E
(линий),
между элементами которых определено
отношение инцидентности, причем каждый
элемент
инцидентен ровно двум элементам
.
Элементы множества V
называются вершинами графа G,
элементы множества E
– его ребрами. В некоторых задачах
инцидентные ребру вершины неравноправны
и рассматриваются в определенном
порядке. Тогда каждому ребру можно
приписать направление от первой из
инцидентных вершин ко второй. Граф в
этом случае называется ориентированным
по сравнению с ранее определенным
неориентированным.
Первые исследования геометрических объектов с помощью графов принадлежат Эйлеру, оттуда же его формулы
F – A + S = 2 для тела F – A + S = 1 для замкнутой поверхности
В
теории графов классическим способом
представления графа служит матрица
инциденций (табл.1.1). Это матрица А с n
строками, соответствующими вершинам,
и m
столбцами, соответствующими ребрам.
Для ориентированного графа столбец,
соответствующий дуге
,
содержит –1 в строке, соответствующей
вершине x,
1 – в строке, соответствующей вершине
y,
и 0 во всех остальных строках. В случае
неориентированного графа столбец,
соответствующий ребру
содержит 1 в строках, соответствующих
x
и y,
и нули в
остальных строках.
Табл.1.1.Матрицы инциденций неориентированного и ориентированного графов (рис.1.1)
Неориентированный граф |
||||||||||||
|
{1,2} |
{1,4} |
{1,7} |
{2,3} |
{2,6} |
{3,4} |
{3,5} |
{3,6} |
{4,5} |
{5,6} |
{5,7} |
{6,7} |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
6 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
7 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
Ориентированный граф |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
-1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
3 |
0 |
1 |
-1 |
-1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
0 |
0 |
0 |
0 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
0 |
5 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
-1 |
-1 |
0 |
0 |
0 |
6 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
-1 |
-1 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
-1 |
С
алгоритмической точки зрения матрица
инциденций является, вероятно, самым
худшим способом представления графа,
который только можно представить.
Во-первых, он требует nm
ячеек памяти, большинство из которых
занято нулями. Неудобен также доступ к
информации. Лучшим способом представления
графа является матрица смежности
(табл.1.2), определяемая как матрица В
размера n
n,
в которой
если существует ребро, идущее из вершины
x
в вершину y,
и
в противном случае. Для неориентированного
графа важен факт наличия ребра, что
приводит к симметричности матрицы
смежности.
Табл.1.2.Матрицы смежности неориентированного и ориентированного графов (рис.1.1)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
2 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
|
0 |
0 |
0 |
1 |
0 |
3 |
0 |
1 |
|
1 |
1 |
1 |
0 |
|
3 |
0 |
1 |
|
1 |
0 |
0 |
0 |
4 |
1 |
0 |
1 |
|
1 |
0 |
0 |
|
4 |
0 |
0 |
0 |
|
0 |
0 |
0 |
5 |
0 |
0 |
1 |
1 |
|
1 |
1 |
|
5 |
0 |
0 |
1 |
1 |
|
0 |
0 |
6 |
0 |
1 |
1 |
0 |
1 |
|
1 |
|
6 |
0 |
0 |
1 |
0 |
1 |
|
0 |
7 |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
7 |
0 |
0 |
0 |
0 |
1 |
1 |
|
Основным преимуществом матрицы смежности является возможность за один шаг получить ответ на вопрос «существует ли ребро из x в y?» Недостаток – объем памяти n2 независимо от числа ребер. Более экономным в отношении памяти является метод представления графа с помощью списка пар вершин, соответствующих его ребрам. Для обоих графов (рис.1.1) такой список будет иметь вид.
Табл.1.3.Список ребер, соответствующий графам рис.1.1.
2 1 |
2 3 |
3 5 |
3 6 |
4 1 |
4 3 |
4 5 |
5 6 |
5 7 |
6 2 |
6 7 |
7 1 |
Объем памяти 2m. Неудобством является большое число шагов – порядка m в худшем случае, - необходимое для получения множества вершин, к которым ведут ребра из данной вершины. Ситуацию можно значительно улучшить, упорядочив множество пар лексикографически и применяя двоичный поиск, но лучшим решением во многих случаях оказывается структура данных следующего вида.
1: 2, 4, 7 1: 2: 1, 6, 3 2: 1, 3 3: 2, 6, 5, 4 3: 5, 6 а) 4: 1, 3, 5 б) 4: 1, 3, 5 5: 3, 6, 7, 4 5: 6, 7 6: 2, 7, 5, 3 6: 2, 7 7: 1, 5, 6 7: 1 Рис.1.2.Списки инцидентности неориентированного (а) и ориентированного (б) графов (рис.1.1). |
Так как данная форма представления связана с кольцевыми структурами, то введем спецификацию кольцевого списка для номеров вершин, представляемых целыми числами, а затем спецификацию графа, как массива кольцевых структур.
Circ = data type [int] is create, element, change, delete, insert, size
Описание Кольцевые списки circ - изменяемые однонаправленные кольцевые списки целых чисел. Операции delete и insert модифицируют списки. Кольцевой список имеет заголовочную часть, содержащую центральный элемент и ссылку на текущий элемент списка.
Операции
create = proc() returns(circ[int]) effects возвращает новый, пустой кольцевой список
element = proc(r:circ[int]) returns(int) requires r создан и не пуст effects возвращает текущий элемент кольцевого списка
change = proc(r:circ[int]) requires r создан и не пуст effects переустанавливает ссылку заголовочной части на следующий элемент кольцевого списка r, который становится текущим
delete = proc(r:circ[int]) requires r создан и не пуст modifies r effects удаляет текущий элемент кольцевого списка r и переустанавливает ссылку заголовочной части на следующий после удаляемого элемент
insert = proc(r:circ[int], x:int) requires r создан modifies r effects вставляет x в r перед текущим элементом и переустанавливает ссылку заголовочной части на элемент x
size = proc(r:сirc[int]) returns(int) requires r создан effects возвращает число элементов кольцевого списка r, если он пуст, то возвращает 0
end circ
|
Рис.1.3.Спецификация параметризованной абстракции данных для кольцевых списков.
Graph = data type [circ] is create, empty, fetch, store
Описание
Массивы graph – массивоподобные линейные списки кольцевых списков circ целых чисел
Операции
create = proc (n:int) returns (graph) effects возвращает новый пустой массив
empty = proc (g:graph) returns (bool) requires g существует effects возвращает значение true, если массив g не содержит элементов, в противном случае – false
fetch = proc (g:graph; i:int) returns (circ) signals (bounds) effects если i < 0 или i > n, то сигнализирует через bounds, иначе возвращает элемент g с индексом i
store = proc (g:graph; i:int; elem:circ) signals (bounds) modifies g effects если i < 0 или i > n, то сигнализирует через bounds, иначе присваиает elem значение элемента g с индексом i
end graph
|
Рис.1.4.Спецификация графа как «массива» кольцевых структур.
Графическая интерпретация введенных типов данных представлена на рис.1.5.
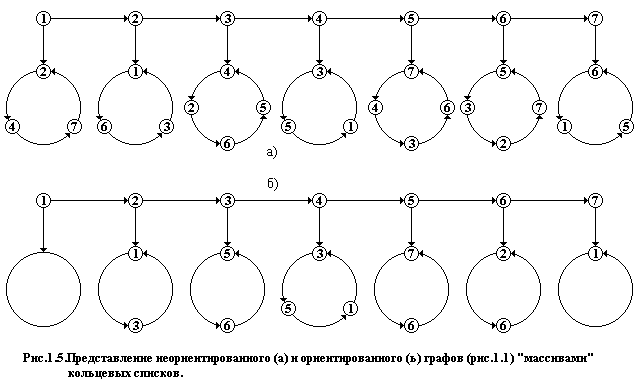
1.2.Поиск в глубину в графе
Существует много алгоритмов на графах, в основе которых лежит систематический перебор вершин графа, такой, что каждая вершина просматривается в точности один раз. Поэтому важной задачей является нахождение хороших методов поиска в графе. вообще говоря, метод поиска «хорош», если
он позволяет алгоритму решения задачи легко «погрузиться» в этот метод;
каждое ребро графа анализируется не более одного раза (или, что существенно не меняет ситуации, число раз, ограниченное константой).
Одной из основных методик проектирования графовых алгоритмов является поиск в глубину (depth first search) в неориентированном графе. Общая идея этого метода состоит в следующем. Пусть поиск начинается с некоторой фиксированной вершины vo. Затем выбирается произвольная вершина u, смежная с vo, после чего процесс повторяется от u. В общем случае можно положить, что процесс подошел к вершине v. Если существует еще не просмотренная вершина u (u-v), то она рассматривается и, начиная с нее, продолжается поиск. Если же не существует ни одной не просмотренной вершины, смежной с v, то полагается, что вершина v использована, и осуществляется возврат в вершину, из которой попали в v, и процесс продолжается. Если v = vo, то поиск завершается.
Это может быть специфицировано следующей рекурсивной процедурой.
WG = proc (u:int; g:graph; НОВЫЙ: array of bool) modifies НОВЫЙ effects 1. “рассмотреть” вершину u 2. НОВЫЙ[u] = false 3. c=graph.fetch(g,u) 4. i = circ.size (c) 5. пока i > 0 5.1. j = circ.element (c) 5.2. если НОВЫЙ[j], то WG(j), иначе circ.change (c) 5.3 i = i-1
|
Рис.1.6.Процедурная спецификация вспомогательной процедуры для поиска в глубину.
Теперь поиск в глубину в произвольном, не обязательно связном графе, может быть специфицирован следующим образом.
Depth = proc (g:graph) effects 1. для i = 1 до n выполнить НОВЫЙ [i] = true 2. для i = 1 до n выполнить если НОВЫЙ [i], то WG(i)
|
Рис.1.7.Спецификация процедуры поиска в глубину.
Полученный алгоритм просматривает каждую вершину в точности один раз и его сложность порядка O(n + m), то есть не более n + m. Следует также отметить, что алгоритм поиска в глубину в произвольном графе можно легко модифицировать так, чтобы он вычислял связные компоненты этого графа.
В связи с тем, что поиск в глубину играет важную роль в проектировании алгоритмов на графах, представим также нерекурсивную версию процедуры WG. Рекурсия устраняется стандартным способом при помощи стека (рис.1.8). Каждая просмотренная вершина помещается в стек и удаляется из стека после использования (рис.1.9).
Stack = data type [t:type] is new, is_empty, top, pop, push
Описание Тип данных stack используется для хранения элементов t. Элементы могут извлекаться из стека или добавляться в него только по методу LIFO (Last Input - First Output)
Операции
function new:stack[t] effects возвращает новый стек, без элементов в нем
function is_empty(s:stack[t]):boolean effects возвращает значение true, если в стеке s нет элементов, в противном случае возвращает значение false
function top(s:stack[t]):t requires s создан и не пуст effects возвращает значение начального элемента стека s
pop = proc(s:stack[t], e:t) requires s создан и не пуст modifies s effects добавляет элемент e в начало стека s
function push(s:stack[t]):t requires s создан и не пуст modifies s effects возвращает значение элемента из начала стека s и удаляет этот элемент из стека
end stack
|
Рис.1.8.Спецификация параметризованной абстракции данных для стека.
WG1 = proc (u:int; g:graph; НОВЫЙ: array of bool) modifies НОВЫЙ effects 1. s = stack.new( ); stack.pop(s,u); «рассмотреть» вершину u; НОВЫЙ[u] = false 2. пока (not stack.is_empty(s)) выполнять 2.1. t = stack.top(s); c = graph.fetch(g,t) 2.2. если circ.size(c) = 0, то b = false иначе b = not НОВЫЙ[circ.element(c)] 2.3. пока b выполнять 2.3.1. circ.change(c); t1 = circ.element; c = graph.fetch(g,t1) 2.3.2. если circ.size(c) = 0, то b = false иначе b = not НОВЫЙ[circ.element(c)] 2.4. если circ.size(c)<>0, то 2.4.1. t = circ.element(c) 2.4.2. stack.pop(s,t) 2.4.3. НОВЫЙ[t] = false иначе t = stack.push(s)
|
Рис.1.9.Процедурная спецификация нерекурсивной процедуры для поиска в глубину.
На рис.1.10.а показан граф, вершины которого перенумерованы (значения в скобках) в соответствии с тем порядком, в котором они просматриваются в процессе поиска в глубину. Предполагается, что номера вершин в списках инцидентности этого графа были упорядочены по возрастанию. На рис.1.10.б продемонстрирована аналогичная перенумерация для неориентированного графа, представленного на рис.1.1.б.
