2.8. Граничные условия в задаче о продольном сдвиге

В задаче о продольном сдвиге ячейка периодичности находится в антиплоском деформированном состоянии:

(2.8.1)

В данной задаче неинвариантными относительно преобразований могут быть только компоненты:

2.8.1. Анализ кинематических граничных условий Хашина – Розена. Граничные условия имеют вид:

(2.8.2)

;

– рассматривается продольный сдвиг в плоскости .

Преобразование преобразует ячейку периодичности, находящуюся под влиянием внешнего воздействия (2.8.2), в саму себя. Используя таблицы инвариантности 2.3 и 2.2, выписываем результаты применения преобразования :

;

– V₂: неинвариантность компонента u₃ вектора перемеще­ния u не противоречит кинематической совместности, так как 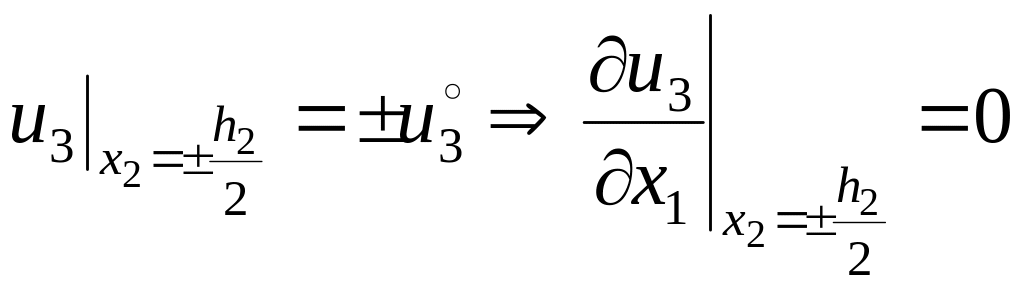– прямолинейные ребра сопряжения остаются прямолинейными ребрами в деформированной ячейке периодичности (поворот ребер исключен в

силу принципа суперпозиции Кюри).

– t₃₁: касательное напряжение терпит разрыв при пе­реходе через плоскости сопряжения , так как для гетерогенной ячейки периодичности, находящейся под влиянием внешнего воздействия (2.8.2), не является нулевым:

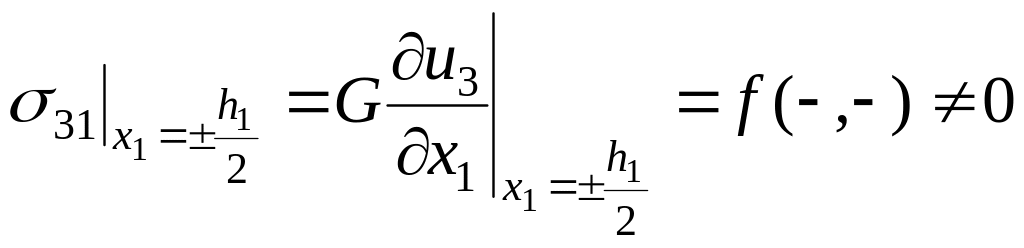
Вывод:

кинематические граничные условия Хашина – Розена не удовлетворяют условию статической совместности деформированных ячеек периодичности.

2.8.2. Анализ статических граничных условий Хашина – Розена. Граничные условия имеют вид:

(2.8.3)

;

;

;

– V₃: неинвариантность компонента u₃ относительно пре­образования противоречит условиям кинематической совместности, так как

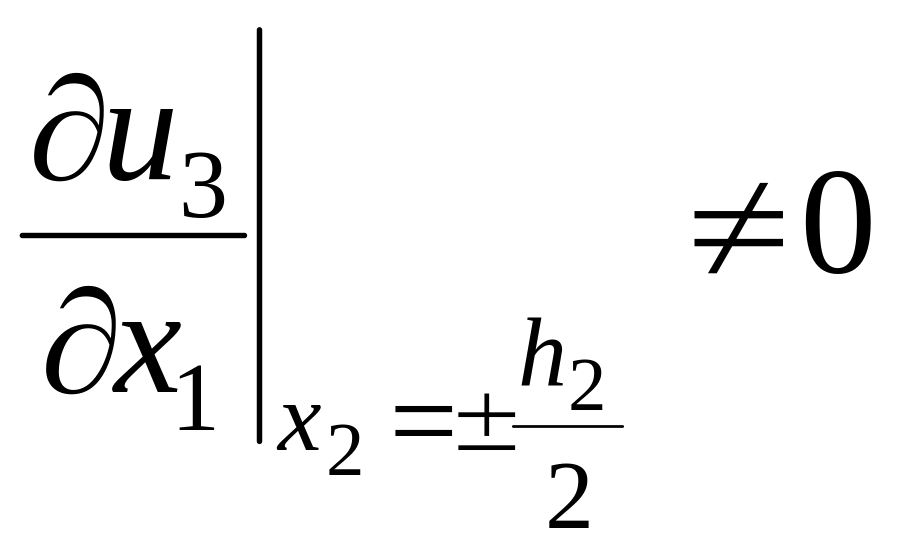– прямолинейные ребра сопряжения не остаются прямолинейными ребрами в деформированной гетерогенной ячейке перио­дичности;

– t₃₁: неинвариантность касательного напряжения не противоречит условию статической совместности, так как из граничных условий следует:

.

Вывод: статические граничные условия Хашина – Розена не удовлетворяют условию кинематической совместности деформированных ячеек периодичности.

2.8.3. Синтез смешанных граничных условий. При помощи алгоритма 2.5.3 сформируем граничные условия в задаче о про­дольном сдвиге ячейки периодичности, которые удовлетворяют условиям кинематической и статической совместности деформированных ячеек периодичности.

1. Результаты применения преобразования :

2. На плоскостях сопряжения задаем касательный компонент вектора перемещения u, являющийся неинвариантным относительно преобразования :

3. Полагаем равным нулю неинвариантное относительно преобразования касательное напряжение :

Вывод:

граничные условия в задаче о продольном сдвиге ячейки периодичности, удовлетворяющие кинемати­ческой и статической совместности деформированных ячеек периодичности, имеют вид:

;

;

;

– смешанные граничные условия.

2.9. Энергетические соотношения

2.9.1. Теорема о равенстве среднего упругого потенциала “эффективному” упругому потенциалу. В подпараграфе 1.3.3 были сформулированы и доказаны теоремы о равенстве средне­го по объему упругого потенциала “эффективному” упругому потенциалу при задании кинематических или статических грани­чных условий Хашина – Розена. В параграфах 2.6, 2.7, 2.8 сформированы новые граничные условия, удовлетворяющие условиям кинематической и статической совместности деформи­рованных ячеек периодичности – кинематико-статические граничные условия в задачах о поперечном растяжении и поперечном сдвиге, смешанные граничные условия в задаче о продольном сдвиге ячейки периодичности. Для новых граничных условий также имеет место

Теорема 3. Если для гетерогенной среды, занимающей объем и ограниченной поверхностью S

1. В задаче о поперечном растяжении (плоская деформация) заданы кинематико-статические граничные условия:

; (2.9.1)

;

2. В задаче о поперечном сдвиге (плоская деформация) заданы кинематико-статические граничные условия:

; (2.9.2)

;

3. В задаче о продольном сдвиге (антиплоская деформация) заданы смешанные граничные условия:

; (2.9.3)

;

;

соответствующие однородному напряженно-деформированному состоянию гомогенной среды, то средний по объему упругий потенциал равен “эффективному” упругому потенциалу:

(2.9.4)

(2.9.5)

(2.9.6)

а эффективные определяющие соотношения имеют вид:

(2.9.7)

2.9.2. Задача о поперечном растяжении. Докажем теорему в случае, когда на поверхности S , ограничивающей объем V, заданы кинематико-статические граничные условия (2.9.I).

1. Вычислим средний по объему упругий потенциал:

Учитывая граничные условия (2.9.1), получим:

Из свойства двоякой четности нормального напряжения следует: .

Выражение для среднего по объему V упругого потенциала принимает вид:

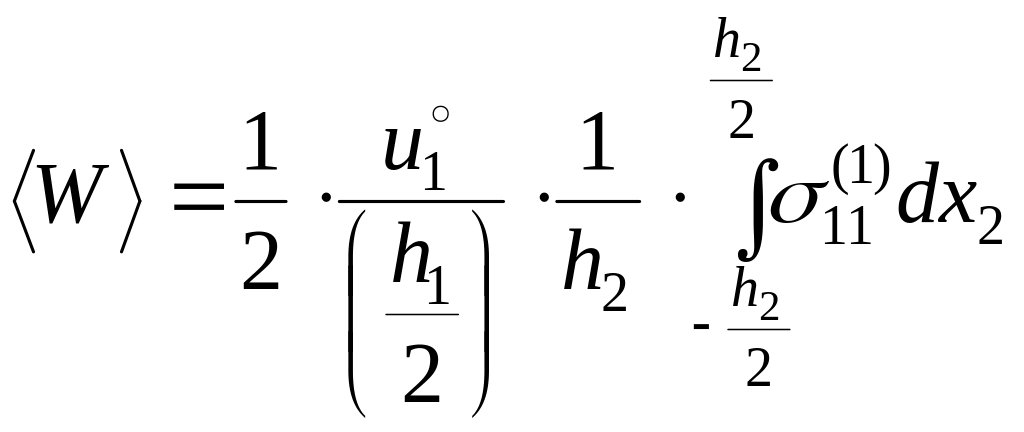(2.9.8)

2. Вычислим средний по объему V тензор деформаций:

Учитывая свойства четности–нечетности компонентов вектора перемещения , запишем выражение для среднего по объему тензора деформаций в следующем виде:

(2.9.9)

3. Вычислим средний по объему V тензор напряжений:

Из свойства двоякой четности нормальных напряжений следует:

.

Выражение для среднего по объему V тензора напряжений принимает вид:

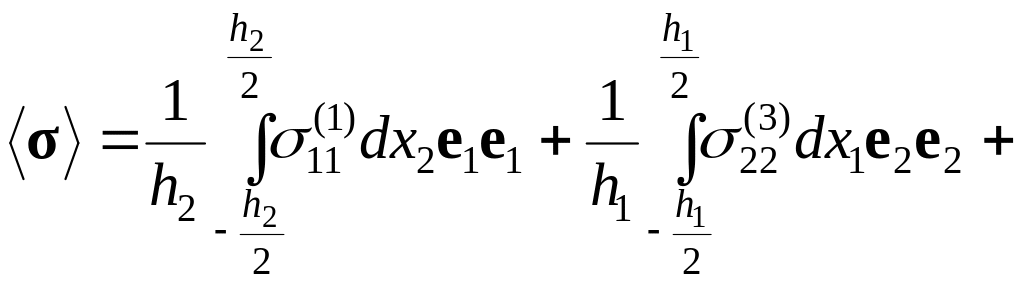
(2.9.10)

4. Определим “эффективный” упругий потенциал, используя выражения (2.9.9) и (2.9.10):

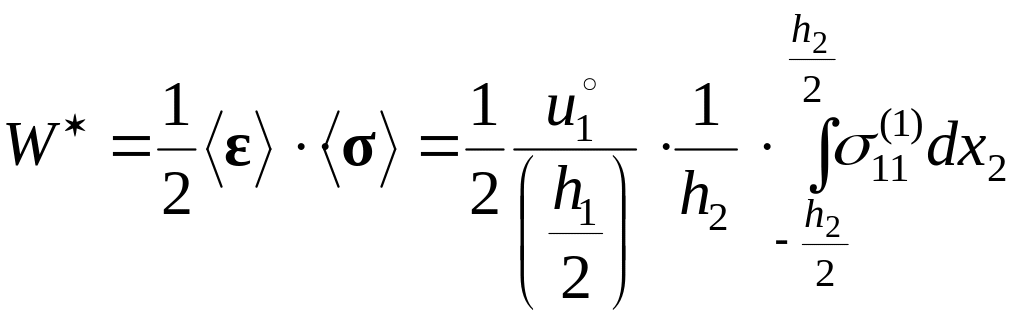(2.9.11)

Сравнив выражения (2.9.8) и (2.9.11), убеждаемся, что при задании кинематико-статических граничных условий (2.9.1) средний по объему V упругий

потенциал равен “эффек­тивному” упругому потенциалу.

2.9.3. Задача о поперечном сдвиге. Докажем теорему в случае, когда на поверхности S, ограничивающей объем V, заданы кинематико-статические граничные условия (2.9.2).

1. Вычислим средний по объему V упругий потенциал, уч­итывая граничные условия (2.9.2) и свойства двоякой четности касательного напряжения :

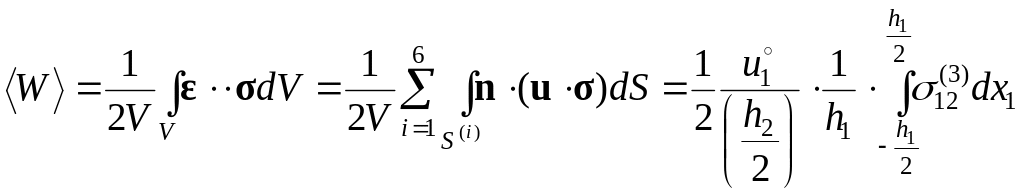(2.9.12)

2. Вычислим средний по объему V тензор деформаций, учитывая граничные условия (2.9.2) и свойства четности–нечетности компонентов вектора перемещения :

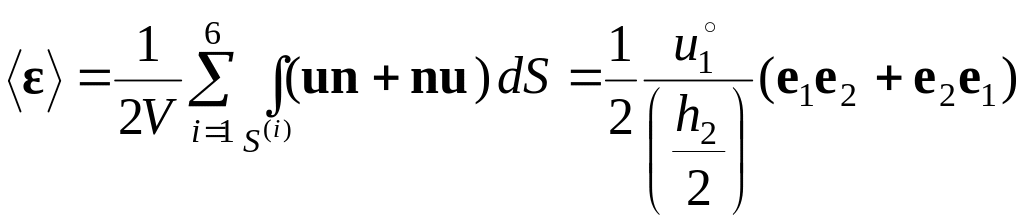(2.9.13)

3. Вычислим средний по объему V тензор напряжений, учитывая граничные условия (2.9.2) и свойства двоякой четности напряжений :

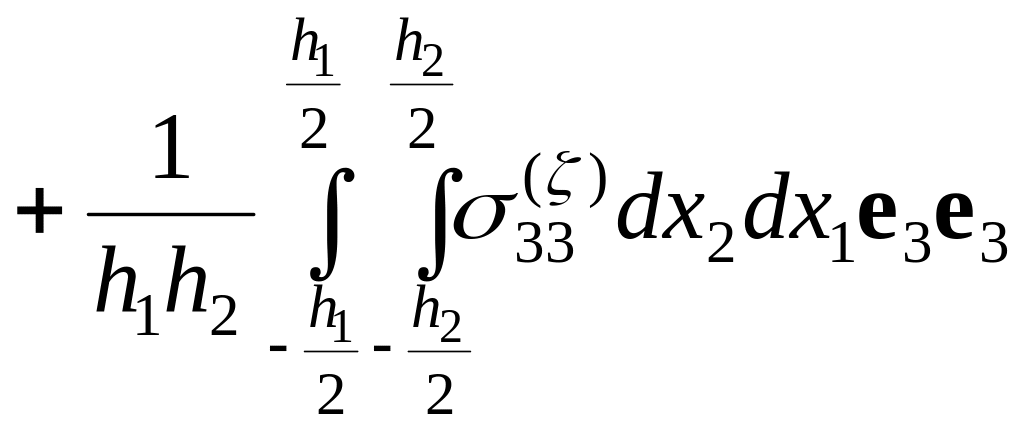
Учитывая условие обращения в нуль главного момента по­верхностных сил

запишем выражение для среднего по объему V тензора напря­жений в следующем виде:

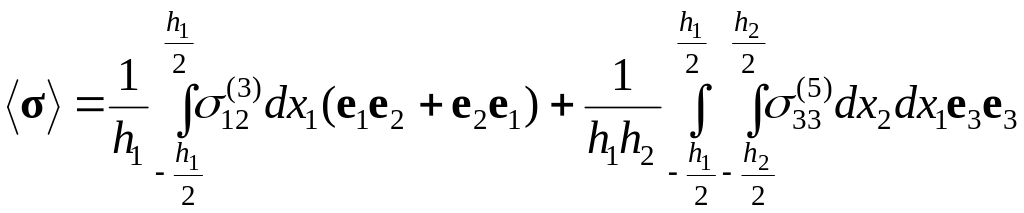(2.9.14)

4. Определим “эффективный” упругий потенциал, используя выражения (2.9.13), (2.9.14):

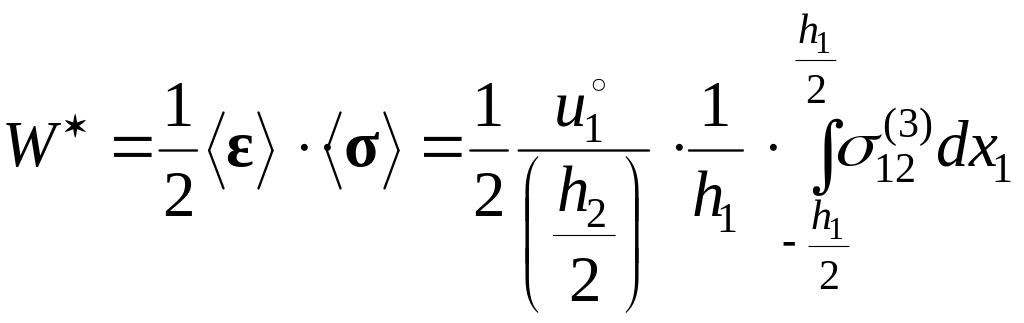(2.9.15)

Сравнив выражения (2.9.12) и (2.9.15), убеждаемся, что при задании кинематико-статических граничных условий (2.9.2) средний по объему V упругий потенциал равен “эф­фективному” упругому потенциалу.

2.9.4. Задача о продольном сдвиге. Докажем теорему в случае, когда на поверхности S, ограничивающей объем V , заданы смешанные граничные условия (2.9.3).

1. Вычислим средний по объему V упругий потенциал, учитывая граничные условия (2.9.З) и свойства двоякой четности касательного напряжения :

(2.9.16)

2. Вычислим средний по объему V тензор деформаций, учитывая граничные условия (2.9.3) и свойства четности-нечетности компонента вектора перемещения :

(2.9.17)

3. Вычислим средний по объему V тензор напряжений, учитывая граничные условия (2.9.3) и свойства двоякой четности–нечетности касательных напряжений , :

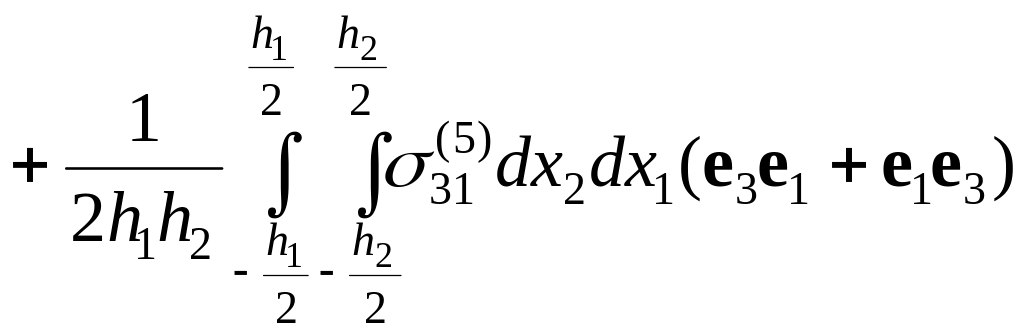
Учитывая условие обращения в нуль главного момента по­верхностных сил

,

запишем выражение для среднего по объему V тензора напря­жений в следующем виде:

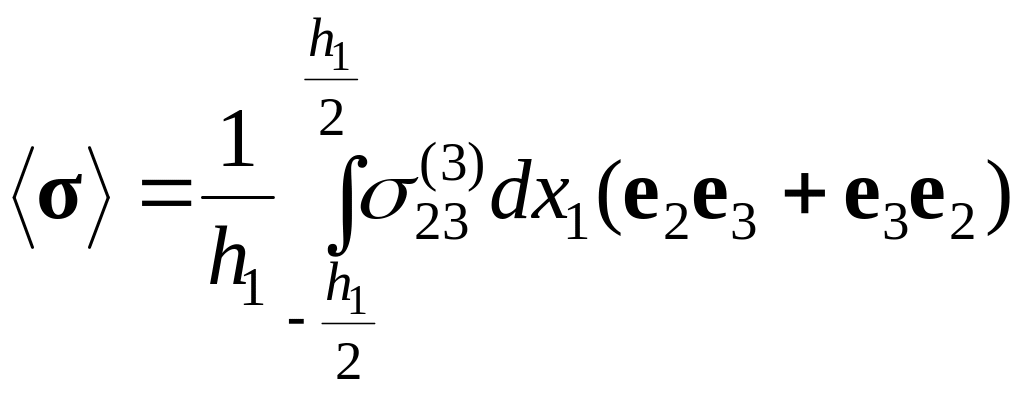(2.9.18)

4. Определим “эффективный” упругий потенциал, исполь­зуя выражения (2.9.17), (2.9.18):

(2.9.15)

Сравнив выражения (2.9.16) и (2.9.19), убеждаемся, что при задании смешанных граничных условий (2.9.3) средний по объему упругий потенциал равен “эффективному” упругому потенциалу.

Теорема доказана.