
- •Элементы теории поля
- •Скалярное поле и его характеристики
- •Производная скалярного поля по направлению.
- •Градиент скалярного поля.
- •Векторное поле и его характеристики: векторные линии, поток поля через поверхность
- •Поток векторного поля
- •Дивергенция и ротор
- •Найдём ротор поля скоростей :
- •Дифференциальные операции первого и второго порядков.
Элементы теории поля

![]()
![]()

Скалярное поле и его характеристики

![]()
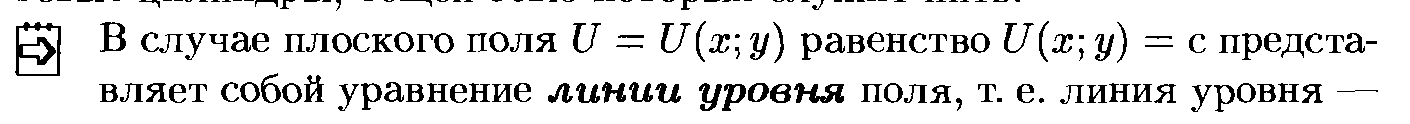
![]()
Производная скалярного поля по направлению.
Пусть в некоторой области пространства
задано скалярное поле
![]() .
Рассмотрим это поле в прямоугольной
декартовой системе координат
.
Рассмотрим это поле в прямоугольной
декартовой системе координат
![]() ,
,
![]() ,
,
![]() и зафиксируем точку
и зафиксируем точку
![]() .
Проведем через эту точку прямую в
направлении вектора
.
Проведем через эту точку прямую в
направлении вектора
![]() с началом в точке
и рассмотрим значения скалярной функции
в точке
и в близких к ней точках
с началом в точке
и рассмотрим значения скалярной функции
в точке
и в близких к ней точках
![]() .
Введем число
.
Введем число
![]() ,
равное длине вектора
,
равное длине вектора
![]() (
(![]() ),
если векторы
),
если векторы
![]() и
совпадают по направлению, и равное
и
совпадают по направлению, и равное
![]() ,
если эти векторы противоположны по
направлению.
,
если эти векторы противоположны по
направлению.
Определение. Производной
скалярной функции
в точке
![]() по
направлению вектора
называется предел
по
направлению вектора
называется предел
![]() ,
,
обозначаемый символом
![]() .
.
Вычисляется производная по направлению
 ,
,
где
![]() -
направляющие косинусы вектора l
-
направляющие косинусы вектора l
В частности, если вектор
![]() сонаправлен с одной из координатных
осей, то производная по направлению
совпадает с соответствующей частной
производной. Например, если
сонаправлен с одной из координатных
осей, то производная по направлению
совпадает с соответствующей частной
производной. Например, если
![]() ,
то
,
то
![]() .
.
Производная поля в точке
по направлению
характеризует скорость изменения поля
по направлению
,
а частные производные
![]() ,
,
![]() ,
,
![]() – скорость изменения скалярного
поля
– скорость изменения скалярного
поля
![]() по направлению осей
по направлению осей
![]() ,
,
![]() ,
,
![]() соответственно.
соответственно.
Градиент скалярного поля.
Определение. Градиентом
скалярного поля
![]() в точке
в точке
![]() называется вектор, обозначаемый
называется вектор, обозначаемый
![]() .
.
Вектор
![]() указывает направление наискорейшего
возрастания функции
указывает направление наискорейшего
возрастания функции
![]() в точке
стороны,
в точке
стороны,
![]() ,
вектор
,
вектор
![]() указывает на направление наискорейшего
убывания функции
в точке
.
указывает на направление наискорейшего
убывания функции
в точке
.
Векторное поле и его характеристики: векторные линии, поток поля через поверхность


Поток векторного поля
Рассмотрим
физический смысл потока векторного
поля (поверхностного интеграла второго
рода). Пусть в некоторой области
![]() евклидова пространства
евклидова пространства
![]() течет со скоростью
течет со скоростью
![]() жидкость,
имеющая объемную плотностью
жидкость,
имеющая объемную плотностью
![]() .
Вычислим количество жидкости протекающей
через некоторую гладкую поверхность
.
Вычислим количество жидкости протекающей
через некоторую гладкую поверхность
![]() ,
расположенную в области
.
Для этого ориентируем
единичным вектором нормали
,
расположенную в области
.
Для этого ориентируем
единичным вектором нормали
![]() и разобьем поверхность на части
и разобьем поверхность на части
![]() ,
,
![]() столь малого диаметра, чтобы они
практически не отличались от своих
плоских площадок. Пусть
столь малого диаметра, чтобы они
практически не отличались от своих
плоских площадок. Пусть
![]() одна из таких частей с единичным вектором
нормали
одна из таких частей с единичным вектором
нормали
![]() .
Тогда через
в направлении нормали
протечет в единицу времени
.
Тогда через
в направлении нормали
протечет в единицу времени
![]() жидкости, где
жидкости, где
![]() – площадь части
.
Это выражение для количества
– площадь части
.
Это выражение для количества
![]() жидкости будет тем точнее, чем меньше
диаметр
.
Заметим, что
будет положительным, если жидкость
течет через
в направлении вектора
и отрицательным – в противоположном
случае. Общее количество
жидкости будет тем точнее, чем меньше
диаметр
.
Заметим, что
будет положительным, если жидкость
течет через
в направлении вектора
и отрицательным – в противоположном
случае. Общее количество
![]() жидкости, протекающей через поверхность
,
приблизительно равно
жидкости, протекающей через поверхность
,
приблизительно равно
![]() .
.
Переходя
к пределу в этом выражении при
![]() ,
где
,
где
![]() – максимальный диаметр частей
,
,
находим
– максимальный диаметр частей
,
,
находим
![]() .
(4.3.10)
.
(4.3.10)
Формула
(4.3.10) определяет поток (количество)
жидкости через выбранную сторону
поверхности
,
заданную вектором
![]() ,
и физический смысл поверхностного
интеграла второго рода.
,
и физический смысл поверхностного
интеграла второго рода.
Если
![]() – поле сил, то говорят, что поток
векторного поля
– поле сил, то говорят, что поток
векторного поля
![]() ,
,
равен количеству силовых (векторных) линий, пронизывающих в единицу времени поверхность в направлении .
