
- •Задача линейного программирования в общем виде.
- •Виды злп и способы перехода от одного вида к другому.
- •Основные теоремы линейного программирования.
- •Симплекс-метод.
- •Задача об использовании сырья
- •Метод искусственного базиса.
- •Алгоритм метода искусственного базиса.
- •Двойственность задач линейного программирования. Таблица соответствий.
- •Теоремы двойственности.
- •Критерии оптимальности.
- •Транспортная задача. Закрытая и открытая модели.
- •Теорема о существовании оптимального решения.
- •Целочисленные злп, графический метод решения в случае двух переменных.
- •Задачи о назначениях и о коммивояжере как частные случаи целочисленных злп.
- •Метод ветвей и границ.
- •Алгоритм метода ветвей и границ:
- •Стандартная задача нелинейного программирования.
- •Локальный экстремум. Необходимое и достаточное условия.
Теоремы двойственности.
Рассмотрим стандартную задачу ЛП и двойственную к ней:
Таблица 37.1
-
Прямая задача (I)
Двойственная ей задача (II)
………………………
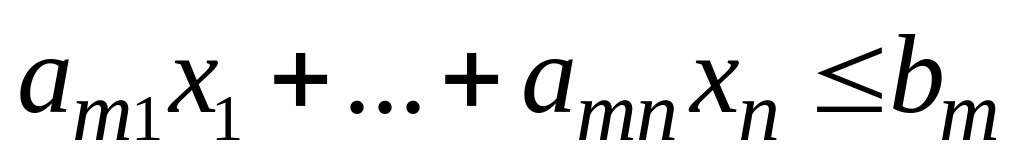
………
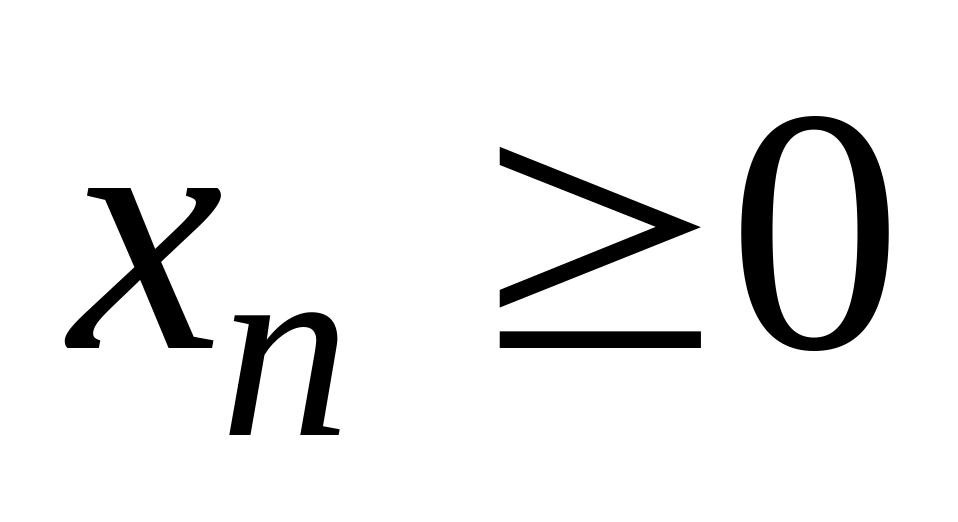
………
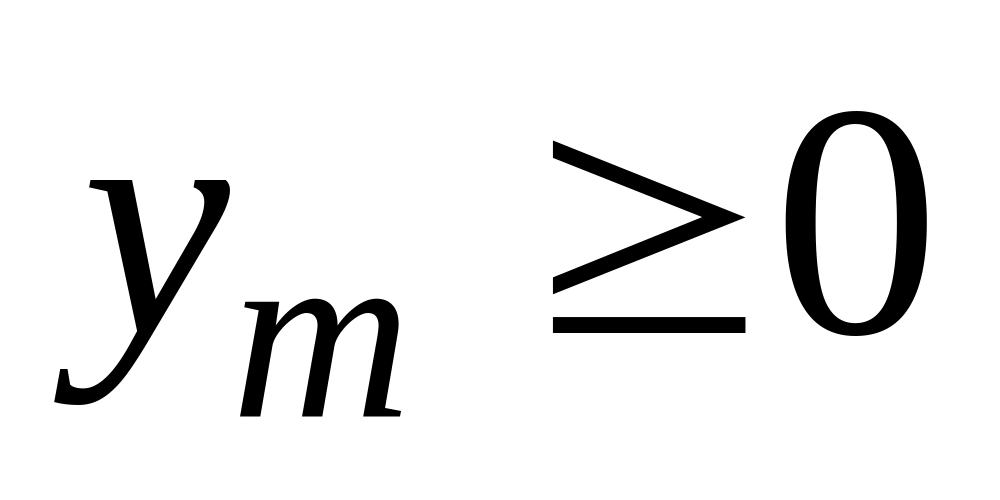
……………………………..
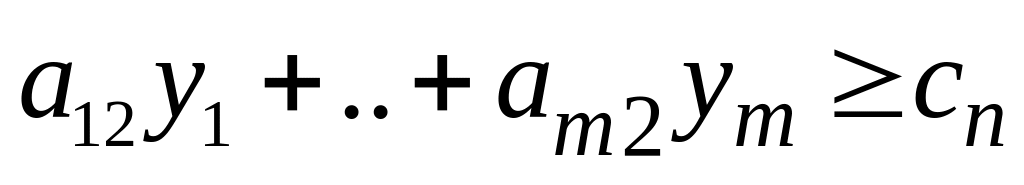
Пара двойственных задач (I) и (II) называется парой симметрических двойственных задач.
Не ограничивая общности, теорию двойственности можно рассматривать для пары симметрических задач, поскольку для любой задачи ЛП существует эквивалентная ей стандартная задача ЛП и поэтому теоремы, справедливые для пары симметрических двойственных задач, будут справедливы для пары общих двойственных задач.
Рассмотрим пару симметрических двойственных задач в матричной форме записи.
Таблица 37.2.
Прямая задача (I) |
Двойственная ей задача (II) |
|
|
Здесь
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
матрица из
-
матрица из
![]() строк и
строк и
![]() столбцов,
столбцов,
![]() -
транспонированная матрица. Введем
обозначения для допустимых областей
задачи (I) и (II).
-
транспонированная матрица. Введем
обозначения для допустимых областей
задачи (I) и (II).
![]() ,
,
![]()
Основное
неравенство двойственности:
для
любых допустимых решений прямой задачи
![]() и для любых допустимых решений двойственной
задачи
и для любых допустимых решений двойственной
задачи
![]() выполняется неравенство
выполняется неравенство ![]() .
.
Следствие
(достаточное
условие оптимальности):
если
для некоторых допустимых решений
![]() и
и ![]() выполняется равенство значений целевых
функций
выполняется равенство значений целевых
функций
![]() ,
то
,
то
![]() ,
,
![]() -
оптимальные решения задачи (I) и (II)
соответственно.
-
оптимальные решения задачи (I) и (II)
соответственно.
Первая теорема двойственности: если одна из пары двойственных задач (I) и (II) разрешима, то разрешима и другая задача, причем оптимальные значения целевых функций прямой и двойственной задач совпадают.
![]() ,
(37.1)
,
(37.1)
где
![]() ,
,
![]() оптимальные
планы задач (I) и (II) соответственно.
оптимальные
планы задач (I) и (II) соответственно.
Вторая теорема
двойственности:
чтобы
допустимые решения
,
![]() пары двойственных задач (I) и (II) были
оптимальными необходимо и достаточно,
чтобы выполнялись условия:
пары двойственных задач (I) и (II) были
оптимальными необходимо и достаточно,
чтобы выполнялись условия:
1)
![]() ,
(37.2)
,
(37.2)
2)
![]() .
(37.3)
.
(37.3)
Критерии оптимальности.
Первый критерий
оптимальности:
Решение
оптимально
тогда и только тогда, когда существует
решение
![]() такое,
что
такое,
что
![]() .
(38.1)
.
(38.1)
Второй критерий оптимальности: чтобы допустимые решения , - пары двойственных задач (I) и (II) были оптимальны, необходимо и достаточно, чтобы выполнялись соотношения:
если
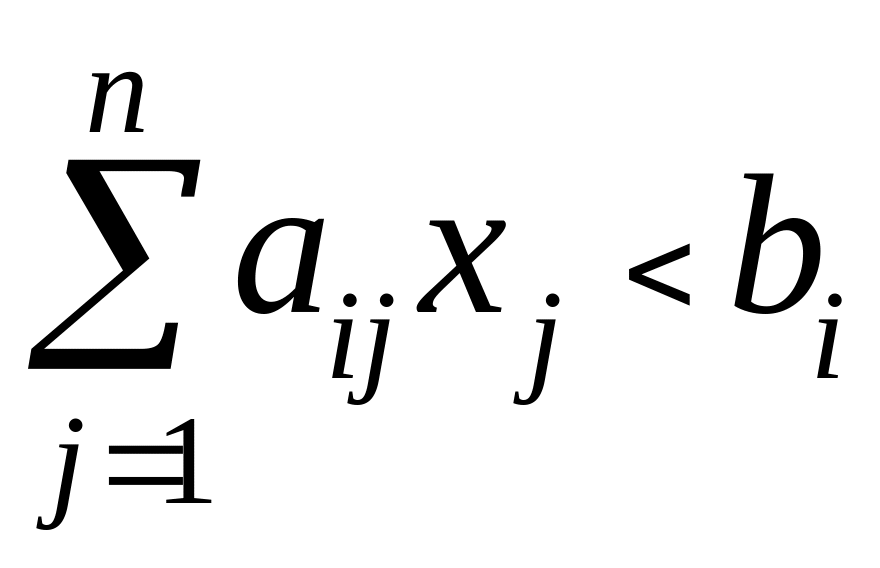 ,
то
,
то
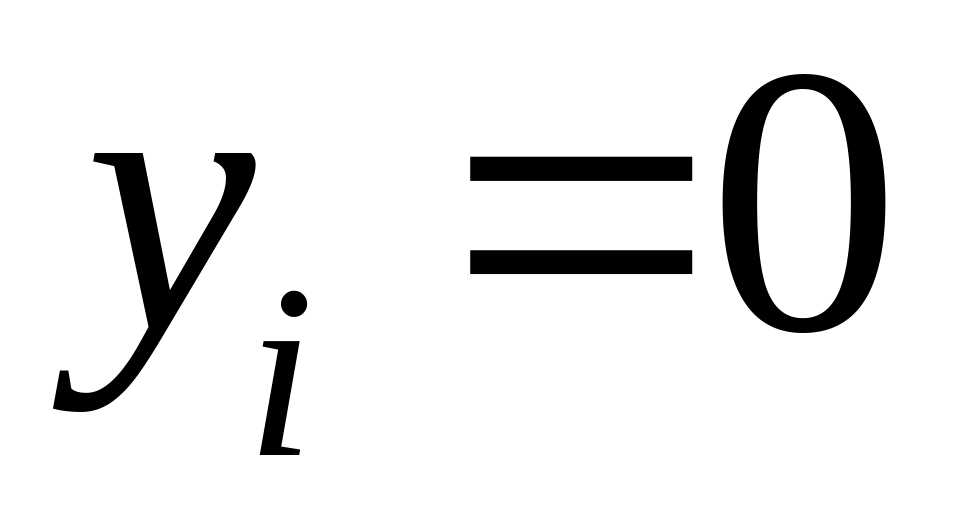 ;
(38.2)
;
(38.2)если
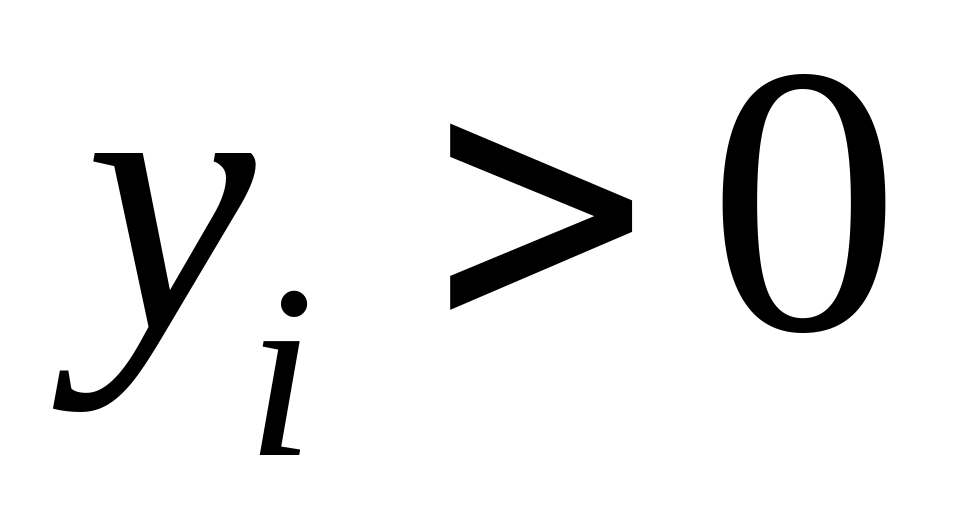 ,
то
;
(38.3)
,
то
;
(38.3)если
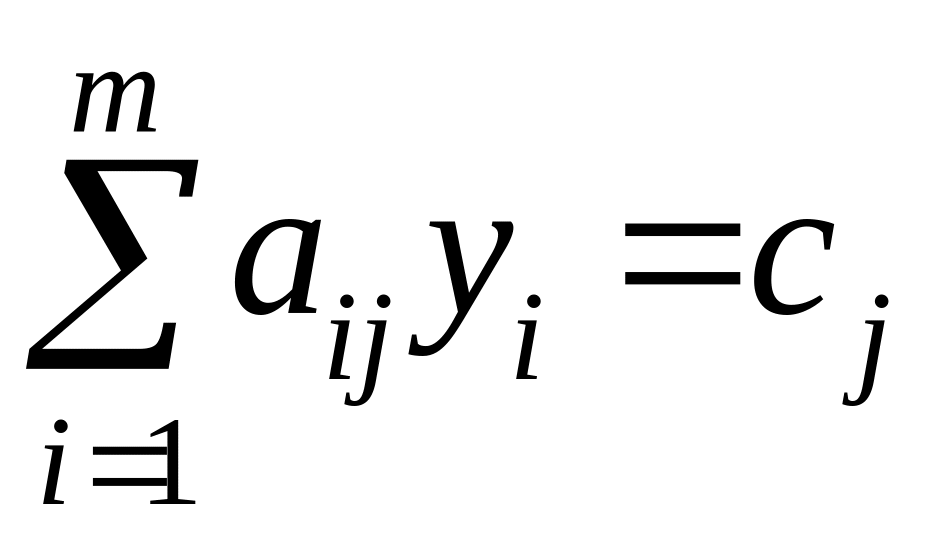 ,
то
,
то
 ;
(38.4)
;
(38.4)если
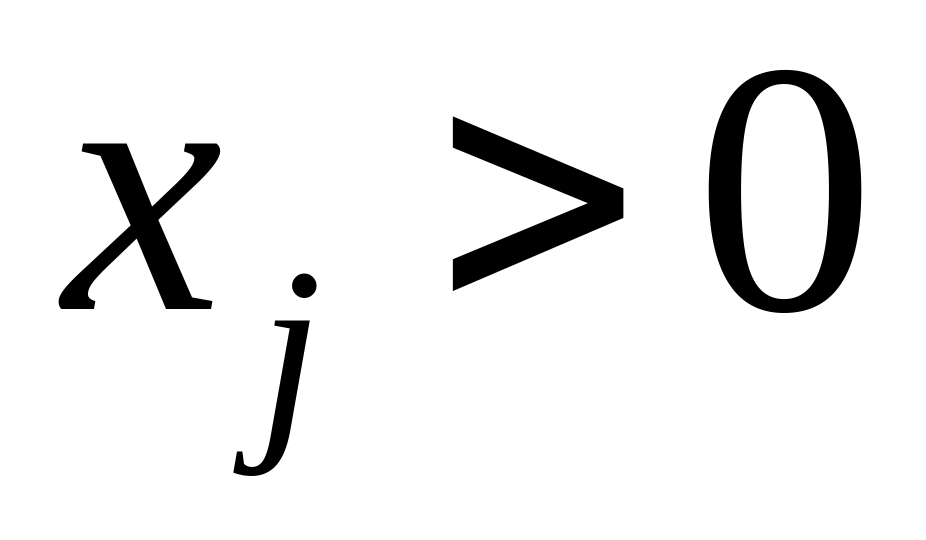 ,
то
.
(38.5)
,
то
.
(38.5)
Пример: используя теоремы двойственности, решить двойственную задачу, если известно решение прямой задачи.
![]()
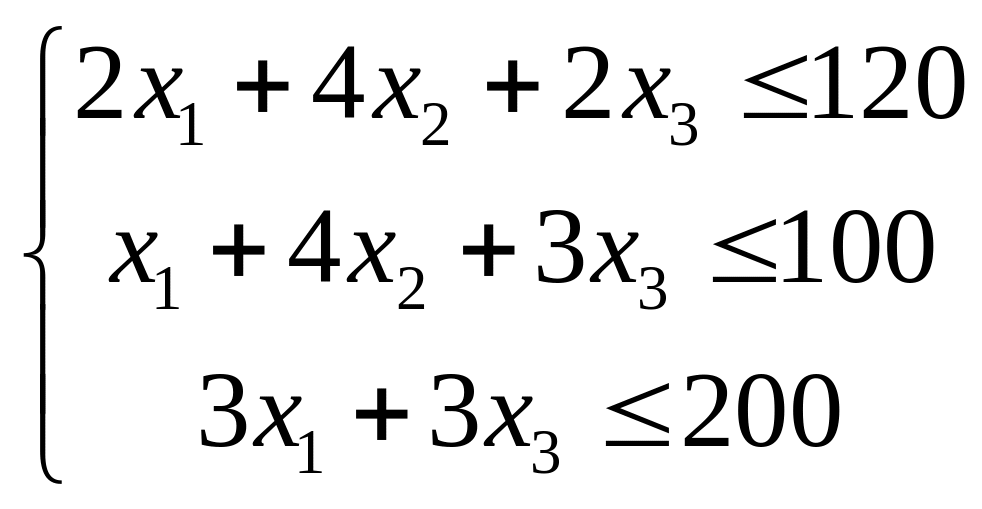 ,
(38.6)
,
(38.6)
,
,![]() .
.
Пусть решение
задачи найдено одним из стандартных
методов:
![]() ,
,
![]() .
.
Построим двойственную задачу:
![]()
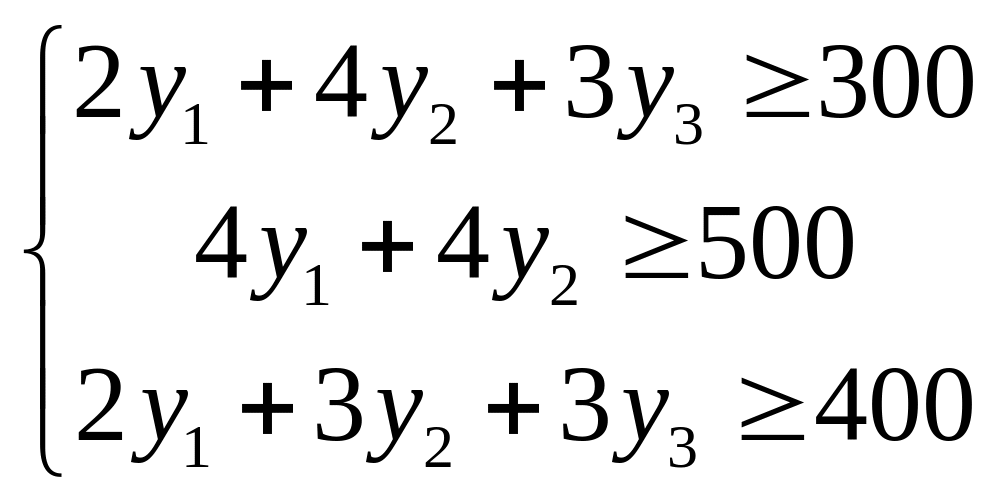 ,
(38.7)
,
(38.7)
,![]() ,
.
,
.
По первой теореме двойственности задача разрешима, причем
![]() .
.
Найдем оптимальный
план задачи
![]() ,
используя вторую теорему двойственности.
Подставим координаты вектора
,
используя вторую теорему двойственности.
Подставим координаты вектора
![]() в ограничения
задачи (38.6).
в ограничения
задачи (38.6).
Получим
![]()
![]()
![]()
Следовательно,
неравенство
![]() должно выполняться как равенство, то
есть
должно выполняться как равенство, то
есть
![]() .
.
Далее, так как
![]() ,
,
![]() ,
то
,
то
![]() ,
,
![]() .
.
Получаем систему линейных уравнений:
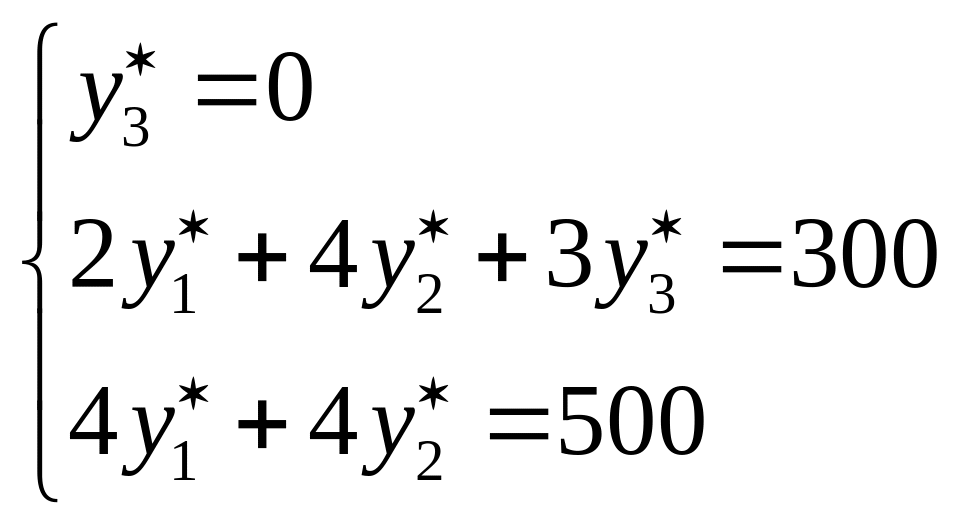 ,
,
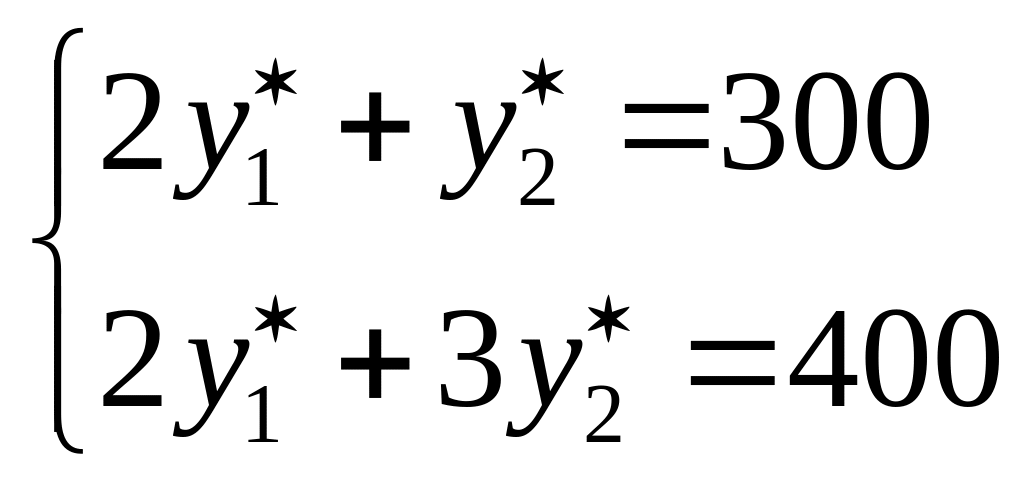 ,
,
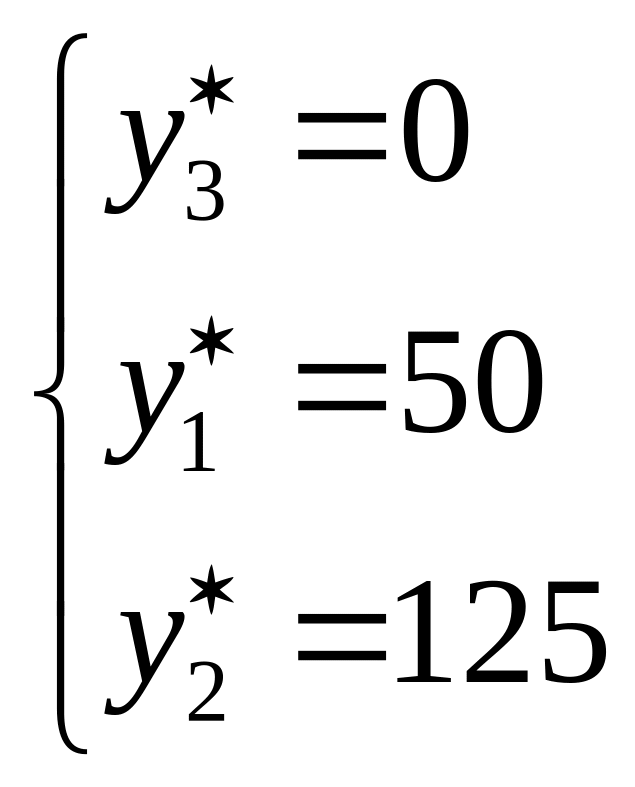
Планы
и
![]() ,
в силу второй теоремы двойственности,
являются оптимальными в задачах (38.6) и
(38.7) соответственно.
,
в силу второй теоремы двойственности,
являются оптимальными в задачах (38.6) и
(38.7) соответственно.
