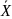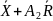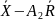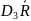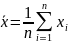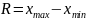3 Графическое представление статистических данных с помощью гистограммы

Гистограммы – это столбиковые диаграммы, показывающие количественную оценку частоты попадания зарегистрированных событий в установленные интервалы. Их используют для представления структуры и характера изменчивости данных, которые трудно заметить при их табличном представлении.

Обычно предметом тщательного изучения служит форма гистограммы. Ее интерпретация позволяет выявить проблемы в процессе.

Гистограммы применяются везде, где требуется проведение анализа точности и стабильности процесса, наблюдение за качеством продукции, отслеживание существенных показателей производства. Гистограмма - один из инструментов статистического контроля качества. Японский союз ученых и инженеров в 1979 г. включил гистограммы в состав семи методов контроля качества.

Порядок построения гистограммы включает в себя 5 этапов:

1. сбор данных, определение минимального и максимального значений, определение размаха гистограммы;

2. диапазон гистограммы делится на интервалы, причем число и ширина интервалов определяется предварительно;

3. распределение данных по интервалам;

4. производится расчет частоты попадания значений в каждый интервал;

5. по полученным данным строится гистограмма, причем высота столбиков соответствует частоте попаданий данным в интервал.

Собранные данные служат источником информации в процессе анализа с использованием различных статистических методов и выработке мер по улучшению качества процессов. [3]

При построении гистограммы на оси абсцисс откладываются величины интервалов, а на оси ординат – частоты. Запишем данные интервального ряда в виде следующей таблицы:

Таблица 6 – Интервальный ряд распределения

Интервал значений	39,3-39,5	39,5-39,7	39,7-39,9	39,9-40,1	40,1-40,3	40,3-40,5	40,5-40,7	40,7-40,9	40,9-41,1	41,1-41,3	41,3-41,5	41,5-41,7
hi	10	17	23	39	16	8	11	6	6	6	4	4

Представим эти значения в виде гистограммы (рисунок 1).

Рисунок 1 – Гистограмма распределения интервального ряда

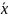
Данная гистограмма не центрирована. Возможности этого процесса, вероятнее всего, не достаточны для выполнения заказа. Гистограмма имеет положительно скошенное распределение. Такая форма встреча­ется, когда нижняя граница регу­лируется либо теоретиче­ски, либо по значению допуска или когда правое значение не­достижимо; статистический ряд в виде гистограммы не согласуется с кривой теоретического нормального распределения

4 ПРОВЕРКА СОГЛАСИЯ ОПЫТНОГО РАСПРЕДЕЛЕНИЯ С ТЕОРЕТИЧЕСКИМ НОРМАЛЬНЫМ

При планировании и проведении выборочного контроля по количественному признаку предполагают, что контролируемый параметр имеет точно или приближенно нормальное распределение с математическим ожиданием  и дисперсией 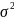. Но на практике данное условие не всегда выполняется, поэтому целесообразно осуществить проверку согласия опытного распределения контролируемого параметра с нормальным законом. Наибольшее практическое применения имеют критерии согласия Пирсона и Колмогорова.

Рассмотрим последовательность проверки гипотезы, с использованием критерия согласия Пирсона:

1. исследуется выборка из генеральной совокупности большого объема n;

2. измеряется значение параметра качества, результаты измерений выполняются в виде интервального ряда;

3. применение критерия Пирсона является обоснованным, при частоте попадания в интервал большей или равной 5 ( );

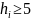4. выдвигается нулевая гипотеза, что распределение генеральной совокупности нормальное, с функцией распределения 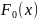и параметрами ₀ и 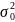: H₀=F(x)=F₀(x). В общем случае параметры ₀ и не известны;

5. проверка гипотезы осуществляется, на основе критерия:

(11)

где 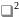- критерий Пирсона;

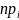- теоретическая частота i-того интервала значений х.

6. Находятся статистические характеристики выборки и ;

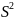7. При расчете теоретических частот распределения учитывают, что p_i – вероятность того, что наблюдаемая случайная величина x генеральной совокупности попадает в i-тый интервал, т.е. x располагается между верхней и нижней границами i-того интервала;

8. производится переход к нормированной случайной величине:

,

(12)

где х_i – верхняя граница i-того интервала,

,

(13)

где F(U) – функция распределения нормированного нормального распределения случайной величины U. При этом верхняя граница i-1-ого интервала равна нижней границе i-ого интервала.

9. все расчеты оформляются в таблице:

И нтервал xi - xi-1	hi	Ui	F(Ui)	pi=F(Ui)-F(Ui-1)	npi	(hi – npi)	(hi–npi)2
1	2	3	4	5	6	7	8	9

² рассчитывается как сумма последнего (9) столбца таблицы.

10. выбирается вероятность ошибки ;

11. решается вопрос о числе степеней свободы m.

m=k-3,

(14)

где k – число интервалов.

12. при вероятности ошибки  критическое значение 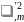определяется из соотношения:

,

(15)

где критическое значение находят по таблице значений для различных m и . Соотношение 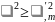означает отклонение от гипотезы H_0.

Т.о. исходя из теоретических выкладок, выполним проверку согласия опытного распределения с теоретическим нормальным. [1]

Исследуется выборка объемом n=150, были измерены значения параметра качества, результаты измерений были представлены в виде интервального ряда:

Таблица 7 – Интервальный ряд распределения выборки объемом n=150

Интервал значений	39,3-39,5	39,5-39,7	39,7-39,9	39,9-40,1	40,1-40,3	40,3-40,5	40,5-40,7	40,7-40,9	40,9-41,1	41,1-41,3	41,3-41,5	41,5-41,7
hi	10	17	23	39	16	8	11	6	6	6	4	4

Расчет средней арифметической и дисперсии интервального ряда приведен в п.2, откуда 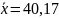, S=0,55.

Таблица 8 – Результаты расчетов критерия согласия Пирсона

И нтервал xi - xi-1	hi	Ui	F(Ui)	pi=F(Ui)-F(Ui-1)	npi	(hi – npi)	(hi–npi)2
39,3-39,5	10	-1,22	1-0,888=0,112	0,112	16,8	6,8	46,24	2,75
39,5-39,7	17	-0,85	1-0,802=0,198	0,086	12,9	4,1	16,81	1,3
39,7-39,9	23	-0,49	0,312	0,114	17,1	5,9	34,81	2,04
39,9-40,1	39	-0,13	0,448	0,136	20,4	18,6	345,96	16,96
40,1-40,3	16	0,24	0,595	0,147	22,05	6,05	36,6	1,66
40,3-40,5	8	0,6	0,725	0,135	19,5	11,5	132,25	6,78
40,5-40,7	11	0,963	0,831	0,106	15,9	4,9	24,01	1,51
40,7-40,9	6	1,33	0,905	0,074	11,1	5,1	26,01	2,34
40,9-41,1	6	1,7	0,955	0,05	7,5	1,5	2,25	0,3
41,1-41,3	6	2,05	0,977	0,02	3,3	2,7	7,29	2,2
41,3-41,5	4	2,42	0,992	0,015	2,25	1,75	3,06	1,36
41,5-41,7	4	2,78	0,977	0,005	0,75	3,25	10,56	14,08
								2 =53,28

По формуле (12) рассчитываем нормированную случайную величину, получаем:

U₁= ;

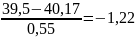U₂= ;

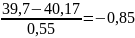U₃= ;

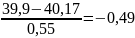U₄= ;

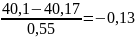U₅= ;

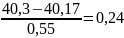U₆= ;

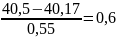U₇= ;

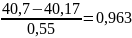U₈= ;

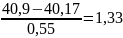U₉= ;

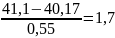U₁₀= ;

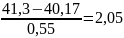U₁₁= ;

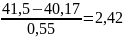U₁₂= .

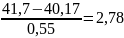Заносим получившиеся данные в таблицу 8. Далее по таблице значений функций нормированного нормального распределения находим F(U_i). Вследствии симметрии нормального распределения F(-U)=1- F(U). Данные сразу заносим в таблицу 8.

Затем производим расчет вероятности попадания случайной величины х генеральной совокупности в i-тый интервал, используя формулу (13):

;

;

;

;

;

;

;

;

;

;

.

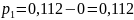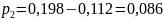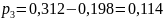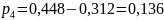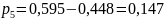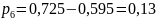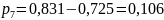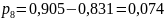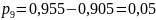
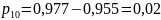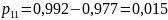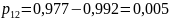Далее необходимо рассчитать теоретические частоты исходя из произведения объема выборки, на вероятность попадания случайной величины в интервал: np_i , учитывая, что объем выборки равен 150 шт.:

np₁=1500,112=16,8;

np₂=1500,086=12,9;

np₃=1500,114=17,1;

np₄=1500,136=20,4;

np₅=1500,147=22,05;

np₆=1500,135=19,5;

np₇=1500,106=15,9;

np₈=1500,074=11,1;

np₉=1500,05=7,5;

np₁₀=1500,02=3,3;

np₁₁=1500,015=2,25;

np₁₂=1500,005=0,75.

После подсчета теоретических частот, следует найти разницу между фактической частотой попадания в интервал и полученным значением теоретических частот:

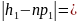|10-16,8|=6,8

17-12,9|=4,1;

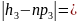|23-17,1|=5,9;

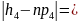|39-20,4|=18,6;

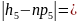16-22,05|=6,05;

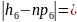|8-19,5|=11,5;

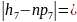|11-15,9|=4,9;

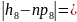|6-11,1|=5,1;

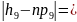|6-7,5|=1,5;

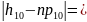|6-3,3|=2,7;

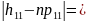|4-2,5|=1,75;

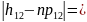7-0,75|=3,25;

Расчет оставшихся данных производим в таблице 8. Получаем критерий Пирсона: ²=53,28.

Т.к. в нашем случае ₀ и не известны, то число степеней свободы m находим используя формулу (14):

m=12-3=9.

Заданная вероятность ошибки =0,05 , тогда исходя из этих данных по таблице значений для различных  и m находим:

.

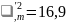Т.о. получаем следующее неравенство:

,

что говорит о том, гипотеза не принимается и опытное распределение генеральной совокупности не является нормальным распределением.

5 ПОСТРОЕНИЕ И АНАЛИЗ КОНТРОЛЬНЫХ КАРТ СРЕДНИХ АРИФМЕТИЧЕСКИХ И РАЗМАХОВ

Основным инструментом статистического управления процессами являются контрольные карты (карты Шухарта) – это графический способ представления и сопоставления информации, основанный на последовательности выборок, отражающих текущее состояние процесса, с границами, установленными на основе изменчивости присущей процессу. Нанесенные на график данные сравниваются с контрольными границами. Точка графика, находящаяся вне области контрольных границ, дает сигнал о возможном изменении процесса из-за действия особой причины. Таким сигналом могут быть другие сочетания расположения точек на графике.

Цель контрольных карт – обнаружить неестественные изменения в данных из повторяющихся процессов и дать критерии для обнаружения отсутствия статистической управляемости. Процесс находится в статистически управляемом состоянии, если изменчивость вызвана только случайными причинами. При определении этого приемлемого уровня изменчивости любое отклонение от него считают результатом особых причин, которые необходимо выявить, исключить или ослабить. [3]

Теория контрольных карт различает два вида изменчивости. Первый вид – изменчивость из-за «случайных» (обычных) причин. Эти причины бесчисленны, разнообразны, присутствуют постоянно. Их нелегко, или невозможно выявить. Каждая из таких причин составляет очень малую долю общей изменчивости, и ни одна из них не значима сама по себе. Тем не менее, сумма всех этих причин существенна и предполагается, что она внутренне присуща процессу. Исключение или уменьшение влияния обычных причин требует управленческих решений и выделения ресурсов на улучшение процесса и системы в целом. Изменчивость процесса, на который действуют только обычные, присущие ему причины во времени стабильна, т.е. он статистически устойчив. Такой процесс предсказуем с точки зрения его возможностей.

Второй вид изменчивости – реальные перемены в процессе. Они могут быть следствием некоторых определенных причин, не присущих процессу внутренне и могут быть устранены, по крайней мере, теоретически. Эти выявляемые причины рассматриваются как «неслучайные» или «особые» причины изменчивости. К ним могут быть отнесены, например, поломка инструмента, недостаточная однородность материала, отказы производственного или контрольного оборудования, недостаточная квалификация персонала, невыполнение процедур, ошибки в выполнении процедур и т.п. Изменчивость процесса, на который действуют особые, не присущие ему причины, во времени нестабильна, т.е. он статистически неустойчив. Такой процесс непредсказуем с точки зрения его возможностей. Он может в любой момент дать продукцию, не соответствующую требованиям потребителей.

Цель контрольных карт – обнаружить неестественные изменения в процессе, т.е. изменчивость второго вида и дать критерии для обнаружения отсутствия статистической управляемости.

Карты для количественных данных отражают состояние процесса через разброс (изменчивость от единицы к единице) и через расположение центра (среднее процесса). Поэтому контрольные карты для количественных данных принято применять и анализировать парами – одна для расположения, другая для разброса. Контрольная карта имеет центральную линию (CL), соответствующую эталонному значению характеристики. При оценке того, находится ли процесс в статистическом управляемом состоянии, эталонным обычно служит среднее арифметическое значение рассматриваемых данных. При управлении процессом эталонным служит долговременное значение характеристики.

Данные карты имеют две статистические определяемые границы относительно центральной линии, которые называют верхней контрольной границей (UCL) и нижней контрольной границей (LCL). [4]

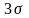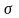
Контрольные границы находятся на расстоянии от центральной линии, где  внутригрупповое стандартное отклонение используемой статистики. Границы указывают, что около 99,7 % значений характеристик подгрупп попадают в эти пределы при условии, что процесс находится в статистически управляемом состоянии. Другими словами, есть риск равный 0,3 % (или в среднем 3 на тысячу случаев), что нанесенная точка окажется вне контрольных границ, когда процесс стабилен. В результате неправильно решают, что процесс вышел из состояния статистической управляемости, и делают попытку выявления несуществующей проблемы. В этом случае говорят об ошибке первого рода.

Контрольные границы иногда называют «границы действий». Попадание точки вне этих границ считается сигналом к действию. Часто на контрольной карте проводят еще границы на расстоянии 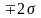. Любое выборочное значение, попадающее за эти границы, служит предостережением о грозящей ситуации выхода процесса из состояния статистической управляемости. Эти границы иногда называют «предупреждающими».

Ошибки второго рода возникают, когда рассматриваемый процесс не управляем, а точки случайно оказываются внутри контрольных границ. В этом случае неверно заключают, что процесс статистически управляем и упускают возможность предупредить рост выхода несоответствующей продукции. Риск ошибки второго рода – функция трех факторов: ширины контрольных границ, степени неуправляемости и объема выборки.

Система карт Шухарта учитывает только ошибки первого рода, равные 0,3 % в пределах границ .

Основным критерием выхода процесса из состояния статистической управляемости является попадание одной из точек на контрольных картах вне контрольных границ. Помимо этого необходимо рассмотреть расположение точек на наличие особых структур также маловероятных, как и выход точки за контрольные границы.

Для оценки необычных структур на -карте, существует набор из 7 дополнительных критериев:

1. Девять точек подряд находятся в зоне С или по одну сторону от центральной линии;

2. Имеются шесть возрастающих или убывающих подряд точек;

3. Четырнадцать попеременно возрастающих и убывающих точек;

4. Две из трех последовательных точек находятся в зоне А;

5. Четыре из пяти последовательных точек находятся в зоне В или вне ее;

6. Пятнадцать последовательных точек находятся в зоне С, выше или ниже центральной линии;

7. Восемь последовательных точек находятся по обеим сторонам центральной линии и ни одной в зоне С.

На контрольной карте наносят вертикальные оси для и R и горизонтальные для номера подгрупп. Построение контрольной карты начинается с нанесения центральной линии (CL) и верхней (UCL) и нижней (LCL) контрольных границ.

Области между центральной линией и контрольными границами разбивают на 3 равные по ширине зоны С, В, А. На подготовленные таким образом карты наносятся для каждой подгруппы посчитанные значения средних -на карту средних арифметических и посчитанные значения R на карту размахов. При оценке результатов анализа полученных карт считают, что процесс находится в стадии статистической управляемости, если отсутствуют точки, выходящие за пределы контрольных границ и необычные структуры точек. [4]

Формулы для нахождения центральной и контрольной границ представлены в таблице 9.

Таблица 9 – Формулы для центральной и контрольных границ контрольных карт и R

Х арактеристика	Стандартные значения не заданы
	CL	UCL	LCL
X
R

Коэффициенты для вычисления линий контрольных карт, для значений подгруппы равной 5, представлены в таблице 10.

Таблица 10 – Коэффициенты для вычисления линий контрольных карт

Ч исло наблюдений	А2	D3	D4
5	0,577	2,114	0,000

Для построения контрольных карт является необходимым произвести расчет средних арифметических значений и размахов каждой из подгрупп (таблица 11). Среднее значение подгруппы определяется по следующей формуле:

(17)

где n – объем подгруппы (выборки).

Размах подгруппы определяют как разность наибольшего и наименьшего значений в подгруппе:

(18)

Таблица 11 – Расчет средних арифметических и размахов

№ выборки	Х1	Х2	Х3	Х4	Х5		R
1	40,5	40,1	39,7	39,8	39,7	39.96	0,8
2	40,3	40,5	40,7	41,4	40,9	40.76	0,6
3	40,0	39,7	39,3	39,8	39,9	39.74	0,7
4	39,6	41,1	40,5	41,2	40,4	40.56	1,6
5	40,0	39,9	40,0	40,5	39,9	40.06	0,6
6	39,3	40,5	39,4	40,0	40,5	39.94	1,2
7	39,3	41,0	39,7	40,8	40,2	40.2	1,7
8	40,0	39,9	40,3	40,0	40,0	40.04	0,4
9	41,7	40,1	39,8	39,8	39,5	40.18	2,2
10	40,0	40,1	39,6	39,7	39,9	39.86	0,5
11	40,0	39,9	40,0	39,7	39,5	39.82	0,5
12	39,7	39,9	40,0	41,3	40,0	40.18	1,6
13	39,5	39,3	40,2	41,3	40,1	40.08	2
14	40,7	40,1	40,5	41,0	39,7	40.4	1,3
15	40,0	40,1	41,6	40,3	41,6	40.72	1,6
16	40,7	39,8	40,0	41,2	41,5	40.64	1,7
17	40,0	40,1	39,4	39,5	40,0	39.8	0,7

П родолжение таблицы 11

18	39,8	39,6	39,5	39,4	40,8	39.82	1,4
19	41,1	40,0	39,6	39,8	39,9	40.08	1,5
20	40,5	40,0	39,7	40,2	40,0	40.08	0,8
21	40,0	39,8	40,0	40,4	40,2	40.08	0,4
22	40,0	41,3	39,9	41,1	39,8	40.42	1,5
23	40,4	40,4	39,6	40,1	39,7	40.04	0,8
24	39,9	39,5	39,8	40,2	39,5	39.78	0,7
25	39,7	39,6	40,6	39,7	40,6	40.04	1
26	39,5	39,9	40,0	40,7	39,3	39,88	1,4
27	40,0	41,1	39,6	40,2	41,4	40,46	1,8
28	39,9	39,5	40,9	40,0	40,5	40,16	1
29	39,4	39,9	39,7	40,0	39,6	39,72	0,6
30	40,1	40,0	39,9	41,0	39,4	40,08	1,6
						∑=1203,58	∑=34,2

Далее производим расчет центральной линии, верхней и нижней контрольных границ для R-карт, используя формулы из таблицы 9:

CL = 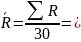34,2/30=1,14;

ULC = ;

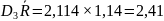LCL =

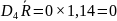
Также следует произвести расчет контрольных границ и центральной линии для карты средних ( ):

CL = = ;

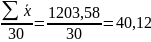UCL =

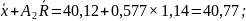
LCL =

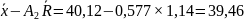
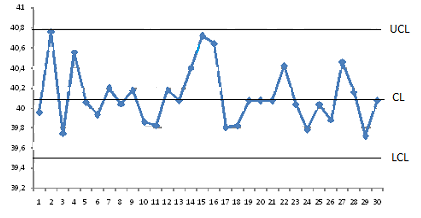
По полученным данным строим контрольные карты средних ( ) и размахов (R), (рисунок 2 и 3). Анализируя контрольную карту размахов можно прийти к выводу, что процесс является статистически управляемым, так как отсутствуют точки, выходящие за пределы контрольных границ, необычные структуры точек, т.е. данный процесс является приемлемым, и не требуется настройка процесса по разбросу. Анализ контрольной карты средних ( ) позволяет также судить о том, что процесс статистически управляем, качество продукции предсказуемо, и процесс пригоден для удовлетворения требований, установленных в нормативных документах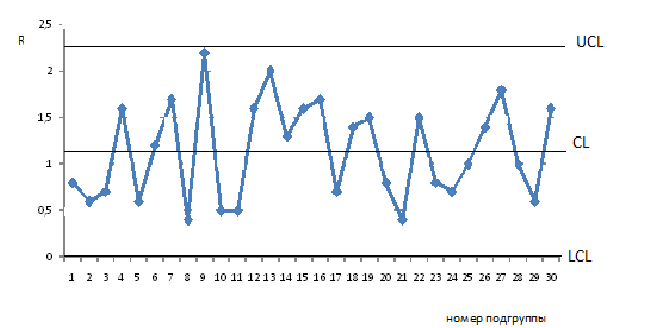

Рисунок 2 – Контрольная карта размахов (R)

.

	Рисунок 3 – Контрольная карта средних арифметических ( )
	.
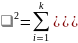
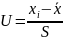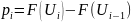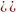
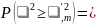