2.5. Обчислення довжин кривих

1. Знайдемо довжину дуги кривої Скористаємося відомою формулою

(2.13)

тоді отже, довжина дуги .

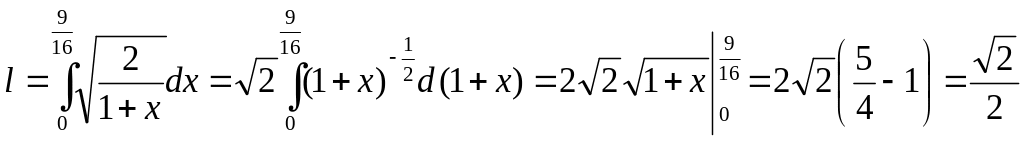2 . Знайти довжину дуги астроїди . (мал. 2.7) Приймаючи до уваги, що крива задана в параметричній формі, використаємо відому формулу для знаходження довжини дуги в цьому випадку: де і – відповідно значення параметра на початку і в кінці дуги. Враховуючи симетричність кривої відносно осей координат, одержуємо:

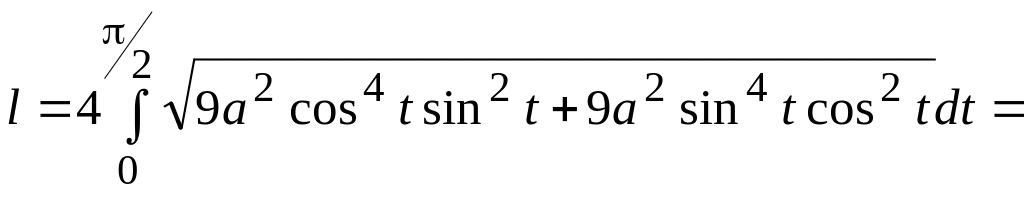
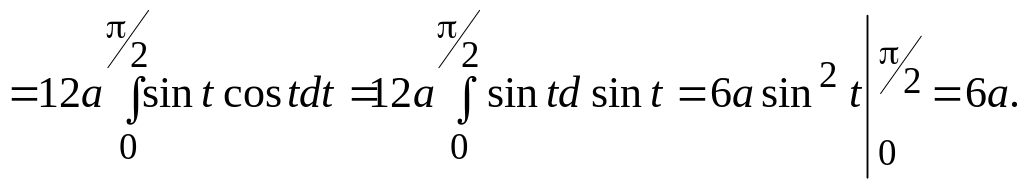(2.14)

3. Знайти довжину замкненої кривої Для знаходження довжини дуги, заданої в полярних координатах, використаємо відому формулу:

(2.15)

де , причому – неперервно диференційована на функція. Оскільки то Звідси При зміні від 0 до довжина радіус-вектора зростає від 0 до , а кінець радіус-вектора описує дугу ОАМВ (мал. 2.8). Потім при зміні від до величина зменшується від до 0, при цьому описується дуга ВСАО, симетрична дузі ОАМВ відносно прямої Тепер обчислимо довжину кривої

4. Знайти довжину дуги просторової кривої Довжина просторової кривої, заданої параметричними рівняннями , де – неперервно диференційовані на функції, дорівнює: За параметр виберемо змінну , тоді причому Тоді після спрощень .

2.6. Обчислення об’ємів тіл

Нехай функція неперервна і невід’ємна на сегменті . Об’єм тіла утвореного обертанням навколо осі криволінійної трапеції (мал. 2.1), обмеженої графіком функції , відрізками прямих та і відрізком осі , дорівнює

(2.17)

Якщо функція задана параметричними рівняннями , де функція має неперервну невід’ємну похідну на і а функція неперервна на , то об’єм тіла, утвореного обертанням тієї ж криволінійної трапеції навколо осі , дорівнює

(2.18)

Нехай тіло розміщене в просторі між площинами кожен переріз тіла площиною, перпендикулярною до осі , має площу , де – інтегровна на функція. Якщо це тіло має об’єм, то він дорівнює:

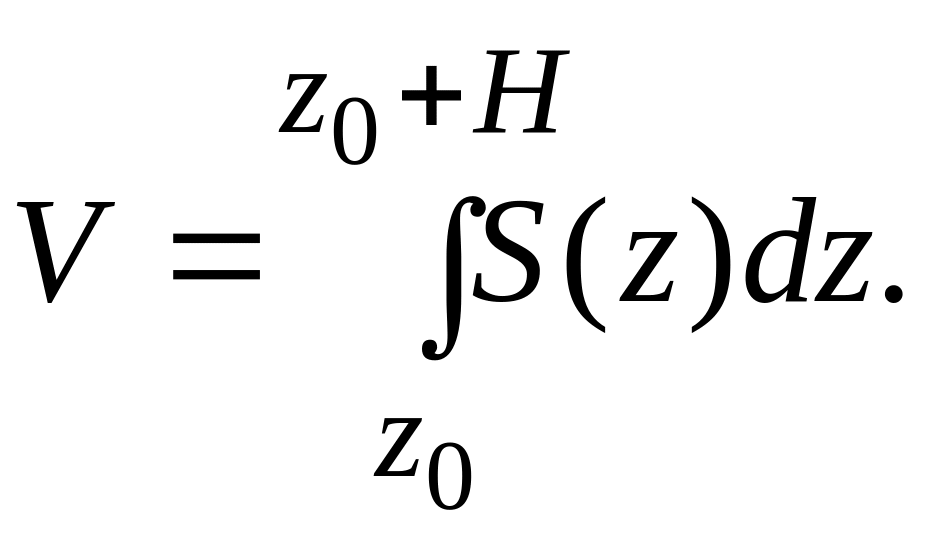(2.19)

Аналогічні формули мають місце, якщо замість осі взяти вісь або .

Знайти об’єм тіла, утвореного при обертанні навколо осі фігури, обмеженої данними кривими.

1 . В утворенній фігурі обертання приймають участь три прямі та рівностороння гіпербола (мал. 2.9). По формулі (2.17)

(куб.од.) На мал. 2.9 заштрихована криволінійна трапеція, яку обертають навколо осі .

2.

Знайдемо точки перетину двох парабол. Розв’яжемо систему Маємо тоді звідки Об’єм тіла обертання знайдемо як різницю об’ємів двох тіл обертання, утворених відповідно обертанням параболи і другої параболи (мал. 2.10): 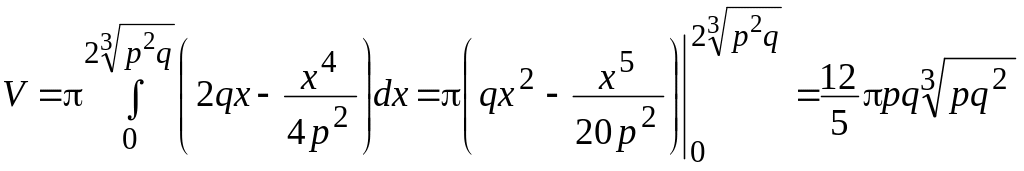(куб.од.)

3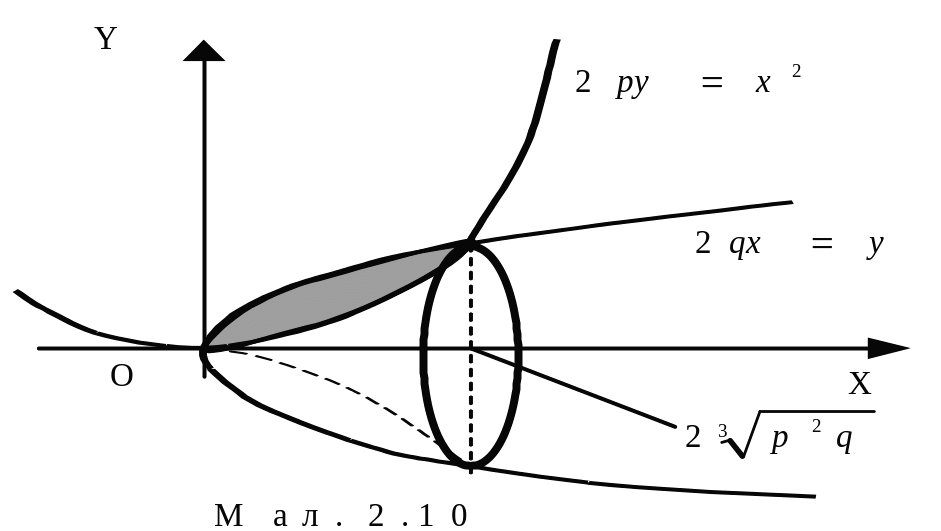 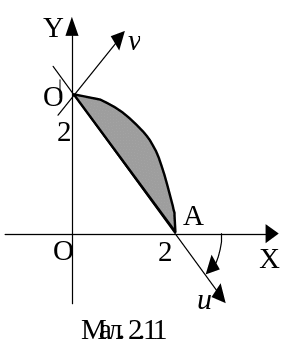. Знайти об’єм тіла, утвореного при обертанні фігури, обмеженої параболою і прямою , навколо прямої . Зробивши поворот і зсув (перенос), перейдемо в систему координат вісь якої розміщена на осі обертання прямої (мал.2.11). Кут повороту, як це витікає з рівняння прямої, дорівнює Формули переходу мають вигляд: В цій системі координат парабола буде задана параметричними рівняннями де Дуга параболи відповідає відрізку Об’єм тіла обертання

Нехай функція неперервна на , . Можна довести, що об’єм тіла, утвореного при обертанні навколо полярного променя дорівнює:

(2.20)

4. Знайти об’єм тіла, утвореного при обертанні навколо полярного променя фігури, заданої в полярних координатах нерівностями: , По формулі (2.20) Покладемо тоді а змінна змінюється від 1 до . Маємо

5. Знайти об’єм трьохосьового еліпсоїда

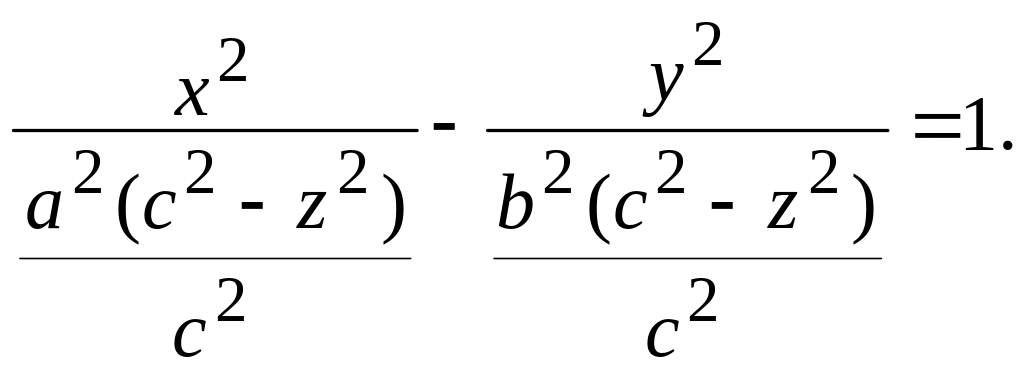Для розв’язування задачі скористаємося формулою (2.19) і тим відомим фактом, що площа, обмежена еліпсом з півосями і , дорівнює Перетин еліпсоїда площиною представляє собою еліпс, причому його площа – функція . Зрозуміло, що Цей перетин має рівняння або Тоді По формулі (2.19) об’єм еліпсоїда

Зокрема, для кулі маємо та