84. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Обобщение на случай уравнения n-ного порядка.
(1)
Для
нахождения
достаточно найти два частных линейно
независимых решений
и
Эйлер
предложил искать частные решения в виде
,
(2)
(3)
– характеристическое уравнение (1)
1 случай
корни характеристического уравнения действительны и различны
В
этом случае частными решениями будут
функции:
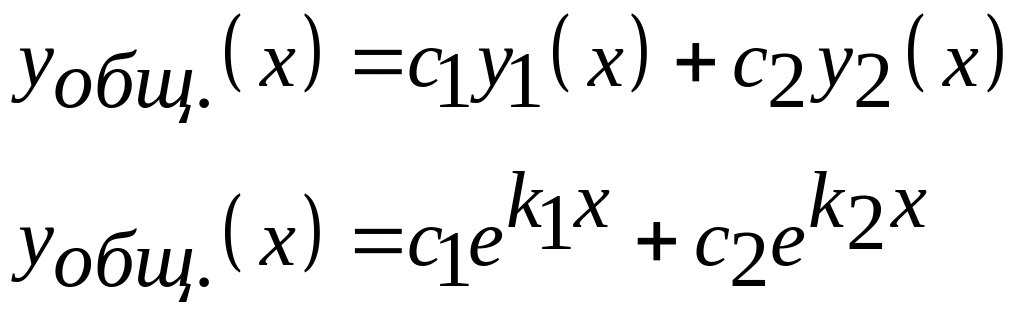
2 случай
корни характеристического уравнения комплексные
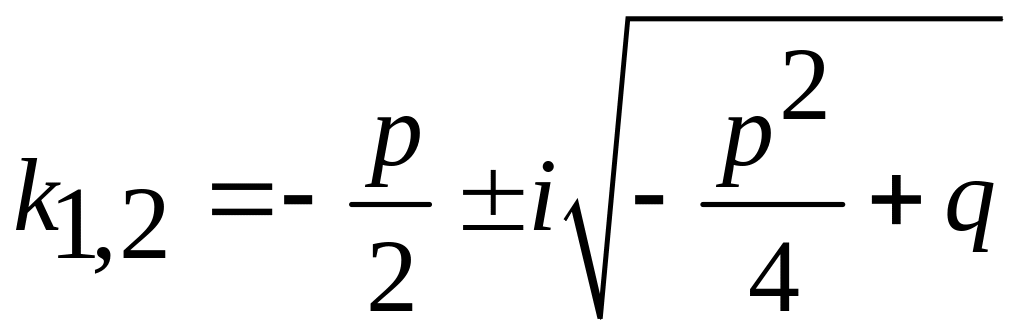
Частное
решение:
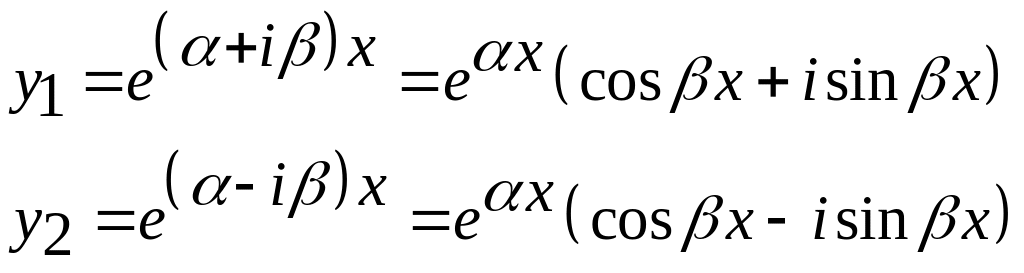
По теореме, действительная и мнимая части будут решениями, т.е. решениями будут действительные функции
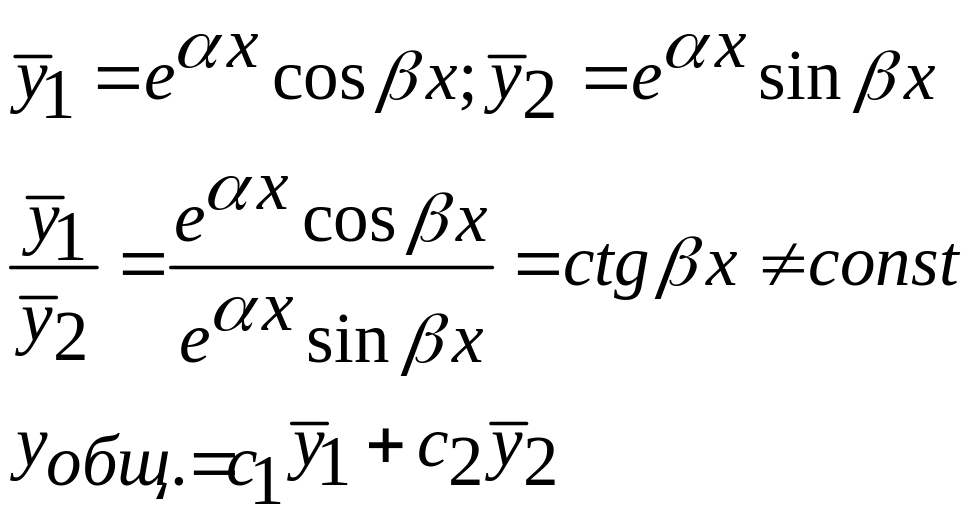
3 случай
корни характеристического уравнения действительны и равны
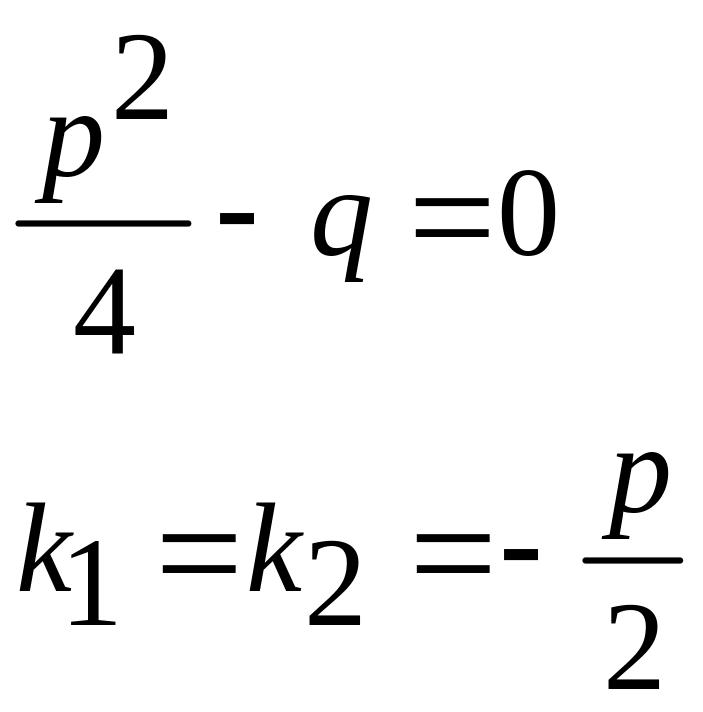
Одно
частное решение получается
.
Второе частное решение независимое с
первым будем искать в виде:
где
неизвестная
функция, подлежащая определению
85. Лінійні неоднорідні диференціальні рівняння 2го порядку зі сталими коефіцієнтами. Метод варіації довільних сталих.
Уравнение вида
,
где , - функция от и , называется неоднородным диф-ным ур-нием 2го порядка с постоянными коэффициентами.
Метод вариации произвольных постоянных используется для нахождения частного решения лин. неоднороднного диф. ур. 2-го порядка с постоянными коэффициентами, при любом виде правой части . Суть решения:
Отыскивается общее решение соответствующего однородного уравнения ( т.е. ):
.
Частное решение неоднородного диф. ур. ищется в виде:
(т.е. заменяются на функции времени ).
Функции ( ) определяются из системы:
.
Общее решение неоднородного ур. Определяется в виде суммы: общего решения однородного ур. и частного решения неоднородного ур. :
.
Пример:
Пусть
Определим неизвестные ф-ции и из системы:
Решаем систему по методу Крамера:
Общее решение
.
86. Решение систем дифференциальных уравнений методом исключений.
Одним из основных методов интегрирования системы дифференциальных уравнений является сведение к уравнению более высокого порядка, состоящего в следующем: из уравнений системы (1)
и из уравнений, получающихся дифференцированием уравнения, входящего в систему, исключают все неизвестные функции, кроме одной, для определения которой получают одно дифференциальное уравнение более высокого порядка. Интегрируя, находят одну из неизвестных функций, а остальные функции определяют из исходных уравнений и уравнений, получившихся в результате их дифференцирования.
Дифференцируя по х первое из уравнений системы (1):
Заменяя производные , на , из системы (1) получим:
Дифференцируя полученное уравнение и поступая аналогично предыдущего, получим:
Продолжая указанную процедуру, получим последнее уравнение:
Итак, получим систему
(2)
Из первых (n-1) уравнений определим , выразив их через и производные , , ,…,
(3)
Подставляя выражения (3) в последнее из уравнений системы (2), получим уравнение n-го порядка для определения .
Решая это уравнение, определим
(4)
Дифференцируя (4) (n-1) раз найдём производные , ,…, как функции от .
Подставляя их в выражение (3), получим
(5)
Тогда выражения (4) и (5) дают решение системы (1). Если дана задача Коши, то из уравнений (4) и (5) определяют значения произвольных констант , .
Замечание 1
указанный процесс исключения всех функций, кроме одной предполагает, что определитель
Только в этом случае, система (2) будет разрешима относительно функций
Замечание 2
Если применить выше указанный метод к линейной однородной системе , то уравнение n-го порядка будет линейным однородным. При чём если все коэффициенты , то и уравнение будет линейным однородным уравнением с постоянными коэффициентами. Аналогичное замечание справедливо и для линейной неоднородной системы, для которой уравнение будет линейным неоднородным уравнением n-го порядка.