Глава 3. Сложное сопротивление прямого бруса

3.1. Общие понятия

В предыдущих главах рассматривались простые случаи нагружения прямого бруса – осевое растяжение (сжатие), плоский поперечный изгиб, кручение.

Возможны более сложные воздействия, при которых в поперечном сечении возникают до шести компонентов внутренних сил. Такое нагружение называется сложным сопротивлением. Удобно рассматривать сложное сопротивление как сочетание простых видов нагружения – растяжения, изгиба и кручения, что возможно для жёстких стержней, к которым применим принцип суперпозиции.

Далее рассмотрим наиболее часто встречающиеся случаи сложного сопротивления.

3.2. Косой изгиб

Это такой случай изгиба бруса, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных осей инерции поперечного сечения.

Рассмотрим балку, заделанную одним концом, на которую действует сила Р, приложенная в центре тяжести концевого сечения под углом φ к оси 0у (рис.3.1,а).

Разложим силу Р на две составляющие по осям координат:

(3.1)

а б

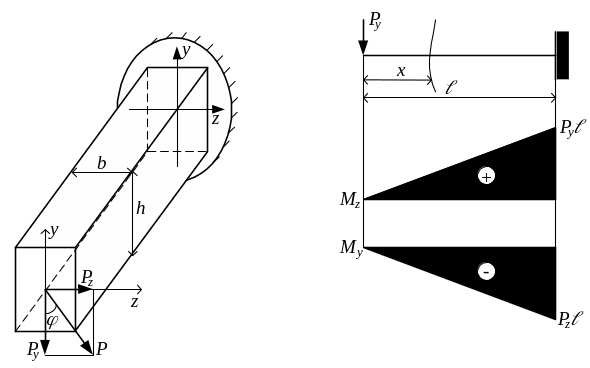
Рис.3.1

В каждом сечении стержня одновременно действуют два изгибающих момента, которые создают изгиб в двух главных плоскостях:

(3.2)

Знак изгибающего момента устанавливается по знаку деформации в первом квадранте. От момента М_z (силы Р_у) верхняя часть бруса удлиняется, нижняя - укорачивается. От момента М_у (силы Р_z) левая часть бруса удлиняется, правая - укорачивается.

Для определения напряжения в произвольной точке, лежащей в первом квадранте, в соответствии с принципом независимости действия сил воспользуемся полученной ранее формулой для нормального напряжения при плоском изгибе (формула (5.18) в первой части курса)

. (3.3)

Знаки напряжений совпадают со знаками изгибающих моментов. Подставляя в формулу (3.3) координаты любой точки с учётом их знаков, получим значение напряжения в этой точке. Для угловых точек модули координат у и z приобретают максимальные значения, поэтому формулу (3.3) можно представить в виде

, (3.4)

где W_z и W_z – моменты сопротивления сечения, i – номер угловой точки.

Знаки устанавливаются по виду деформации от соответствующего изгибающего момента (удлинение – «+», укорочение – «–»). Напомним формулы для определения геометрических характеристик прямоугольника:

, , , .

На рис.3.2,а показано поперечное сечение рассматриваемого бруса, в углах расставлены знаки деформаций в соответствии с физическим смыслом задачи. Подсчитаны напряжения в угловых точках

(3.5)

а б

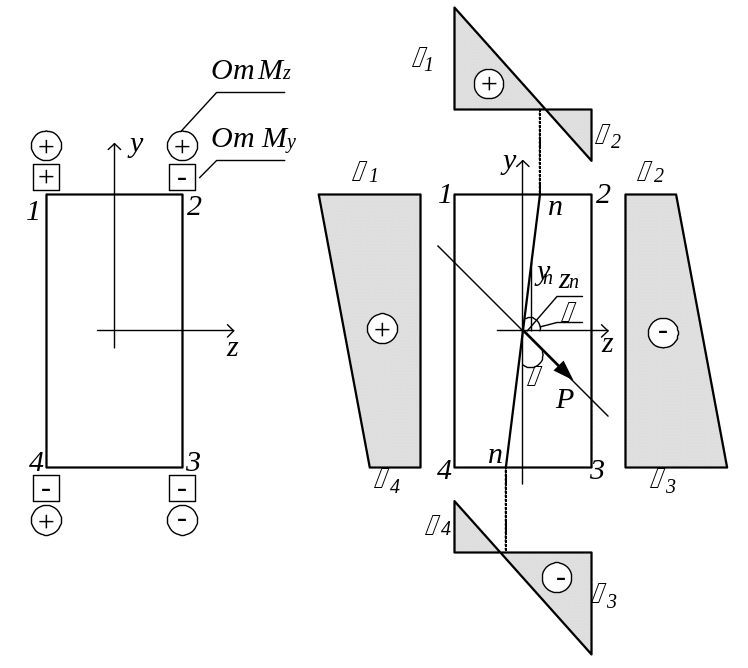
Рис.3.2

По значениям напряжений в угловых точках построили эпюры напряжений по граням сечения (рис.3.2,б). При этом считаем, что . Снеся на грани сечения нулевые точки эпюр напряжений, провели нейтральную или нулевую линию nn – геометрическое место точек с нулевыми напряжениями. Наибольшее и наименьшее напряжения имеют место в точках, наиболее удалённых от нейтральной линии – в точках 1 и 3.

Таким образом, условие прочности при косом изгибе профиля с углами (прямоугольника, двутавра, швеллера) имеет вид

. (3.6)

Положение нейтральной линии можно определить не только графически (рис.3.2,б), но и аналитически. Для этого надо приравнять нулю напряжения в точках, принадлежащих этой линии. Пусть текущие координаты нулевой линии будут z_n и y_n, тогда, применяя формулу (3.3), получим

. (3.7)

Уравнение нейтральной линии (3.7) – это уравнение прямой, проходящей через начало координат. Находим из него

,

. (3.8)

Получили, что нейтральная линия проходит через первую четверть, β – угол между осью z и нейтральной линией.

Если сечение не имеет углов, то для проверки прочности необходимо сначала найти положение нейтральной линии, затем координаты наиболее удалённой от неё точки, затем определить напряжение в этой точке по формуле (3.3) и сравнить его с допускаемым. Необходимо помнить, что знаки в формуле (3.3) ставятся в каждом конкретном случае свои – по знаку деформации в первой четверти.

Найдём перемещение (прогиб) свободного конца бруса. Сначала находим прогибы по направлению главных осей:

, . (3.9)

Суммарный прогиб можно найти как геометрическую сумму

. (3.10)

Найдём теперь направление перемещения υ. Для этого определим значение угла наклона этого перемещения к вертикали:

,

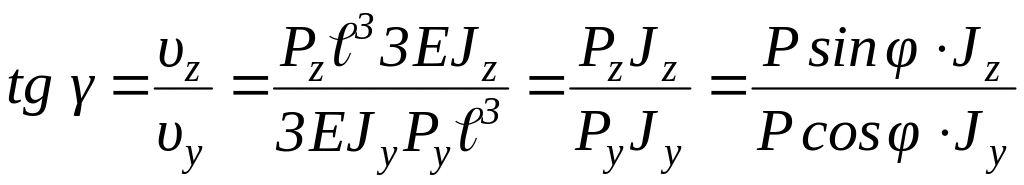. (3.11)

Формула (3.11) идентична формуле (3.8). Это позволяет сделать заключение, что γ = β. Следовательно, направление прогиба перпендикулярно нейтральной линии (рис.3.3,а). В то же время направление прогиба не совпадает с направлением действующей силы, поэтому изгиб называют косым. Нулевая линия не перпендикулярна силовой линии.

а б

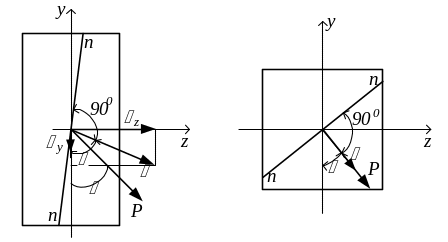
Рис.3.3

В тех сечениях, у которых моменты инерции относительно главных центральных осей равны друг другу (J_z = J_y), нулевая и силовая линии пересекаются под углом 90⁰, а направление прогиба совпадает с силовой линией (рис.3.3,б). К таким сечениям относятся круг, квадрат и другие симметричные профили. В балках с таким сечением косой изгиб невозможен.