Розділ 3. Метод гілок і меж

Метод, відомий як метод гілок і меж, схожий на методи с відходами назад тим, що він досліджує деревоподібну модель простору рішень і застосується для широкого кола дискретних комбінаторних задач. Алгоритми с відходами націлені на те, щоб знайти одну чи всі конфігурації, що модулюються N-векторами, які задовольняють визначеним властивостям. Алгоритми гілок та меж орієнтовані в більшому ступені на оптимізацію. У задачі.що розв'язується, визначена числова функція вартості для кожної з вершин, що з'являються в дереві пошуку. Мета — знайти конфігурацію, на який функція вартості досягає максимального чи мінімального значення.

Алгоритм гілок та меж добре працює в задачі комівояжера. За допомогою алгоритмів гілок та меж можна вирішити велике коло різноманітних серйозних практичних задач , ці алгоритми рідко виявляються простими.

Задача називається симетричної, якщо сij=сji для всіх і і j, тобто якщо вартість проїзду між кожними двома містами не залежить від напрямку.

Алгоритми гілок та меж для задачі комівояжера можуть бути сформульовані різними способами. Автори алгоритму, що викладається -Литл, Мерти, Суини і Карел. Це свого роду класика.

По-перше, розглянемо розгалуження. На Рис. 3.1, а показана матриця вартості для асиметричної (несиметричної) задачі комівояжера с п'ятьма містами, представленої на Рис. 3.1, б. Зверніть увагу на те, що ми користаємося спрямованою мережею, щоб вказати вартості, тому що вартість проїзду з міста і прямо в місто j не обов'язково така ж, як вартість проїзду з міста / у місто і. Корінь нашого пошукового дерева буде відповідати множині «усіх можливих турів», ця вершина представляє множину усіх 4! Можливих турів у нашій задачі с п'ятьма містами. У загальному випадку для будь-якої асиметричної задачі с N містами корінь буде представляти повна множина R усіх (N-1)! можливих турів. Гілки, що виходять з кореня, визначаються вибором одного ребра, скажемо (i,j). Наша мета полягає в тому, щоб розділити множини усіх турів на дві множини: одну, яка, дуже імовірно, містить оптимальний тур, і іншу, котра, імовірно, не містить. Для цього вибираємо ребро (і,1); воно, як ми сподіваємося, входить в оптимальний тур, і розділяємо R на дві множини {і, j} і {і, j}. У множині

{ і, j} входять тури з R, що містять ребро (і, j), а в { і, j} — не утримуючі (і, j).

	1	2	3	4	5
1		25	40	31	27
2	5		17	30	25
3	19	15		6	1
4	9	50	24		6
5	22	8	7	10

Рис. 3.1. Задача комівояжера (а) матриця вартості

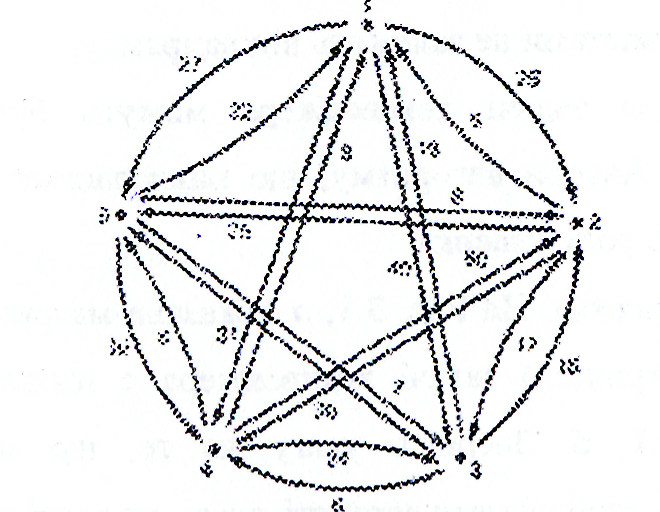
Рис. 3.1. Задача комівояжера (б) мережа з п'яти міст

Припустимо, у нашому прикладі ми робимо розгалуження на ребрі (і, j)=(3,5), що має найменшу вартість у всій матриці. Корінь і перший рівень дерева простору рішень будуть тоді такими, як показано на Рис. 3.2.

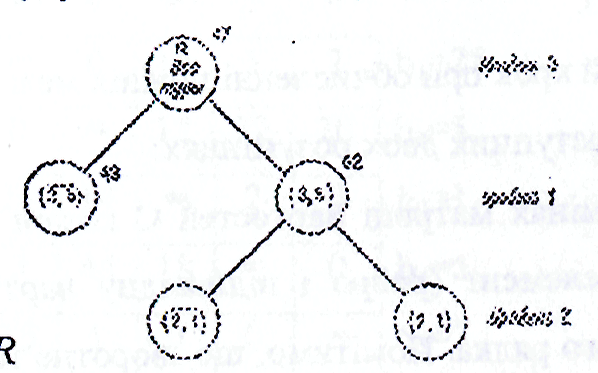
Помітимо, що кожен тур з R

Рис. 3.2. Побудова дерева пошуку по методу гілок та меж.

м іститься тільки в одній множині рівня 1. Якби ми якось могли зробити висновок, що множина {3,5} не містить оптимального туру, то нам потрібно було б досліджувати тільки множину (3, 5}.

Потім розділяємо множину {3, 5} у такий же спосіб, як і множину R. Наступне дешеве ребро в матриці — це ребро (2, 1) з вартістю с₂і=5. Тому можна розділити множину {3, 5} на тури, що включають ребро (2, 1), і тури, що не включають цього ребра; це показано на рівні 2 на рис. 3.2. Шлях від кореня до будь-якої вершини дерева виділяє визначені ребра, що чи повинні не повинні бути включені в множину, представлену вершиною дерева. Наприклад, ліва вершина рівня 2 на рис. 3.2 представляє множина усіх турів, що містять ребро (3, 5) і не утримуючих ребер

(2, 1). Узагалі, якщо X — вершина дерева, а (і, j) — ребро розгалуження, то позначимо вершини, що безпосередньо випливають за X, через Y і Y. Множина У позначає підмножину турів з X с ребром (і, j), а множина Y — підмножину X без (і, j).

С кожною вершиною дерева ми зв'язуємо нижню межу вартості будь-якого туру з множиною, представленого вершиною. Обчислення цих нижніх меж — основний фактор, що дає економію зусиль у будь-якому алгоритмі типу гілок та меж. Тому особлива увага варто приділити одержанню як можна більш точних меж. Причина цього наступна. Припустимо, що ми побудували конкретний повний тур з вартістю т. Якщо нижня межа, зв'язана с множиною турів, представлених вершиною п, дорівнює М>т, то до кінця процесу пошуку оптимального туру не потрібно розглядати вершину v_k і всі наступні за нею.

Основний крок при обчисленні нижніх меж відоме як приведення. Воно асновано на наступних двох розуміннях:

1. У термінах матриці вартостей С кожен повний тур містигь тільки один елемент (ребро і відповідну вартість) з кожного стовпця і кожного рядка. Помітимо, що зворотне твердження не завжди вірне. Множина, що містить один і тільки один елемент із кожного рядка і з кожного стовпця С, не обов'язково представляє тур.

2. Якщо відняти константу h з кожного елемента якогось чи рядка стовпця матриці вартостей С, то вартість будь-якого туру при новій матриці С рівно на h менше вартості того ж туру при матриці С. Оскільки будь-який тур повинний містити ребро з даного рядка чи даного стовпця, вартість усіх турів зменшується на h. Це віднімання називається приведенням рядка (чи стовпця).

Нехай t — оптимальний тур при матриці вартості С. Тоді вартістю туру t буде

Якщо С` виходить з С приведенням рядка (чи стовпця), то t повинний залишитися оптимальним туром при С` і

z(t)=h+z'(t),

де z'(t) — вартість туру t при С`

3

1

2

4

5

	0	15	3	2
0		12	22	20
18	14		2	0
3	44	18		0
15	1	0	0

h

1

2

i=25

h

3

₂=5

h

4

5

₃=l

h4=6

h₅=7

h6 h7 h8 h9 h10

=0 =0 =0 =3 =0

h=25+5+ 1+6+7+3=47

Рис. 3.3. Приведення матриці вартості, показаної на Рис. 3.1, а.

Під приведенням усієї матриці вартості С розуміється наступне. Послідовно проходимо рядка С і віднімаємо значення найменшого елемента hi кожного рядка з кожного елемента цього рядка. Потім того ж саме робимо для кожного стовпця. Якщо для деякого чи стовпця рядка hj=0, то розглянутий чи стовпець рядок уже приведеш, і тоді переходимо до наступного рядка чи стовпчика. Покладемо

h =

Отриману в результаті матрицю вартості назвемо приведеної з С. На Рис. 3.3 показане приведення матриці вартості, зображеної на Рис. 3.1, а. Значення hi дані наприкінці кожного рядка і стовпця (рядка і стовпчики послідовно перенумеровані).

Загальне приведення складає Н=47 одиниць. Отже, нижня межа вартості будь-якого туру з R також дорівнює 47,

z(t) = h+z`(t)>h=47

тому що z' (t)>0 для будь-якого туру t при приведеній матриці С`. Ця межа зазначена біля кореня дерева на Рис. 3.2.

Розглянемо нижні границі для вершин рівня 1, тобто для множин {3, 5} і {3, 5}. Будемо працювати с приведеною матрицею, зображеної на Рис 3.3., маючи на увазі, що значення 47 повинне бути додане до вартості оптимального туру t при С` для того, щоб одержати дійсну вартість t при С.

По визначенню ребро (3, 5) міститься в кожнім турі множини {3, 5}. Цей факт перешкоджає вибору ребра (5, 3), тому що ребра (3, 5) і (5, 3) утворять цикл, а це не допускається ні для якого туру.

Ребро (5, 3) виключаємо з розгляду, поклавши с₅₃= . Рядок 3 і стовпець 5 також можна виключити з подальшого розгляду стосовно множини {3,5}, тому що вже є ребро з 3 у 5. Частина приведеної матриці вартості, показаної на Рис. 3.3, що буде хоч скільки-небудь корисна для подальшого пошуку на множині турів {3, 5}, показана на Рис3.4, а. Вона може бути приведена до матриці вартості, показаної на Рис. 3.4 б з h= 15. Тепер нижня межа для будь-якого туру з множини {3, 5} дорівнює 47+15=62; вона зазначена біля вершини {3, 5} на Рис. 3.2.

Нижня межа для множини {3, 5} виходить трохи іншим способом. Ребро (3, 5) не може знаходитися в цій множині, при цьому припустимо с₃5= в матриці, зображеної на Рис. 3.3. У будь-який тур з {3, 5} буде входиш якесь ребро з міста 3 і якесь ребро до міста 5. Найдешевше ребро з міста 3, крім старого значення (3, 5), має вартість 2, а найдешевше ребро до міста 5 м вартість 0. Отже, нижня межа будь-якого туру в множині {3,5} дорівнює 47+2+0=49; це зазначено біля вершини {3, 5} на Рис. 3.2.

1

0

1 2 3 4 1 2 3 4

	0	15	3
0		12	2
3	44	18
15	1		0

	0	3	3 0
0		0	2 3 2
0	41	3	0
15	1		0

1

2

2

3

3

4

4

0 0 12 0

h = 12+3=15

а б

Рис. 3.4. (а) Приведена матриця вартості після викреслювання рядка 3 і стовпчика 5 і встановлення з₅₃=оо; (б) приведення матриці вартості зображеної у частині (а).

На даній стадії нам удалося скоротити розмір матриці вартості, розглянутої у вершині {3, 5}. Крім того, якщо ми зможемо знайти тур з множини {3.5} вартістю, меншої чи рівній 62, тоді не потрібно проводити далі розгалуження й обчислення границь у вершині {3, 5}. У цьому випадку будемо говорити, що вершина {3, 5} у дереві відпрацьована. Тоді наступною метою може бути розгалуження з вершини {3, 5} у надр знайти тур з вартістю в межах 49<с<62.

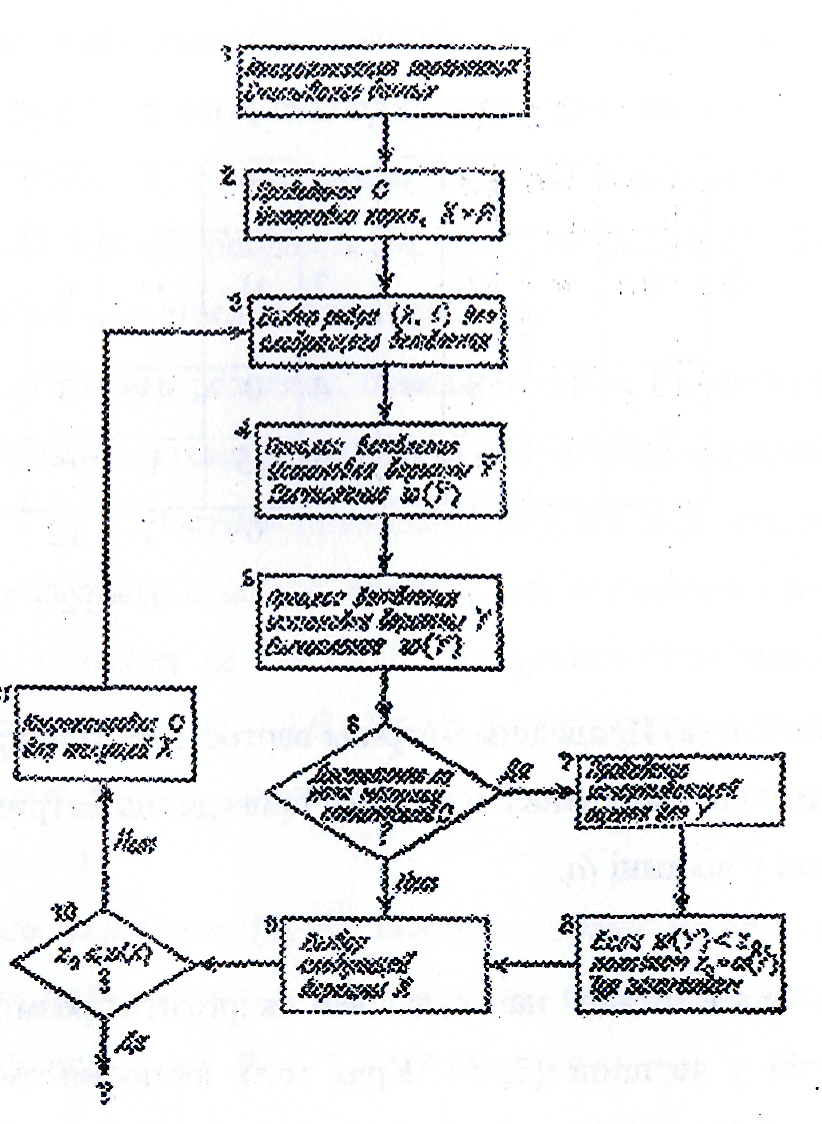
Рис. З.5. Блок-схема алгоритму гілок та меж.

В основних рисах блок-схема цього алгоритму гілок та меж показана на Рис. 3.5. Незабаром ми доповнимо цю схему рядом важливих деталей. Тут використовуються наступні позначення. Буква X позначає поточну вершину на дереві пошуку, a w(X) — відповідну нижню границю. Вершини, що випливають безпосередньо за X, назвемо Y і Y; вони вибираються розгалуженням по деякому ребру (к, 1). Символ Zo позначає вартість найдешевшого туру, відомого на даний момент. У початковий момент z₀= .

Блок 1. Установлення-початкових значень перемінних, чи ініціалізація.

Б лок 2. Перше приведення — це безпосередня реалізація описаної раніше процедури-,

Блок 3. Вибір наступного ребра розгалуження (к, 1) визначає множини Y і Y, що безпосередньо випливають за поточним X. Ребро (к, 1) потрібно вибирати так, щоб спробувати одержати велику по величині нижню межу на множині Y={k, І}, що полегшить проведення оцінки для множини Y. Звичайно краще провести оцінку для Y, тому що розмір цієї множини і відповідна йому матриця вартості звичайно більше, ніж у Y (з матриці для Y викреслений рядок к і стовпець /). Можна сподіватися також, що Y с більшою імовірністю містить оптимальний тур.

Як застосувати ці ідеї до вибору конкретного ребра розгалуження (к, /)? У приведеній матриці вартості С`, зв'язаної с Х, кожен рядок і стовпець мають хоча б по одному нульовому елементі (якщо ні, те С` не цілком приведена). Можна припустити, що ребра, що відповідають цим нульової вартостям, будуть с більшою імовірністю входити в оптимальний тур, чим ребра с великими вартостями. Тому ми виберемо одне з них. Нехай ребро (і, j) має Cij==0 у С`. Ми хочемо, щоб у Y={i, j} була як можливо велика нижня межа. Згадуючи метод обчислення нижньої межі для {3, 5} у нашому прикладі, ми бачимо, що для 7 ця межа задається у вигляді

w (Y) = w(X)+(найменша вартість у рядку і, не включаючи

Сц) +(иайменша вартість у стовпчику], не включаючи cj).

Отже, із усіх ребер (і, j) с с_г;=0 у поточній матриці С ми вибираємо те, що дає найбільше значення для w(Y). Нехай це буде ребро (к, 1).

Тому більш докладний опис вибору, представленого блоком 3, має насту іший вид:

Крок 1. Нехай S — множина ребер (i,j), таких, що сij=0 у поточній матриці вартості С.

Крок 2. Покладемо Dj рівним найменшої вартості в рядку і, крім cij, плюс найменша вартість у стовпчику j, крім с_ч. Обчислюємо Dij для усіх (і, /)єS.

Крок 3. Вибираємо наступне ребро розгалуження (к, 1) з умови

Розглянемо знову задачу с п'ятьма містами, зображену на Рис. 17. З приведеної матриці С видно, що перше значення X, корінь R, має w(X)-47. Застосовуючи підалгоритм, описаний вище, знаходимо наше перше ребро розгалуження в такий спосіб:

Крок 1. S={(1, 2), (2,1), (3, 5), (4, 5), (5, 3), (5, 4)}

Крок 2. D₁₂=2+l=3 D_2]=12+3=15 D₃₃=2+0=2 D₄₅=3+0=3 D_e=0+12=12 D₆₄=0+2=2

Крок 3. Вибираємо ребро (k, 1)= (2, 1), тому що D₂i — це максимальний елемент множини {Dц}.

Блок 4. Визначаємо вершину Y, що випливає заХ, точно так само, як ми робили раніш.

У розглянутому прикладі Х=R і Y={2, 1}, таким чином це множина усіх турів, що не містять ребро (2,1). Обчислюємо нижню границю w(Y) так само, як у блоці 3,

w(Y} = w(X) +D'u i w({2, 1}) = 47 + 15 = 62.

Блок 5. Вершині Y, що випливає заХ, відповідає підмножині турів з Х, що містять те ребро (к, /), що обрана в блоці 3. У розглянутому прикладі Y={2, 1}. При обчисленні w(Y) необхідна відома обережність. Докладний підалгоритм має наступний вид:

Крок 1.3С виключаємо рядок k і стовпець /.

Крок 2. Усі тури множини, представленого вершиною Y, містять декілька (може бути, жодного) з раніше обраних ребер, крім ребра (к, l). Ребро (к, l) чи буде ізольовано від цих інших ребер, чи буде частиною шляху, що включає деякі чи всі ці ребра. Нехай р і q — початкове і кінцеве міста цього шляху. Можливо, що р=к і (чи) q=l. Покладемо Cqp=oo. Ця міра охороняє від вибору ребра (q, p) у якості наступного для Y, а тим самим охороняє від формування замкнутого циклу довжини менше N. Такі цикли, звичайно, не дозволені при побудові туру. Є чи якісь випадки, у яких ми не думаємо Cqp= oo ?

Крок 3. Приводимо розглянуту матрицю С. Нехай h буде дорівнює сумі констант приведення.

Крок 4. Обчислюємо w(Y) по формулі w(Y)=w(X)+h.

Повертаючись до прикладу, викреслюємо рядок 2 і стовпець 1 з матриці С, показаної на Рис. 3.3. Тому що ребро (2, 1) — єдине обране ребро, маємо р=2, g=l і С₁₂=оо. Після цих кроків, що відповідають крокам 1 і 2 описаного вище підалгоритму, що поточна матриця показана на Рис. 3.6, а. Після приведення одержуємо матрицю, зображену на Рис. 3.6, б, з h =3 і w [(2, 1)] = =w(X)+ft=47+3=50. Поточний стан показаний на рівнях 0 і 1 на Рис. 3.7.

1

2

2 3 4 5 2 3 4 5

	15	3	2
14		2	0
44	18		0
1	0	0

	13	1	0 0
13		2	0 0
43	18		0 0
0	0	0

1

3

2

3

4

4

5

1 0 0 0

h = 2+1=3

а б

Рис 3.6. (а) Приведена матриця вартості після викреслювання рядка 2 і стовпчика 1 і встановлення з_І2=оо; (б) приведення матриці вартості, зображеної у частині (а),

Рис. 3.7. Дерево пошуку.

Блок 6. Зрештою ми повинні прийти до множин, які мають так мало турів, що ми можемо розглянути кожний з них і провести оцінку для цієї вершини без подальшого розгалуження. Блок 6 перевіряє, чи не прийшли ми вже до таких множин. Кожне ребро, про яке ми знаємо, що воно міститься у всіх турах з F, скорочує розмір С на один рядок і один стовпчик. Якщо у вихідній задачі було N міст, а поточна матриця С має розмір 2x2, то обрано уже N—2 ребер кожного туру Y. Тому множина Y містить якнайбільше два тури Таким чином, блок б перевіряє, чи є С матрицею розміру 2x2. Помітимо, що це, власне кажучи, дає відповідь на питання, поставлений наприкінці кроку 2 під час обговорення блоку 5.

Блоки 7 і 8. Блок 7 працює, тільки якщо С — матриця розмірів 2x2. У цьому блоці відшукується найдешевший тур у Y і його вага позначається через w(Y). У блоці 8 перевіряється, чи краще даний тур, чим поточний кращий з відомих турів. Якщо ні, то новий тур відкидається. Якщо так, то поточним кращим туром буде новий тур, і ми маємо z=w(Y).

Блок 9. Тепер потрібно вибрати наступну вершину X, від якої проводити розгалуження. Цей вибір досить очевидний. Вибираємо вершину, з якої в даний момент не виходять гілкиі і яка має найменшу нижню границю. Отже, даний блок складається з наступного подалгоритма:

Крок 1. Шукаємо множину S кінцевих вершин поточного дерева пошуку.

Крок 2. Нехай вершина X буде обрана так, що

w(X) = minw(v).

v S

У розглянутому прикладі:

Крок 1. S={{2,1},{2,1}}

Крок2. w({2,1})=62, w({2,1))=50. Тому Х={2,1}.

Блок 10. Блок 10 показує, чи повинні ми зупинитися. Якщо поточна межа дію нашого кращого туру Zo менше чи дорівнює w(X) — найменшої з недосліджених нижніх меж,— тоді ніяка з вершин, що випливають за X, не може містити кращого туру. Завдяки способу вибору X у блоці 9 кращий тур не може також міститися ні в який іншій з неоцінених кінцевих вершин. Тепер усе дерево пошуку оцінене, і ми зупиняємося. Якщо w(X)<Zo, пошук повинний бути продовжений. У нашому прикладі z₀= , тому пошук не припиняється.

Блок 11. У цій частиш алгоритму виходить відкоректована матриця вартості С для поточної вершини X. Процедура коректування наступна: Крок 1. Чи дорівнює множина X множині Y, що останній раз утворена в блоці 5? Якщо так, то поточна матриця С — це те, що нам потрібно, і ми повертаємося в блок 3. Саме це звичайно відбувається на рівні 2 дерева пошуку.

Крок 2. Установлюємо С вихідна матриця вартості.

Крок 3. Установлюємо S множина усіх пар (і, l), що повинні бути

ребрами в X}.

Крок4. Обчислюємо g=Z(i,j)_esCij.

Крок 5. Для кожної (і, j) є S викреслюємо рядок i і стовпчик j у С. Для кожного шляху, що проходить через (і, j), знаходимо початкове і кінцеве міста р і q і маємо с_чр=<х. У кожного ребра (к, /), забороненого для турів у X, маємо Сkl=оо.

Крок 6. Приводимо матрицю С. Маємо h рівним сумі констант приведення.

Крок 7. Обчислюємо w(X)=g+h. Kpoк 5 вносить незручність, тому що він зводиться до повторення того, що ми робили раніш. Очевидна альтернатива, здійснення якої зажадає великого обсягу пам'яті,— запам'ятовувати матриці С для кожної кінцевої вершини дерева. Як правило, це непрактично. У розглянутому прикладі ми просто виходимо з подалгоритма на кроці 1.

Продовжимо приклад. Зараз ми знаходимося в блоці 3, Х={2, 1}, W(X)=50, і дерево містить только рівні 0 і 1 (Рис. 3.7). Для визначення множин, що випливають за X, потрібно ребро (к, І). Придатна матриця С показана на Рис. 3.6, б. Використовуючи подалгоритм, описаний у блоці 3, маємо

Крок 1 S=((l, 5), (3, 5), (4, 5), (5, 2), (5, 3), (5, 4)}

D₁₅=1+0=1

D₃₅=2+0=2

D₄₅-l 8+0=18

D₅₂-13+0=13

D₅3=13+0=I3

D'₅₄=0+1 = 1

Крок 3. D₄₅=18 (у випадку декількох рівних вибираємо довільно). Таким чином, (к, /)⁼(4, 5).

Тепер установлюємо Y, використовуючи блок 4:

Y = {43} і W({43}) = W{2, 1}) + D₄₅ = 50+ 18 = 68.

Далі розглядаємо вершину Y={4, 5}. По-перше, викреслюємо з С рядок 4 і стовпчик 5. Тому що ребро (4, 5) не перетинається с ребром (2, 1), р=4 і q=5. Маємо С54=°с і приводимо С. Знаходимо, що h=3 і W(y)=50+h=53. Приведена матрица С показана на Рис.3.8,а. Нижня межа не зменшується при проходженні вглиб дерева.

Тепер ми знаходимося в блоці 6. Чи є поточна матриця С матрицею 2x2? Так як С — матриця-3x3, переходимо в блок 9. Підалгоритм блоку 9 виконується в такий спосіб:

Крок 1. S={{2,1},{4,5},{4,5}}

Крок 2 w({2,l})=62

w({4,5})=68

w({4,5})=53

Отже, Х=(4,5}.

1

2 3 4 1 2 3 4 5

	12	0
11		0
0	0

	0	15	3	2
		0	10	8
15	14		2	0
0	44	18		0
12	1	0	0

1

1

3

2

2

3

5

0

4

5

0 0 0

2 3

0 3 h= 2+1=3	11 h= 62
5	0 0

h= 11

0 0

а б в

Рис. 3.8. Додаткові приведені матриці вартостей для задачі на Рис. 3.1

У блоці 10 zo= , тому йдемо далі. У блоці 11 нам повезло, і ми виходимо на кроці 1. Знову переходимо в блок 3 з Х={4, 5}, w(X) =53, і матриця С редставлена на Рис. 3.8, а.

Ще один раз, і мета може бути досягнута! Підалгоритм блоку 3 дає наступне: Крок 1. S=((l, 4), (3,4), (5, 2), (5, 3)}.

Крок 2. D =12+0=12 d

D₃₄=l1+0=11

D₅₂= 11+0=11

D₅₃=12+0=12

К рок 3. D_kl=D₁₄=D₅₃=l 2. Ми довільно вибираємо (k, /)=(1, 4).

Тепер Y= {1,4} і w(y)= w({4,5}) +D`₁₄ = 53 + 12 = 65

Оскільки Y={1, 4}, з С викреслюємо рядок 1 і стовпець 4. Ребро (1, 4) разом с ребрами (2, 1) і (4, 5) утворить шлях. Тому р=2 і q=5. Занесемо с₅₂ = i приводимо поточну матрицю С. Знаходимо, що А=11 і w(Y)=53+h=64. На Рис. 23, 6 показана приведена матриця С.

Тепер ми знаходимося в блоці 6 с матрицею С розмірів 2x2. Блок видає тур знаступним порядком міст: 321453

і вартістю z=64. У блоці 8 маємо zo=64; тепер це поточний кращий тур. Чи всі ми зробили? Нам не треба розглядати вершини, що випливають за вершинами {4,5} і {ї^}, тому що їхні нижні межі більше ніж 64. Однак у блоці 10 ми бачимо, що в кінцевій вершині {2,1} нижня межа дорівнює 62<64. Отже, можливо, що тур з цієї підмножини може бути трохи краще, ніж той, який ми одержали. Таким чином, треба ще дещо зробити.

Ми знаходимо, що Х={2, 1}, z(X)=62, а матриця С, відкоректована р допомогою шдалгоритма блоку 11, має вид, як на Рис. 23, в. Далі у блоці З вибирається ребро

(4, 1) з D *, = 12 як наступне ребро розгалуження. У блоках 4 і 5 обчислюються w({4,l})=62+12=74 і w({4,1))=62. Необхідна ще одна ітерація.

Хоча здається, що тільки що побудований алгоритм працює дуже довго на нашему маленькому прикладі с п'ятьма містами, насправді це досить могутній інструмент. Ретельно виконана програма звичайно вирішує задачу комівояжера с 20—30 містами істотно швидше ніж за одну хвилину. Задачі с 40—50 містами часто можуть бути вирішені за цілком доступний час (менше 10 хв часу роботи центрального процесора).

Існують різні евристичні прийоми, що можуть прискорити цей основний алгоритм гілок та меж. Алгоритм "Жадібний комівояжер2" можна використовувати як початковий етап для алгоритму гілок та меж з даного розділу. Як ми бачили при побудові цього останнього алгоритму, може знадобитися якийсь час, перш ніж буде знайдені перший повний тур і ш₀ стане реалістичною оцінкою вартості оптимального туру. Якщо на початку роботи алгоритму відомий досить гарний тур, скажемо отриманий алгоритмом 12, тоді z₀ c самого початку встановлюється на досить низький

рівень. У цьому випадку будь-яка вершина на дереві пошуку, нижня межа якої виявляється чи більше рівної z , відразу може вважатися дослідженою. Таким чином, можна значною мірою уникнути марного пошуку при роботі точного алгоритму.

Цей алгоритм вважався одним із кращих для задачі комівояжера майже до 1970 p. C тих пір з'явилися більш швидкі алгоритми. Про усіх більш-менш ефективних алгоритмах гілок та меж відомо, що їхня трудомісткість у гіршому випадку є експонентної.

Контрольні запитання.

1. Що означає гілка для методу меж та гілок?

2. Що є межею для методу меж та гілок?

3. Яку структуру даних використовують для методу меж та гілок?

4. Що означає приведення матриці в методі меж та гілок для задачі про комівояжера?

5. Сформулюйте алгоритм методом меж та гілок для задачі про комівояжера.

6. Розв'яжіть задачу про комівояжера методом меж та гілок для несиметричної матриці 4x4.

7. Яка робоча функція методу меж та гілок.