Полные дифференциалы высших порядков

Пусть функция определена в некоторой области и точка

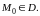
Определение. Функция переменных называется 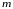раз дифференцируемой в точке 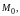если в этой точке дифференцируемы она сама и все ее частные производные до 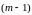-го порядка включительно.

Определение. Функция переменных называется раз дифференцируемой в открытой облас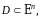ти если она раз дифференцируема в каждой точке области.

Рассмотрим функцию

где и - независимые переменные. Если эта функция дифференцируема, то ее полный дифференциал имеет вид

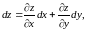
где 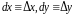- произвольные приращения независимых переменных, то есть произвольные числа не зависящие от и . На этом основании будем изменять и , зафиксировав 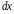и 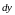(то есть оставляя их постоянными). Тогда 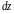станет функцией двух переменных и .

Если функция дифференцируема два раза (то есть она дифференцируема вместе со своими частными производными), то и ее полный дифференциал будет дифференцируемой функцией и в свою очередь будет иметь полный дифференциал. Полный дифференциал от полного дифференциала функции называется полным дифференциалом (дифференциалом) второго порядка функции и обозначается 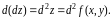Найдем его

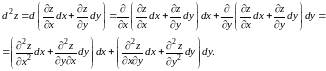
После преобразований, считая, что получим

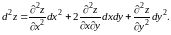(8.21)

Пример. Найти 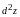для функции 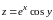в точке

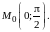
Решение. Находим первые и вторые частные производные

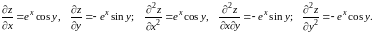По формуле (8.21)

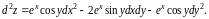
Теперь

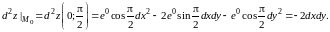
Если функция дифференцируема трижды (т. е. дифференцируема вместе со своими частными производными до второго порядка включительно), то 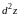будет дифференцируемой функцией, а ее полный дифференциал называется полным дифференциалом третьего порядка функции . Обозначение

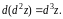
Аналогично предыдущему можно показать, что

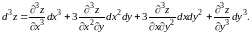(8.22)

Для формул (8.21) и (8.22) удобна следующая символическая запись:

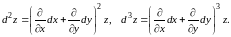
Здесь символы 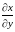и 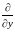рассматриваются как «множители», и формула бинома Ньютона с последующим условным умножением на приводит соответственно к формулам (8.21) и (8.22).

Вообще, если функция дифференцируема раз, то полный дифференциал -го порядка этой функции определяется равенством

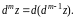
Методом математической индукции доказывается, что для любого справедлива формула

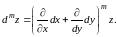
Если аргументы и функции не независимы, а являются функциями некоторой переменной , то 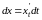и 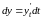тоже будут функциями (их нельзя считать постоянными). Выражения для полных дифференциалов высших порядков такой функции (сложной функции) будут отличаться от полученных. Следовательно, полные дифференциалы высших порядков свойством инвариантности формы по отношению к аргументам не обладают.

Все сказанное о дифференциалах высших порядков для функции двух переменных легко обобщается и на функции большого числа переменных. Так, например, для функции трех независимых переменных полный дифференциал 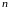-ого порядка находится с помощью формулы

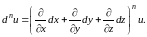(8.23)

Пример. Найт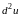и , если .

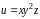Решение. При из (8.23) имеем

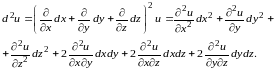
Находим первые частные производные

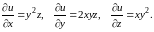
Теперь

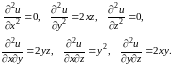
Окончательно

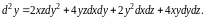
Решение задач

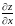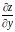Задача 1. Найти частные производные и функции

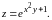
Решение. Находим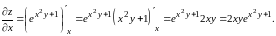 Вычисляя 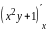, воспользовались тем, что при нахождении частной производной по переменная считается постоянной. Аналогично, полагая переменную постоянной, получим

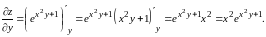
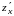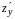Задача 2. Найти и функции

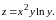
Решение. Находим , считаем величиной постоянной. Выносим за знак производной и получаем 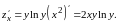При нахождении за знак производной выносим 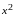и , дифференцируем как произведение функций:

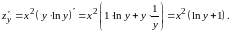
Задача 3. Найти частную производную по от функции трех переменных 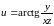в точке

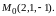
Решение. Считая и , а, следовательно, и 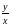постоянными и учитывая правила дифференцирования сложной функции одной переменной, получим:

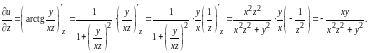
Вычислим значение

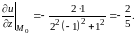
Задача 4. Найти полный дифференциал функции 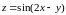в точке

Решение. Если функция дифференцируема в точке , то ее полный дифференциал находится по формуле 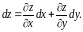Найдем частные производные 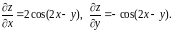Подставляя в формулу, получим

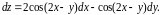
Находим значение в точке . Получим

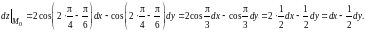
Задача 5. Найти все частные производные второго порядка для функции

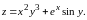
Решение. Чтобы найти частные производные второго порядка, сначала нужно найти частные производные первого порядка. В нашей задаче 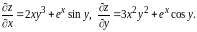Теперь находим частные производные второго порядка

Заметим, что 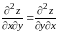, что и следовало ожидать, так как если смешанные частные производные непрерывны, то результаты дифференцирования не зависят от порядка дифференцирования.

Задача 6. Найти 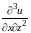для функции .

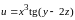Решение. Сначала находим 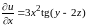. Далее 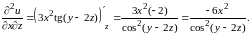и наконец, 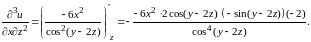После преобразований получаем ответ:

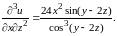
Задача 7. Найти полный дифференциал функции , заданной неявно уравнением 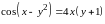и его выражение в точке .

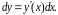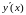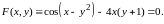Решение. Дифференциал функции (как функции одной переменной) равен Найдем функции, заданной неявно по формуле (8.19). Для этого запишем уравнение в виде Тогда

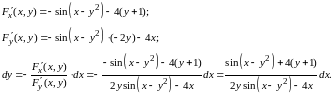
В точке имеем 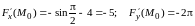и ответ