4. Квадратура круга, удвоение куба, трисекция угла, теорема Ферма, проблема четырех красок.

В задаче о квадратуре круга требуется построить циркулем и линейкой квадрат, равновеликий данному кругу.           Вероятно, задача была известна уже за две тысячи лет до н. э. в Древнем Египте и Вавилоне. Но первая прямая ссылка на неё относится к V в. до н. э. По свидетельству древнегреческого историка Плутарха, философ Анаксагор, коротая время в тюрьме, пытался квадрировать круг, т. е. превратить его в  равновеликий квадрат. Если считать радиус данного круга равным 1, то сторона искомого квадрата должна составить квадратный корень из числа пи. Надежды «квадратурщиков» подогревались существованием криволинейных фигур, квадрируемых циркулем и линейкой. Гиппократ Хиосский нашел одну из таких фигур, известную как «луночки Гиппократа».  Он нашёл и другие луночки, допускающие квадратуру, что, конечно, не помогло ему решить саму исходную задачу. Было предложено множество построений. В лучшем случае они давали приближённое значение числа пи с достаточно хорошей точностью. Однако, в отличие от приведённых выше решений двух других знаменитых задач, эти построения были принципиально приближёнными. Впрочем, авторы таких построений часто не сомневались в их абсолютной точности и горячо отстаивали свои заблуждения. Один из самых громких споров на эту тему произошёл в Англии между двумя выдающимися учёными XVII в. — философом Томасом Гоббсом и математиком Джоном Валлисом. В весьма почтенном возрасте Гоббс опубликовал около десяти «решений» задачи о квадратуре круга.             Итак, задача о квадратуре круга оказалась наиболее сложной из трех. Метод, использованный в двух других задачах, здесь не подошёл, так как число пи имеет совершенно другую природу, чем 2^1/3 или корни уравнений, к которым сводится трисекция. Только к 1822 г. Фердинанд Линдеман доказал, что число пи трансцендентно, т. е. не является корнем никакого многочлена с целыми коэффициентами. Значит, оно и не квадратично-иррационально, поскольку в противном случае было бы корнем какого-либо многочлена.             Так Линдеман наконец поставил точку в проблеме разрешимости посредством циркули и линейки последней из трёх классических задач древности.

Удвоение куба

В этой задаче требуется  построить циркулем и линейкой куб вдвое большего объёма, чем заданный.      Ребро искомого куба равно a·2^1/3, где а — ребро исходного куба. Если принять, что а= 1, то искомое ребро х есть корень уравнения X³ - 2 = 0. У данного уравнения нет рациональных, а значит, и квадратично-иррациональных корней. Следовательно, удвоение куба нельзя осуществить циркулем и линейкой. Примерно такое расуждение было применено в начале XIX в., когда был подготовлен необходимый для этого алгебраический аппарат. Считают, что задача об удвоении куба появилась во времена пифагорейцев, около 540 г. до н. э. Возможно, она возникла из задачи об удвоении квадрата, которую легко решить, опираясь на теорему Пифагора, — надо построить квадрат на диагонали данного квадрата. Согласно легенде, жители Афин, на которых боги ниспослали эпидемию чумы, отправили делегацию к оракулу на остров Делос за советом, как задобрить богов и избавиться от морового поветрия. Ответ был таков: «Удвойте жертвенник храма Аполлона, и чума прекратится». Жертвенник имел кубическую форму. Афиняне решили, что задание простое, и построили новый жертвенник, с вдвое большим ребром. Однако чума только усилилась, Вторично обратились к оракулу и получили ответ: «Получше изучайте геометрию». История умалчивает о том, как удалось умилостивить богов, но чума в конце концов покинула город. А задачу об удвоении куба стали называть делосской задачей. Известна и другая легенда. Греческий комментатор VI в. до н. э. сообщает о письме, предположительно написанном царю Птолемею I. В нём говорится, что царь Минос построил на могиле сына надгробие кубической формы, но остался недоволен размерами памятника и приказал удвоить его, увеличив вдвое ребро куба. Комментатор указывает на ошибку царя Миноса (площадь поверхности памятника в результате увеличилась в четыре, а объём — в восемь раз) и рассказывает, что тогда геометры попытались решить эту задачу. Но так и не сумев с ней справиться с помощью циркуля и линейки, греки попробовали применить другие инструменты, механизмы и даже специальные кривые. Гиппократ Хиосский, знаменитый геометр V в. до н. э., свёл удвоение куба к построению «двух средних пропорциональных» х и у для данных отрезков а и b, т.е. к. решению уравнений а : х = х : у = у : b (при b = 2а получаем х = а ·2^1/3). Эту идею удалось реализовать Платону около 340 г. до н. э. с помощью нетрадиционных чертёжных инструментов — двух прямых углов. Свои решения дали также крупнейшие древнегреческие математики Евдокс, Эратосфен, Аполлоний, Герон, Папп, и др. Никомед из Александрии (2 в. до н. э.) использовал для решения этой задачи особую кривую — конхоиду (слово «конхоидео в переводе с греческого означает «подобная раковине мидии»). Диоклес придумал для решения этой задачи замечательную кривую - циссоиду (от греч.«киссоидес» - «плющевидный»). Менехм примерно в 350 г. до н.э. решал задачу об удвоении куба, используя конические сечения — кривые, по которым плоскости пересекают конус. 

Трисекция угла

Несложно разделить любой угол с помощью циркуля и линейки на две, а некоторые углы - и на три равные части. Последняя операция называется  трисекцией угла.  Например, мы можем построить треть прямого угла, поделив пополам угол правильного треугольника, а проведя биссектрису в образовавшемся угле в 30°, получим угол величиной 15° — треть угла в 45°.  Есть и другие углы, для которых трисекция выполнима. Наверное, подобные построения и вселили надежду открыть способ трисекции любого угла посредством циркуля и линейки. Эту задачу пытались решить ещё в V в. до н. э. в Греции. Гиппий Элидский (около 420 г. до н, э.) для трисекции угла использовал кривую, впоследствии названную квадратрисой. Никомед с той же целью чертил свою конхоиду с полюсом О, основанием р и интервалом 2ОВ; она пересекает l в искомой точке Q. Французский математик П. Ванцель к 1837 г, первым строго доказал, что невозможно осуществить трисекцию циркулем и линейкой.         Пусть а = р/3. По известной формуле, cos р = 4cos³ а - 3cos а. Тогда для величины х = =2 cos р получается уравнение х³ - 3х - к = О, где к =2cos р. Геометрическая задача трисекции данного угла с циркулем и линейкой разрешима тогда и только тогда, когда полученное алгебраическое уравнение разрешимо в квадратных радикалах. Возьмём, например, р = 60°. Тогда уравнение примет вид  х³ - 3х - 1 = 0. Оно неразрешимо в квадратных радикалах, а потому и трисекция с помощью циркуля и линейки в данном случае невозможна. Тем более она невозможна в общем случае.        Интересно, что вообще для углов вида 360°/n с целым n трисекцию удаётся осуществить тогда и только тогда, когда n не делится на 3.

Теорема Ферма

Большой известностью во всём мире пользуется «Великая теорема Ферма» (она же – «Большая» или «Последняя»). Великой теоремой Ферма называется то заключение, которое было сделано им при чтении изданной Мезириаком «Арифметики» Диофанта. Это положение Ферма теперь формулируется как теорема в следующем виде: «Уравнение xⁿ + yⁿ = zⁿ не может быть решено в рациональных числах относительно x, y и z при целых значениях показателя n, больших 2» (общеизвестно, что при n=2 такие числа существуют, например, 3, 4, 5 – числа, которые, если являются длинами сторон, образуют знаменитый треугольник Пифагора). Справедливость этой теоремы подтверждается для многих частных случаев (при этом ещё не найдено ни одного опровержения), однако до сих пор она не доказана в общем виде, хотя ей интересовались и её пытались доказать многие крупные математики (в «Истории теории чисел» Диксона прореферировано более трёхсот работ на эту тему). В 1907 году в городе Дармштадте в Германии умер математик Вольфскель, который завещал 100000 марок тому, кто даст полное доказательство теоремы. Но премия эта до сих пор никому не выдана за отсутствием настоящего доказательства Большой теоремы Ферма. Элементарного доказательства Великой теоремы Ферма нет ни для одного показателя n  4. Случай, когда n = 3, был доказан Эйлером ещё в 1768 году. И тот потребовал ещё много лет, чтобы теория, которой необоснованно пользовался Эйлер при своём доказательстве, была доказана Гауссом. Доказательство теоремы Ферма для случая, когда n = 5, предложили в 1825 году почти одновременно Лежен Дирихле и Лежандр. Своё доказательство Дирихле опубликовал в 1828 году, но оно было очень сложным, и в 1912 году его упростил Племель. Для следующего простого показателя n = 7 теорема Ферма была доказана лишь в 1839 году Ламе. Доказательство Ламе было почти сразу же усовершенствовано Лебегом. В 1847 году Ламе объявил, что ему удалось найти доказательство теоремы Ферма для всех простых показателей n  3. Метод Ламе представлял собой весьма далёкое развитие идей Эйлера и основывался на арифметических свойствах чисел. Однако сразу же Лиувилль обнаружил в рассуждениях Ламе серьёзный пробел, чем опровергнул это доказательство. Ламе был вынужден признать свою ошибку. На ЭВМ, пользуясь идеями Куммера и Вандивера доказали справедливость теоремы Ферма для всех простых показателей n < 100000.

Проблема четырёх красок

Исторически понятие хроматического числа возникло с проблемой четырех красок. Проблема возникла в математике в середине 19 века. Первоначально вопрос формулировался так: сколько нужно красок для раскраски любой географической карты, при которой соседние страны раскрашены в разные цвета? Под географической картой понимается разбиение плоскости на конечное число связных областей, стран, границы которых состоят из замкнутых непрерывных линий без самопересечений, а соседними являются страны, имеющие общую границу ненулевой длины. Довольно очевидно, что четырех красок недостаточно. и вопрос формулировался обычно в более конкретном виде: достаточно ли четырех красок для раскраски любой географической карты? Это и есть проблема четырех красок. Положительный ответ на вопрос называется гипотезой четырех красок. Проблема раскраски географических карт сводится к проблеме (правильной) раскраски плоских графов. Проиллюстрируем это сведение картой, изображенной на рис.5.9.

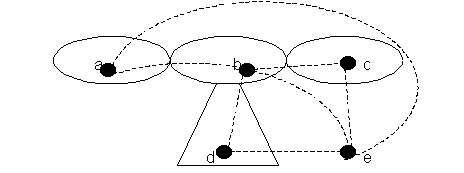
Рис.5.9

На рисунке изображена карта, имеющая пять стран (внешняя область - тоже страны). Внутри каждой страны зафиксируем точку, точки соединим ребром, если страны имеют общую границу. (На рис.5.9 ребра проведены пунктирными линиями). Ребра при этом можно провести так, чтобы они не пересекались, т.е. чтобы полученный граф был плоским. Ясно, что раскраска карты определяет правильную раскраску графа и обратно. Проблему четырех красок можно теперь сформулировать так: достаточно ли четырех красок для правильной раскраски плоского графа? Эта проблема вызвала большой интерес в математике. Есть свидетельства, что ей занимались известные математики Мебиус и де Морган. В 1880 году А. Компе опубликовал положительное решение проблемы четырех красок. Однако в 1890 году Р. Хивуд обнаружил ошибку в этом доказательстве. Одновременно он показал, что пяти красок достаточно для раскраски любого плоского графа (см. §4). После этого появлялось довольно много «доказательств» гипотезы четырех красок и «контрпримеров» к ней, в которых обнаруживались ошибки. В 1969 году Х. Хели свел проблему четырех красок к исследованию множества С так называемых конфигураций. Множество с является конечным. Но довольно большим (порядка нескольких тысяч). Несколькими годами позже, в 1976 году математикам К. Аппелю и В. Хейкену удалось показать. Что все конфигурации из множества С можно правильно раскрасить в четыре цвета. В возникающем при этом переборе существенно использовался компьютер. Такое решение проблемы четырех красок долгое время не признавалось многими математиками. Поскольку его сложно повторить. Однако сейчас практически общепризнано, что К. Аппелем и В. Хейкеном доказана гипотеза четырех красок.