3. Знакозмінні ряди. Абсолютна

І УМОВНА ЗБІЖНІСТЬ

Визначення 1. Знакозмінним рядом називається ряд, членами якого є числа довільного знака.

Нехай

(3.1)

деякий знакозмінний ряд.

Розглянемо ряд

, (3.2)

членами якого є абсолютні величини членів знакозмінного ряду (3.1). Ряд (3.2) є рядом із позитивними членами й до нього можна застосовувати ознаки, викладені вище.

Теорема 3.1. (Достатня ознака збіжності знакозмінного ряду) Якщо знакозмінний ряд (3.1) такий, що ряд (3.2) збігається, то й даний знакозмінний ряд також збігається. Ця ознака дає можливість судити про збіжність тільки деяких знакозмінних рядів. Вона є достатньою, але не необхідною: існують знакозмінні ряди, які самі збігаються, але ряди, складені з абсолютних величин їхніх членів, розбігаються. У зв'язку із цим вводиться поняття абсолютної й умовної збіжності знакозмінного ряду.

Визначення 2. Знакозмінний ряд (3.1) називається абсолютно збіжним, якщо сходиться ряд (3.2).

Визначення 3. Знакозмінний ряд називається умовно збіжним, якщо він сходиться, але не сходиться ряд з абсолютних величин .

Приклад1.

Ряд (3.3)

є знакозмінним. Складемо ряд з абсолютних величин цього ряду

(3.4)

Члени ряду (3.4) не перевершують відповідних членів збіжного ряду

,

тому ряд (3.4) збігається. Це означає, що ряд (3.3) абсолютно збігається.

Приклад2.

Розглянемо ряд (3.5)

Модулі членів цього ряду становлять гармонійний ряд

який розходиться. Отже, ряд (3.5) не є абсолютно збіжним. Однак, безпосереднім обчисленням суми цього ряду можна переконатися, що ряд (3.5) все одно збігається, тобто цей ряд - умовно збіжний.

3.1 Знакочередуючийся ряди. Ознака збіжності Лейбниця.

Визначення 4. Знакозмінний ряд називається знакочередуючимся, якщо його члени, які стоять поруч один до одного мають різні знаки. Знакочередуючийся ряд позначається .

Для знакочередуючихся рядів є досить загальна, чутлива й практична ознака збіжності, що належить Лейбницю.

Теорема 3.2. (Ознака Лейбниця) Якщо дано знакочередуючийся ряд , ( ), такий, що (тобто члени ряду монотонно не зростають) і , то даний ряд збігається і його сума .

Порядок дослідження знакозмінного ряду:

1. Складаємо ряд з модулів членів даного ряду й досліджуємо його на збіжність за однією з ознак для додатних рядів. Якщо отриманий ряд збігається, то збігається і даний ряд, причому абсолютно. Якщо ряд з модулів розбігається, то продовжуємо дослідження.

2. Якщо даний ряд знакочередуючийся, застосовуємо ознаку Лейбница. Якщо умови теореми 3.2 виконані, ряд збігається не абсолютно (умовно). Якщо ж умови не виконані, ряд розбігається.

Приклад1. Дослідити на збіжність ряд

Складемо ряд з модулів і досліджуємо його за ознакою Даламбера. Для даного ряду

;

Тоді

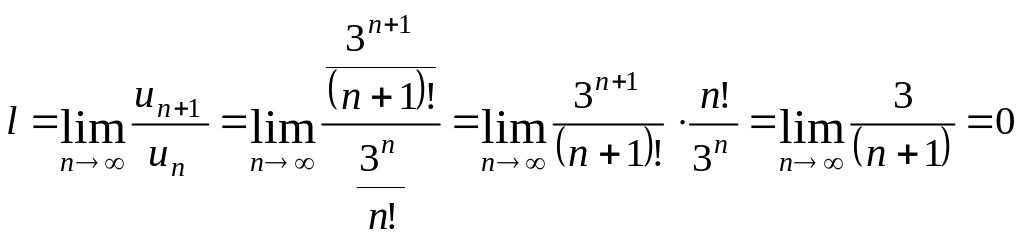
Так як <1, ряд збігається за ознакою Даламбера.

Виходить, вихідний ряд збігається абсолютно.

Приклад2. Дослідити на збіжність ряд

Складемо ряд з модулів і досліджуємо його за інтегральною ознакою Коши

Для цього ряду , і в цьому випадку

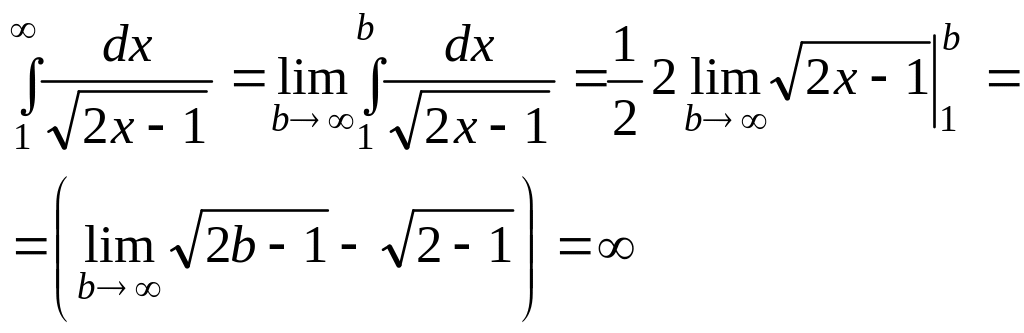
виходить, невласний інтеграл розбігається, отже, ряд з модулів не збігається.

До даного ряду застосуємо ознаку Лейбниця:

, .

Отже, вихідний ряд збігається умовно.