
- •1. Пряма на площині. Площина і пряма в просторі. Взаємне розміщення площин, прямих і площин в просторі.
- •4. Поверхні другого порядку
- •5. Метричні, псевдометричні, ультраметричні простори. Приклади.
- •6. Границя послідовності в метричному просторі. Повнота і поповнення
- •7.Точки дотику множини в метричному та топологічному просторі. Замкнені множини та замикання множини.
- •8. Внутрішні точки множини в метричному та топологічному просторі.
- •9.Неперервні відображення метричних просторів. Рівносильність означень за Гейне та за Коші
- •10. Поняття топології і способи її задання: метрика, база, передбаза.
- •11.Аксіоми відокремленості.Гаусдорфові, регулярні та нормальні простори.
- •12. Різновиди зв’язності та співвідношення між ними.
- •13. Неперервні відображення топологічних просторів.
- •14. Компактні простори і множини. Збереження компактності замкненими підпросторами і неперервними образами. Компактність відрізка. Компакти у скінченновимірних евклідових просторах.
- •15. Способи побудови нових топологічних просторів: підпростори, топологічні суми, фактор-простори, добутки.
- •16. Перша і друга квадратичнa форми поверхні.
- •17. Формули Френе для просторових кривих.
15. Способи побудови нових топологічних просторів: підпростори, топологічні суми, фактор-простори, добутки.
Озн. Якщо
![]() - фіксована підмножина множини
,
то слідом довільної підмножини
- фіксована підмножина множини
,
то слідом довільної підмножини
![]() на
називаємо перетин
на
називаємо перетин
![]() .
Для довільної топології
на множині
сліди всіх
.
Для довільної топології
на множині
сліди всіх![]() на
довільній фіксованій підмножині
на
довільній фіксованій підмножині
![]() утворюють деяку топологію
утворюють деяку топологію
![]() на
.
Кажемо, що топологія
індукована на
топологією
на
.
Зауважимо, що на
може
бути задана довільна топологія
на
.
Кажемо, що топологія
індукована на
топологією
на
.
Зауважимо, що на
може
бути задана довільна топологія
![]() ,
не пов’язана з топологією
на
.
Якщо ж
збігається з індукованою топологією
,
то топологічний простір
,
не пов’язана з топологією
на
.
Якщо ж
збігається з індукованою топологією
,
то топологічний простір
![]() називається підпростором топологічного
простору
називається підпростором топологічного
простору
![]() ,
а
- топологією підпростору.
,
а
- топологією підпростору.
Твердження. Якщо
- підпростір
![]() ,
а
- підпростір
,
а
- підпростір
![]() ,
то
- підпростір
.
,
то
- підпростір
.
Доведення.
З
![]() .
Якщо
- відкрита в
,
то
.
Якщо
- відкрита в
,
то
![]() ,
де множина
відкрита в
.
Для неї існує така відкрита в
,
де множина
відкрита в
.
Для неї існує така відкрита в
![]() множина
,
що
множина
,
що
![]() .
Тоді
.
Тоді
![]() ,
отже, кожна відкрита в
множина є слідом відкритої множини в
.
З другого боку, якщо
відкрита в
,
то
,
отже, кожна відкрита в
множина є слідом відкритої множини в
.
З другого боку, якщо
відкрита в
,
то
![]() - відкрита в
,
а
- відкрита в
,
а
![]()
![]() - відкрита в
.
- відкрита в
.
Диз’юнктне об’єднання
з такою топологією називається
топологічною сумою диз’юнктних просторів
і позначається
![]() або
або
![]() .
Топологічну суму
.
Топологічну суму
![]() диз’юнктних просторів
диз’юнктних просторів
![]() вважаємо топологічною сумою довільних
просторів.
вважаємо топологічною сумою довільних
просторів.
Озн. Добуток
![]() сім’ї множин
- це множина всіх таких функцій
сім’ї множин
- це множина всіх таких функцій
![]() ,
що
,
що
![]() для
кожного
для
кожного
Озн.
Відношення еквівалентності
![]() на топологічному просторі
задає сюр’єктивне фактор відображення
на топологічному просторі
задає сюр’єктивне фактор відображення
![]() з
в фактор-множину
з
в фактор-множину
![]() .
Множина
з фактор-топологією, заданою
та
називається фактор-простором простору
за відношенням
і позначається
.
Множина
з фактор-топологією, заданою
та
називається фактор-простором простору
за відношенням
і позначається
![]() або
.
або
.
16. Перша і друга квадратичнa форми поверхні.
Параметризована поверхня –
це довільне відображення
![]() з деякої області U
R2 у
трьохвимірний простір R3.
Поверхня задана трьома числовими
функціями
з деякої області U
R2 у
трьохвимірний простір R3.
Поверхня задана трьома числовими
функціями
![]() .
Якщо ці функції належать до
деякого класу гладкості, то вважаємо,
що і поверхня належить до цього класу.
Надалі вважаємо, що x,
y, z,
неперервно-диференційовні по
u і v.
Маємо частинні похідні
.
Якщо ці функції належать до
деякого класу гладкості, то вважаємо,
що і поверхня належить до цього класу.
Надалі вважаємо, що x,
y, z,
неперервно-диференційовні по
u і v.
Маємо частинні похідні
![]() .
Це означає, що для u=u0+u,
v=v0+v
маємо
.
Це означає, що для u=u0+u,
v=v0+v
маємо
![]() .
Але рівняння
.
Але рівняння
![]() при фіксованих
при фіксованих
![]() .
Рівняння параметрично задає площину,
яка проходить через
.
Рівняння параметрично задає площину,
яка проходить через
![]() покриття паралельно до
покриття паралельно до
![]() і
і
![]() .
Зокрема, рівність
.
Зокрема, рівність
![]() визначає площину, що проходить через
точку поверхні
визначає площину, що проходить через
точку поверхні
![]() паралельно
до
паралельно
до
![]() і
і
![]() .
Отже, поверхня відхиляється від цієї
площини на безмежно малу величину, меншу
ніж першого порядку малості. Отже, ця
площина є дотичною. Вивчимо відстань d
між точками
.
Отже, поверхня відхиляється від цієї
площини на безмежно малу величину, меншу
ніж першого порядку малості. Отже, ця
площина є дотичною. Вивчимо відстань d
між точками
![]() та
та
![]() ,
де u=u0+u,
v=v0+v
- безмежно малі. Але
,
де u=u0+u,
v=v0+v
- безмежно малі. Але
![]()
+
![]() .
Вираз називають першою квадратичною
формою і є наближеним значенням квадрата
переміщення по поверхні при малій
змінній параметра з точністю до малих
порядку вищого, ніж другий. Кажуть, що
перша квадратична форма визначає метрику
на поверхні. З її допомогою можна знайти
довжину будь-якої кривої на поверхні.
Нехай в області U
маємо криву u=u(t),
v=v(t),
atb.
Якщо підставити цю криву у функцію
.
Вираз називають першою квадратичною
формою і є наближеним значенням квадрата
переміщення по поверхні при малій
змінній параметра з точністю до малих
порядку вищого, ніж другий. Кажуть, що
перша квадратична форма визначає метрику
на поверхні. З її допомогою можна знайти
довжину будь-якої кривої на поверхні.
Нехай в області U
маємо криву u=u(t),
v=v(t),
atb.
Якщо підставити цю криву у функцію
![]() ,
яка визначає поверхню, то отримаємо
криву по поверхні. Тоді довжина кривої
рівна:
,
яка визначає поверхню, то отримаємо
криву по поверхні. Тоді довжина кривої
рівна:
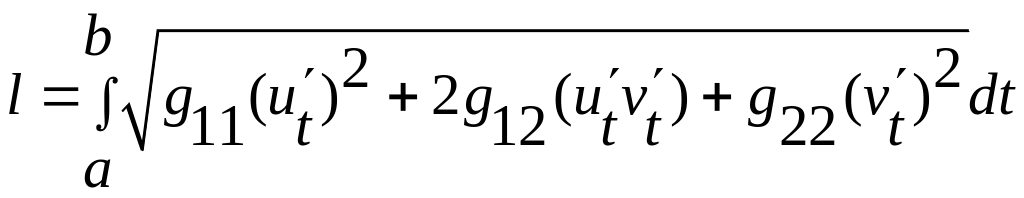 .
Також можна обчислити площу поверхні:
.
Також можна обчислити площу поверхні:
 .
.
Друга квадратична форма
Поверхню можна наблизити
точніше, якщо крім членів першого порядку
використати член другого порядку
![]() – формула Тейлора.
Визначимо відхилення точки поверхні
від дотичної площини. Для цього оберемо
нормальний вектор
– формула Тейлора.
Визначимо відхилення точки поверхні
від дотичної площини. Для цього оберемо
нормальний вектор
![]() ,
,
![]() .
.
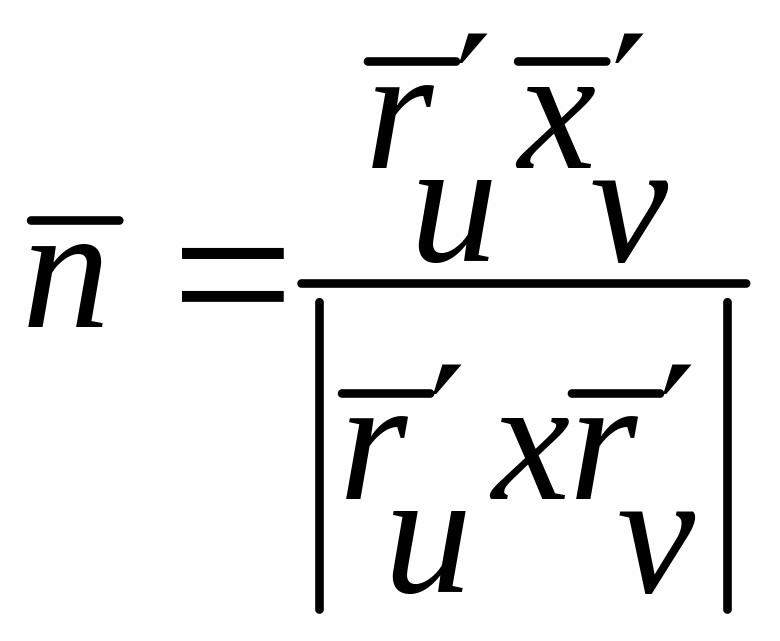 .
.
![]()
+![]() .
.
Отже, з точністю до нескінченно
малих другого порядку відхилення точки
від дотичної площини рівне
![]() - друга квадратична форма. Оскільки
перша кв. форма є наближеним значенням
квадрата відстані, вона є додатньовизначеною,
тому
- друга квадратична форма. Оскільки
перша кв. форма є наближеним значенням
квадрата відстані, вона є додатньовизначеною,
тому
![]() .
Рівність може досягатись тільки в точках
де порушується гладкість поверхні (в
особливих точках). Друга кв. форма не
обов’язково є знаковизначеною і може
мати різні властивості залежно від
розташування поверхні відносно дотичної
площини.
.
Рівність може досягатись тільки в точках
де порушується гладкість поверхні (в
особливих точках). Друга кв. форма не
обов’язково є знаковизначеною і може
мати різні властивості залежно від
розташування поверхні відносно дотичної
площини.
