2. Функциональные уравнения Беллмана

Как отмечалось выше, в основе динамического программирования лежит принцип оптимальности, указывающий на процедуру построения оптимального управления. Так как оптимальной стратегией может быть только та, которая одновременно оптимальна и для любого количества оставшихся шагов, ее можно строить по частям: сначала для последнего этапа, затем для двух последних, для трех и т.д., пока не придем к первому шагу. Отсюда принцип оптимальности связан со вторым принципом – погружения, согласно которому при решении исходной задачи ее как бы погружают в семейство подобных ей и решают для одного последнего этапа, для двух последних и т.д., пока не получат решение исходной задачи.

Дадим математическую формулировку принципа оптимальности для задачи с аддитивным критерием оптимальности. Для простоты будем считать, что начальное и конечное состояния системы заданы. Обозначим через значение функции цели на первом этапе при начальном состоянии системы и при управлении , через  соответствующее значение функции цели только на втором этапе, …, через  на -ом этапе, …, через  на -ом этапе. Очевидно, что

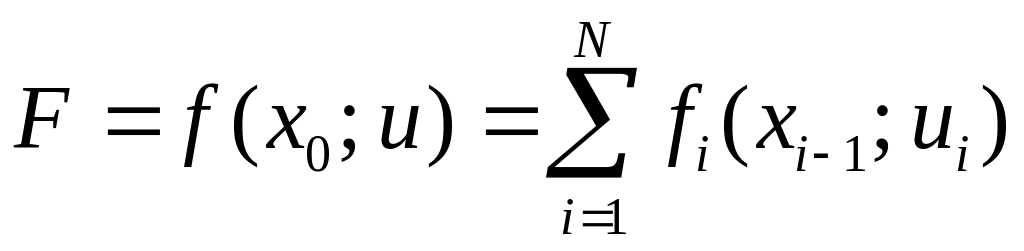. (2.1)

Надо найти оптимальное управление , такое, что доставляет экстремум целевой функции (2.1) при ограничениях .

Для решения этой задачи погружаем ее в семейство подобных. Введем обозначения. Пусть  соответственно области определения для подобных задач на последнем этапе, двух последних и т.д.;  область определения исходной задачи. Обозначим через , , …, , …, соответственно условно-оптимальные значения функции цели на последнем этапе, двух последних и т.д., на последних и т.д., на всех этапах.

Начинаем с последнего этапа. Пусть  возможные состояния системы на начало -го этапа. Находим

. (2.2)

Для двух последних этапов получаем

. (2.3)

Аналогично

, (2.4)

......................................................................

, (2.5)

......................................................................

. (2.6)

Выражение (2.6) представляет собой математическую запись принципа оптимальности. Выражение (2.5) – общая форма записи условно-оптимального значения функции цели для оставшихся этапов. Выражения (2.2) – (2.6) называются функциональными уравнениями Беллмана. Отчетливо просматривается их рекуррентный (возвратный) характер, т.е. для нахождения оптимального управления на шагах нужно знать условно-оптимальное управление на предшествующих этапах и т.д. Поэтому функциональные уравнения называют рекуррентными (возвратными) соотношениями Беллмана.

3. Задача распределения ресурсов

Задачу распределения ресурсов можно сформулировать следующим образом.

Пусть на реконструкцию и модернизацию основного производства объединению выделяется некоторый объем материальных ресурсов . Имеется предприятий, между которыми нужно распределить данный ресурс. Обозначим через прибыль, которую приносит выделение -му предприятию единиц ресурса. Предполагается, что размер прибыли зависит как от выделенного количества ресурса, так и от предприятия. Причем констатируется, что: прибыль, получаемая каждым предприятием, измеряется в одних и тех же единицах; прибыль, получаемая любым из предприятий, не зависит от того, какое количество этого ресурса выделено другим предприятиям; общая прибыль объединения состоит из прибылей отдельных предприятий.

Исследования функции показывают, что она обладает следующими особенностями:

1. небольшое количество выделенного ресурса не приносит сколько-нибудь ощутимого эффекта (прибыли);

2. для каждого предприятия существует момент, начиная с которого дальнейшее увеличение данного ресурса не эффективно.

Чтобы решить задачу распределения ограниченных ресурсов, применим аппарат функциональных уравнений Беллмана.

Сформулированные выше предположения приводят к функции цели:

. (3.1)

Задача оптимального распределения возникает оттого, что имеется ограниченный объем ресурсов , т.е.

. (3.2)

Сначала идет погружение в семейство подобных задач распределения. Вместо решения одной задачи с заданным объемом ресурсов и фиксированным числом предприятий рассмотрим их семейство, в которых объем выделенного ресурса может меняться от нуля до ( ) и число предприятий – от 1 до . Статическая задача распределения при таком подходе приобретает динамический характер. Введем последовательность функций , где  это максимальная прибыль, если бы ресурс был выделен только одному первому предприятию,  максимальная прибыль, полученная при условии, что ресурс был распределен двум предприятиям, и т.д. Пусть, наконец,  максимальная прибыль, полученная от распределения ресурса между предприятиями. Очевидно, что .

В двух случаях элементы последовательности имеют особенно простой вид:

1. ;

2. .

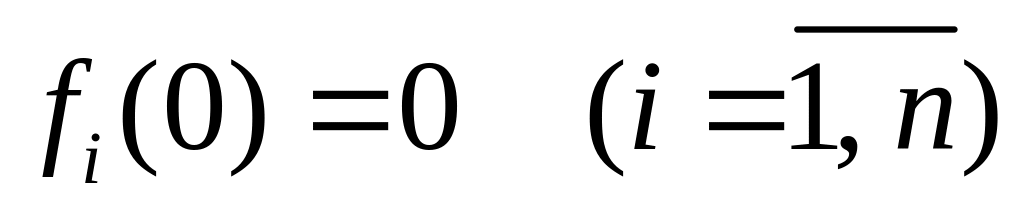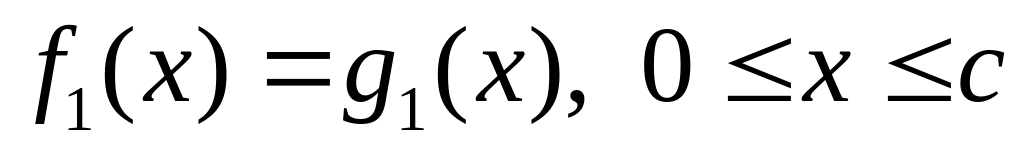Пусть ресурс распределен между двумя предприятиями. Если  объем ресурса, выделенного второму предприятию, то его прибыль составит . Оставшийся ресурс распределяется наилучшим образом. Общая прибыль для двух предприятий составит

.

Рассуждая аналогично, найдем рекуррентное соотношение, связывающее и для произвольных значений . В самом деле, пусть  количество ресурса, выделяемого для -го предприятия. Тогда, каково бы ни было значение , согласно принципу оптимальности, оставшийся ресурс распределяется между остальными предприятиями наилучшим образом. Так как известно, то

.

Решение исходной задачи получим при , , т.е. из рекуррентного соотношения

,

где .

На последнем этапе достигается максимальное значение функции цели и оптимальный объем ресурса, выделенного -му предприятию, т.е. .

Затем процесс вычислений просматривается в обратном порядке. Зная , находим  объем ресурса, подлежащего распределению между оставшимися предприятиями. Так как раньше найдено значение

,

отсюда находим и, следовательно, и т.д. Продолжая процесс к началу, определяем . Тем самым будет завершено определение оптимального плана распределения ограниченного ресурса.

Пример 3.1. Для реконструкции и модернизации производства выделены денежные средства в объеме 100 тыс. дол., которые следует распределить между четырьмя цехами. По каждому из цехов известен возможный прирост выпуска продукции в зависимости от выделяемой ему суммы ( ) возможные значения и приведены в таблице. Требуется:

1) основываясь на принципах динамического программирования, построить математическую модель поставленной задачи в виде функциональных уравнений Беллмана;

2) найти оптимальное распределение средств, обеспечивающее максимальный прирост выпуска продукции.

Выделяемые денежные средства, тыс. дол.	Прирост выпуска продукции по каждому цеху
0 20 40 60 80 100	0 9 18 24 44 59	0 11 19 30 38 59	0 16 32 40 69 73	0 13 27 44 57 70

Решение. 1) В данной задаче система представляет собой предприятие из 4-х цехов, в которое вложена сумма . Состояния и управления системы однозначно взаимосвязаны – это способы распределения суммы между цехами. Состояния системы искусственно разобьем на этапы: начальный (нулевой), первый, второй и третий этапы соответственно означают, что сумма распределена между четырьмя цехами, тремя цехами, двумя цехами и вся сумма выделена одному цеху. Нумерацию этапов удобно проводить в обратном порядке: третьему этапу соответствует , второму этапу  , первому – и начальному – .

Функциональные уравнения Беллмана имеют вид:

,

где  количество цехов,

 выделяемые средства,

 общий прирост выпуска продукции,

 прирост выпуска продукции каждого цеха в зависимости от выделенной ему суммы.

2) Пусть , т.е. предположим, что все имеющиеся средства выделяются на реконструкцию и модернизацию одного цеха, например, цеха № 1. Тогда функциональное уравнение Беллмана имеет вид:

,

где  прирост выпуска продукции по цеху № 1 в зависимости от выделенной суммы .

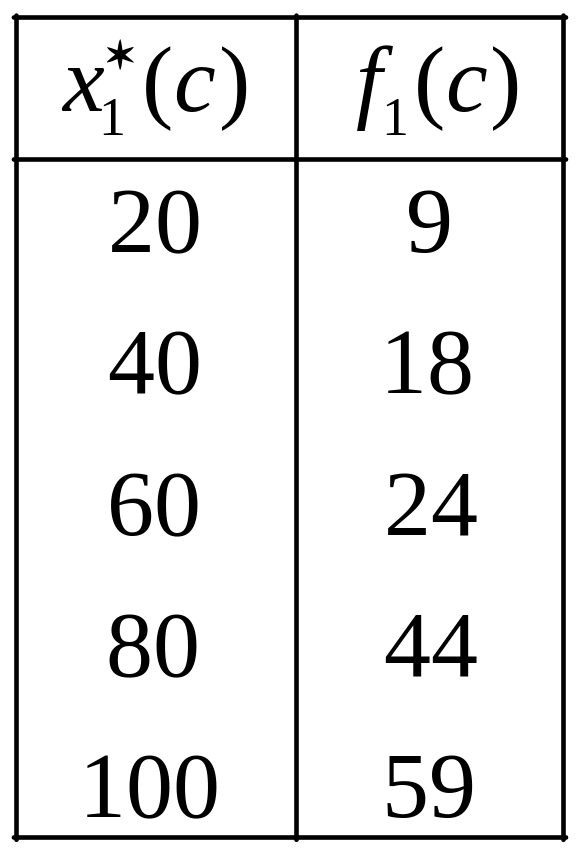
В зависимости от выделенной суммы получаем значения функции , которые заносим в таблицу 1.

Таблица 1.

.

Пусть , т.е. средства вкладываются в два цеха. Уравнение Беллмана имеет вид:

,

где  прирост выпуска продукции по цеху № 2 в зависимости от выделенной суммы .

Составляем таблицу 2 для всех возможных комбинаций и .

Таблица 2.

.

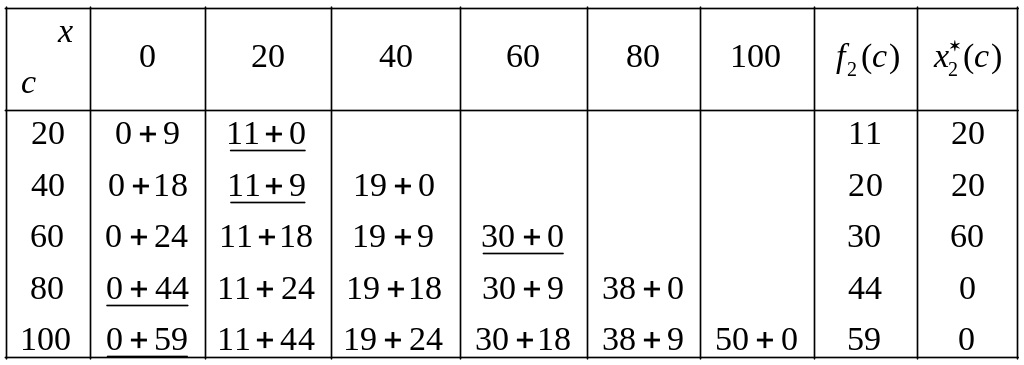В каждую клетку записывается сумма , где первое слагаемое берется из условия, а второе – из таблицы 1. В двух последних столбцах проставлены максимальный по строке прирост продукции (значения в таблице по строкам подчеркнуты) и соответствующая сумма средств, выделяемая второму цеху .

Пусть , т.е. средства вкладываются в три цеха. Уравнение Беллмана имеет вид:

,

где  прирост выпуска продукции по цеху № 3 в зависимости от выделенной суммы .

Составляем таблицу 3 для всех возможных комбинаций и .

Таблица 3.

.

В каждую клетку записывается сумма , где первое слагаемое берется из условия, а второе – из таблицы 2. В двух последних столбцах проставлены максимальный по строке прирост продукции и соответствующая сумма средств, выделяемая второму цеху .

Пусть , т.е. средства вкладываются в четыре цеха. Уравнение Беллмана имеет вид:

,

где  прирост выпуска продукции по цеху № 4 в зависимости от выделенной суммы .

Составляем таблицу 4 для всех возможных комбинаций и .

Таблица 4.

.

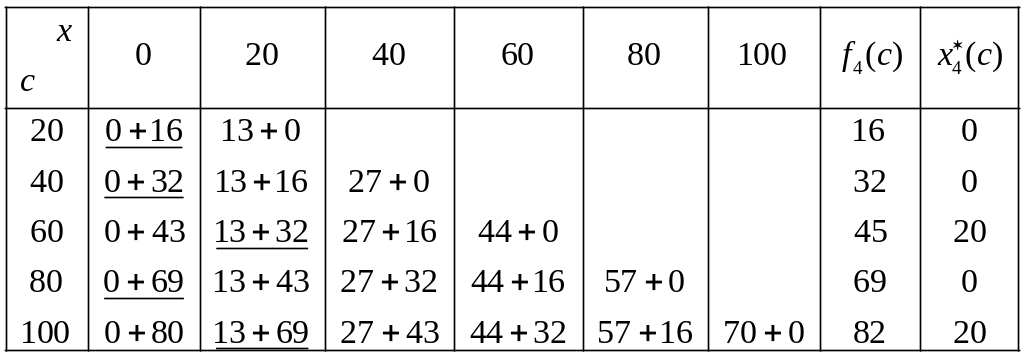В каждую клетку записывается сумма , где первое слагаемое берется из условия, а второе – из таблицы 3. В двух последних столбцах проставлены максимальный по строке прирост продукции и соответствующая сумма средств, выделяемая второму цеху .

Составляем сводную таблицу 5 из последних двух столбцов расчетных таблиц.

Таблица 5.

.

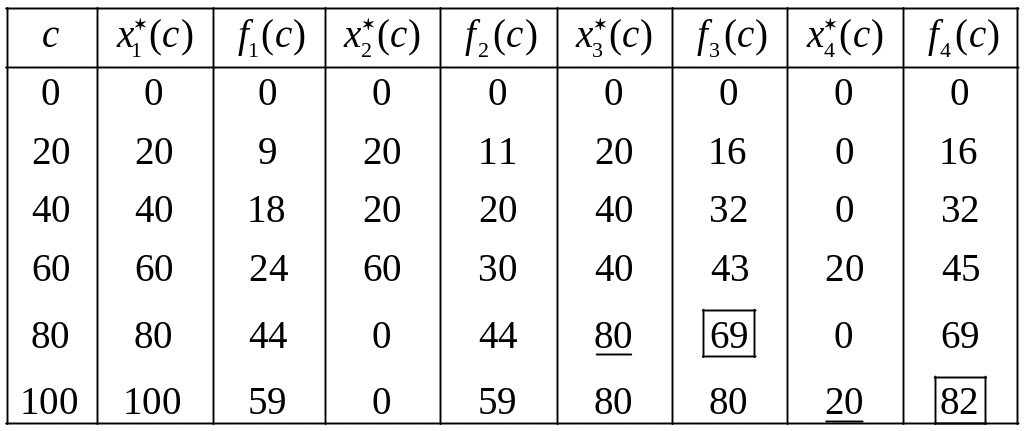Итак, максимальный прирост выпуска продукции в четырех цехах предприятия при распределении между ними 100 тыс. дол. составляет 82 тыс. дол. и будет получен, если первому и второму цехам средства не выделять, третьему цеху выделить 80 тыс. дол., а четвертому – 20 тыс. дол.

Ответ: максимальный прирост составляет 82 тыс. дол.; средства распределяются следующим образом: третьему цеху выделить 80 тыс. дол., четвертому – 20 тыс. дол., первому и второму цехам средств не выделять.

