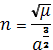2.3 Уравнение Бине

Другой способ получения траектории движения в задаче двух тел связан с широко известным уравнением Бине. Это уравнение записывается в цилиндрической системе координат M0rϕζ, получающейся из рассмотренной ранее системы M0rvζ путем поворота вокруг оси M0ζ на некоторый угол ω∗ согласно равенству:

. (1.36)

Это означает, что направление полярной оси в плоскости ζ=0 в системе M0rϕζ выбирается произвольным, в то время как в системе M0rvζ полярная ось всегда направлена на перицентр орбиты.

Используя обозначения

(1.37)

и известные из теоретической механики проекции ускорения на радиальное, трансверсальное и бинормальное направления

, (1.38)

можно записать дифференциальные уравнения относительного движения тела M в скалярной форме

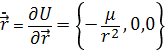(1.39)

. (1.40)

Из второго уравнения (1.41) получаем интеграл площадей в виде

. (1.41)

Подставляя из этого уравнения в первое уравнение (1.41) и делая замену переменных по формулам

………………(1.42)

Уравнение Бине является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Его общее решение имеет вид

, (1.43)

где C1 и C2 - произвольные постоянные интегрирования.

Вместо постоянных C1 и C2 можно ввести величины e и ω∗ по формулам

(1.44)

и с учетом зависимости p = c2/µ записать общее решение в виде

(1.45)

Учитывая (1.36), отсюда получим уравнение орбиты в уже известной форме фокального уравнения конического сечения

, (1.46)

где v = − ω∗ - истинная аномалия.

Глава 3. Типы невозмущенного движения

Результаты проведенного интегрирования позволяют сформулировать два первых обобщенных закона Кеплера. Первый закон: невозмущенной орбитой является кривая второго порядка, в одном из фокусов которой расположено притягивающее тело. Второй закон: площадь, ометаемая радиусом-вектором движущегося тела, изменяется пропорционально времени. Формулировку третьего закона рассмотрим далее для эллиптического движения.

3.1 Определение типа орбиты

Из курса аналитической геометрии известно, что уравнение (1.9) в зависимости от эксцентриситета e и фокального параметра p определяет следующие типы орбит:

p = 0	e = 0,	окружность,
p = 0	0 < e < 1,	эллипс,
p = 0	e = 1,	парабола,
p = 0	1 < e < ∞,	гипербола,
p = 0	e = 1,	прямая.

0

Тип орбиты можно также определить по начальным условиям V0, r0 и начальному углу δ0 между векторами V0 и r0, учитывая, что h = V 2 − 2µ/r0 и c = r0V0 sin δ0:sin δ0 = 1,V0 =,- окружность,r0

sin δ0 = 0,V0 < sin δ0 = 0,V0 = sin δ0 = 0,V0 >2µ,- эллипс,r0

2µ,- парабола,r0;2µ,- гипербола,

r0sin δ0 = 0,V0 − любая,- прямая.

Скорость, определяемая по формуле V=(µ/r), называется первой космической или круговой скоростью.

Такой скоростью обладает тело M при движении по круговой орбите радиуса r. Скорость V=(2µ/r называется второй космической, параболической или скоростью освобождения. Тело, обладающее такой скоростью, при t → ∞ удаляется от центра притяжения на бесконечное расстояние (с нулевой скоростью на бесконечности).

Далее рассмотрим явный вид зависимости истинной аномалии от времени и, в конечном счете, алгоритм расчета координат и компонент скорости как функций времени для каждого типа движения.

3.2 Круговое движение

(p = 0, e = 0)

Круговое движение представляет собой наиболее простой случай движения в задаче двух тел. Только для кругового движения (и прямолинейного движения с нулевой энергией - см. далее) координаты и компоненты скорости движущегося тела выражаются явными функциями времени. Действительно, при движения по круговой орбите радиуса r=p=a орбитальные прямоугольные координаты и компоненты скоростей представляются в виде:

, ,

, , (1.47)

где M = n(t − τ ), n = √µ/a(3/2) - постоянная угловая скорость движения по круговой орбите.

3.3 Эллиптическое движение

(p = 0, 0 < e < 1)

Каноническое уравнение эллипса в прямоугольных координатах Oξ!η! с началом O в центре эллипса и фокальной осью Oξ! имеет вид

, (1.48)

где a - большая, а b - малая полуоси эллипса. Полуфокусное расстояние c = ae связано с полуосями зависимостью

a2 = b2 + c2, откуда b = a,1 − e2, (1.49)

а фокальный параметр орбиты выражается через большую полуось и эксцентриситет формулой

p = a(1 − e2). (1.50)

Вместе с уравнением (1.124) будем рассматривать параметрические уравнения эллипса:

ξ' = a cos E ,η’ = b sin E ,(1.51)

где E - угол с вершиной в центре эллипса, отсчитываемый от оси Oξ! в положительном направлении, т.е. против хода стрелки часов. Этот угол называется эксцентрической аномалией. На рис. 1.4 проведено построение точки M на эллипсе по заданным значениям a,b и E. Уравнения (1.54) предоставляют удобную возможность геометрического построения эллипса по ряду таких точек.

Для получения зависимости между истинной и эксцентрической аномалиями воспользуемся формулами перехода от системы координат Oξ!η! к орбитальной системе M0ξη в плоскости орбиты ζ=0:

ξ=ξ’ − ae,η=η’. (1.52)

Учитывая (1.39), (1.41) и (1.42), получим систему двух уравнений с тремя переменными величинами r, v и E :

Если из этих уравнений исключить эксцентрическую аномалию, то получим уравнение конического сечения (1.66). Исключая истинную аномалию путем возведения уравнений (1.129) в квадрат и последующего сложения, получим зависимость полярного радиуса r и величин r ± r cos v от эксцентрической аномалии E в виде

, (1.53)

(1.54)

Выражения для (r + ξ) и (r − ξ) с учетом (1.129) и (1.130) имеют вид

,

, (1.55)

или, переходя к половинным углам и извлекая квадратный корень, приходим к равенствам:

(1.56)

Отсюда, делением второго соотношения в на первое получим искомую связь истинной аномалии с эксцентрической:

.(1.57)

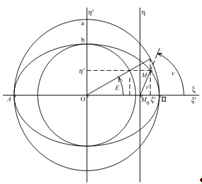
Рис. 1.4. Построение точки эллипса M=(ξ!,η!)=(a cos E,b sin E) по значению эксцентрической аномалии E.

Штриховые прямые, параллельные осям координат, иллюстрируют построение точки M для заданного значения эксцентрической аномалии E . Точка П - перицентр орбиты, А - апоцентр.

Для вычисления интеграла J в его левой части сделаем замену переменной интегрирования.Подставляем выражения

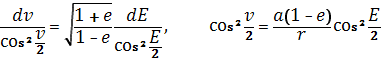
(1.58)

и учитываем, что E = 0 при v = 0, для интеграла J получим

(1.59)

После интегрирования получим окончательное уравнение в виде:

, (1.60)

где введены обозначения

(1.61)

Уравнение называется уравнением Кеплера, величина M в астрономии называется средней аномалией, а величина n - средним движением.

Среднее движение n есть средняя угловая скорость движения по эллипсу. При движении тела по эллиптической орбите истинная, эксцентрическая и средняя аномалии изменяются так, что половины этих углов всегда находятся в одной четверти. Таким образом, эксцентрическую аномалию E можно рассматривать как обратную функцию средней аномалии M =M (E ).

По заданному значению эксцентрической аномалии E средняя аномалия M , а вместе с ней и время t, определяются непосредственно из уравнения Кеплера. Но для вычисления траектории движения по заданным кеплеровским элементам необходимо решить уравнение в обратном направлении: определить E для заданного момента времени t, т.е. приходится иметь дело с трансцендентным уравнением, решить которое в конечном виде невозможно. Для решения уравнения Кеплера можно воспользоваться известными численными методами решения нелинейных уравнений.

Рассмотрим классическую схему метода итераций. В качестве нулевого приближения возьмем E0=M. Тогда первое, второе и последующие приближения получим по формулам:

(1.62)

Ввиду тождественного выполнения условия

(1.63)

итерационный процесс всегда сходится к истинному значению эксцентрической аномалии E . При этом чем меньше эксцентриситет, тем быстрее сходимость итерационного процесса.

Линейные размеры и форму эллиптической орбиты определяют большая полуось a и эксцентриситет e.

Постоянную энергии в эллиптическом движении можно выразить через большую полуось орбиты с помощью формул (1.49) и (1.65):

, (1.64)

где учтено, что c2/µ=p и λ/µ=e.

Период обращения по орбите определяется равенством

(1.65)

Отсюда получается третий обобщенный закон Кеплера в виде

(1.66)

В отличие от формулировки закона, данной Кеплером (T 2/T 2= a3/a3), в левой части уравнения присутствует в качестве множителя сумма масс. Третий закон планетных движений в оригинальной формулировке И.Кеплера можно получить из задачи Кеплера (1.31), для которой m<m0, так что µ=f m0, в то время как в относительном движении µ = f (m0 + m).

С помощью обобщенного закона Кеплера можно определять массы планет, обладающих спутниками. Пусть m0 - масса Солнца, mp - масса планеты, ms - масса спутника планеты, причем m0>mp>ms.

или

(1.67)

где Tp и Ts - периоды обращения планеты и спутника по своим орбитам. С помощью этой формулы можно определить отношение массы планеты к массе Солнца, так как большие полуоси и периоды обращения планеты и спутника весьма точно определяются из наблюдений.

Таблица 1.1. Таблица некоторых кеплеровских элементов

p	e	i

Наряду с введенными ранее кеплеровскими элементами орбиты для эллиптического движения используются также другие элементы, например, представленные в таблице 1.1.

В этой таблице введены некоторые новые элементы: ϕ - угол эксцентриситета, π - долгота перицентра (измеряется двумя углами, расположенными в разных плоскостях), M0 - средняя аномалия в эпоху t0, ε - средняя долгота в эпоху t0, Ω + 180◦ - долгота нисходящего узла орбиты.

В заключение запишем алгоритм вычисления координат и скоростей в эллиптическом движении на заданный момент времени t при известных кеплеровских элементах орбиты a,e,i,Ω,ω и средней аномалии M0 в эпоху t0. Алгоритм задается нижеследующей сводкой формул:

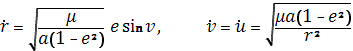
В этом алгоритме направляющие косинусы α, β , γ , α!, β!, γ! зависят от времени, так как функцией времени является аргумент широты u. Для вычисления координат и скоростей можно применить другой алгоритм, в котором используются не зависящие от времени направляющие косинусы орбитальной фокальной системы координат. Сводка формул алгоритма:
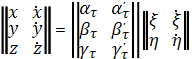