3.1.2 Скорость и ускорение точки

1 При векторном способе задания движения скорость – вектор, направленный по касательной к траектории в сторону движения точки и приложенный в этой точке, который равен первой производной радиус-вектора по времени:

(3.7)

Ускорение – вектор, направленный в вогнутую сторону траектории, равный первой производной по времени от вектора скорости или второй производной по времени от радиус-вектора точки:

(3.8)

2 При координатном способе задания движения, когда, в частности, декартовые координаты x, y, z – известные функции времени, сначала определяются проекции скорости на соответствующие декартовые оси

(3.9)

затем – модуль и направляющие косинусы вектора скорости

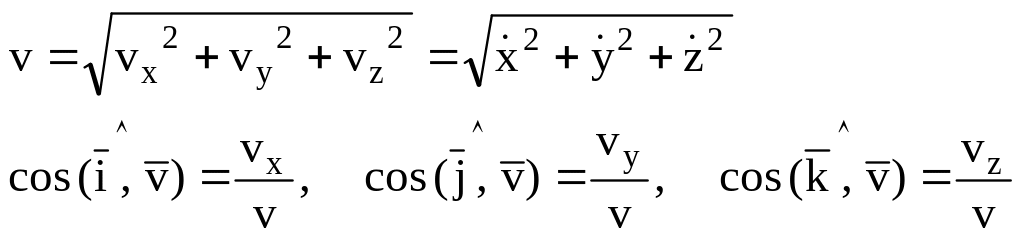(3.10)

Декартовые проекции, модуль и направляющие конусы вектора ускорения определяются по формулам:

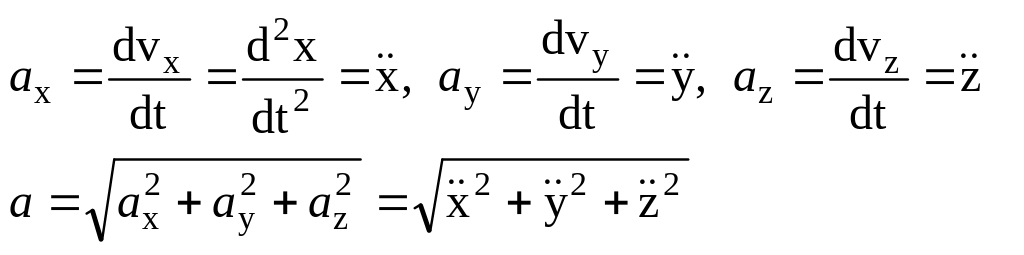(3.11)

(3.12)

3 При естественном способе задания движения скорость и ускорение определяются по их проекциям на естественные оси, начало которых находится в движущейся точке, а – направляющие орты (рис. 3.5). При этом скорость точки определяется как алгебраическая величина

(3.13)

Скорость точки как векторную величину можно представить в виде

(3.14)

Ускорение определяется про формулам:

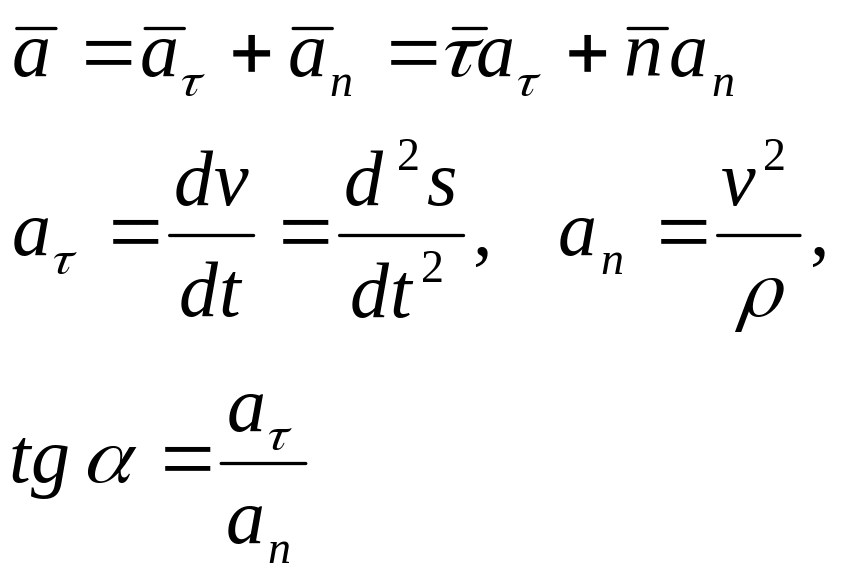
(3.15)

Рис. 3.5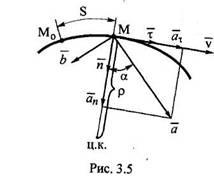

Здесь – единичный вектор касательной, – единичный вектор главной нормали, – единичный вектор бинормали, – соответственно касательное и нормальное составляющие полного ускорения, причем ,  – радиус кривизны траектории для т. M,  – направляющий угол полного ускорения. Таким образом, движение точки исследуется в подвижной ортогональной системе координат, начало которых находится в самой движущейся т. M, а их направления определяются ортами В силу такого выбора системы координат третьей составляющей ускорения не будет, т.е. ¹. В этом заключается существенное отличие естественного способа задания движения точки от задания её движения в декартовой системе координат. Естественный способ задания движения часто используется при исследовании криволинейного движения точки и особенно – движений точек вращающихся тел.

3.1.3 Частные случаи движения точки

1 Равномерное прямолинейное движение. При этом а = 0 (а_ = 0, а_n = 0,  = ), v = const и закон движения определяется по формуле:

S = S_o + vt (3.16)

где S_o = S(0).

2 Равномерное криволинейное движение. При этом а = а_n, a_ = 0, v = const, уравнение движения описывается выражением (3.16).

3 Равномерное движение по окружности. При этом а = а_n = const, a_ = 0, v = const. Отсюда следует, что  = const. Траекторией движения точки является дуга окружности, так как радиус кривизны только окружности есть  = R = const (R – радиус окружности). Закон движения имеет также вид (3.16).

4 Переменное прямолинейное движение. При этом а = а_, а_n= 0, так как  = . Тогда

(3.17)

5 Переменное криволинейное движение. В этом случае

(3.18)

В выражениях (3.17) и (3.18) знак (+) принимается в случае равноускоренного движения, знак (–) – равнозамедленного движения точки.