8.2.2. Получение цифровой голограммы Фурье и ее бинаризация

Рассмотрим более подробно процедуру получения цифровой голограммы. Сделаем это на примере голограммы Фурье, принцип регистрации которой был рассмотрен в параграфе 3.5.2. Как и всякие другие цифровые модели, цифровые модели голограмм воспроизводят процесс лишь приближенно, однако наиболее существенные свойства, подлежащие исследованию, представляются четко выделенными, в явном виде, что часто нельзя сделать в реальном процессе. Одно из основных приближений связано с переходом от непрерывных величин к дискретным, с которыми работает ЭВМ. Этот переход, уменьшая точность результатов, в то же время не вносит принципиальных изменений в процесс, так как с уменьшением шага дискретизации модель все более приближается к непрерывной. Степень такого приближения ограничена лишь возможностями ЭВМ. Кроме того, есть разумный предел плотности дискретизации, определяемый разрешающей способностью оптических элементов и фотоматериалов, участвующих в голографическом процессе. Этот предел для функций с ограниченным спектром определяется известной специалистам теоремой Котельникова, из которой следует, что если функция имеет спектр, ограниченный частотой f0, то она может быть представлена с большой точностью в точках xm, отстоящих одна от другой на расстоянии . Теорема Котельникова легко распространяется на двумерные функции. В этом случае отсчеты берут в узлах прямоугольной сетки с размерами ячеек.

И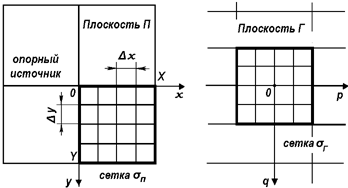 так, переходя к цифровому моделированию голографического процесса, заменим части плоскостей П и Г (см. рис. 3.5.2), ограниченные прямоугольными апертурами, сетками. В узлах этих сеток зададим отсчеты поля. Эти сетки в плоскости предметов обозначим П, а в плоскости голограммы -  Г . Для удобства последующих преобразований расположение сеток в плоскостях П и Г выберем таким, как показано на рис. 8.2.1.

Рис. 8.2.1 Расположение сеток

Правомерность такого выбора будет видна из дальнейшего. Чтобы параметры сеток отвечали теореме Котельникова, необходимо выполнение следующих соотношений:

(8.2.1)

П ри этом суммарное число узлов сетки  П равно MN. Перейдем в плоскости П к новым координатам. Приняв размеры сетки Х=У=1, получаем:

(8.2.2)

Следовательно, координаты узлов сетки  П выразятся так:

( 8.2.3)

Ч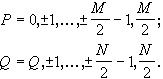 исло узлов сетки  Г выбирают так, чтобы было обеспечено взаимно однозначное соответствие между изображениями, заданными на  П и его дискретным преобразованием Фурье, заданным на  Г. Это число узлов также оказывается равным MN. Последнее определено тем, что в системе, состоящей из MN точек, полной является система тригонометрических функций с частотами

(8.2.4)

Соотношения между размерами сеток _П и _Г получим из (4.2.1) с учетом того, что и согласно (3.5.7)

( 8.2.5)

Выбор сеток в плоскостях П и Г означает, что все непрерывные функции в этих плоскостях могут быть представлены своими дискретными значениями в узлах сетки. Эти значения теперь являются функциями номеров узлов, т.е. m и n в плоскости П, p и q в плоскости Г. Для отличия от непрерывных величин аргументы дискретных величин будем обозначать индексами, например Еmn, вместо Е(хm,уn), Аpq вместо А(р,q). Установим соответствие между основными физическими величинами, рассмотренными ранее, и их цифровыми моделями. Поле в плоскости П представим так:

( 8.2.6)

д искретное преобразование Фурье от hmn определит соотношение:

(8.2.7)

П римем c учетом (4.2.6)

(8.2.8)

Ц ифровая модель голограммы Фурье, являющаяся аналогом ранее рассмотренной модели (3.5.22), будет иметь вид

(8.2.9)

где

( 8.2.10)

Величину можно интерпретировать как коэффициент двойного ряда Фурье от дискретной функции, заданной на двумерном интервале MN. При этом в уравнении голограммы последнее слагаемое является не чем иным, как косинусным коэффициентом Фурье изображения предмета. С учетом изложеного уравнение цифровой голограммы Фурье, удобное для расчетов на ЭВМ, принимает вид:

( 8.2.11)

З десь в общем случае имеем

(8.2.12)

(8.2.13)

( 8.2.14)

В двух первых формулах последние члены в прямоугольных скобках используются при наличии рассеивателя со случайной фазой. Если рассеиватель не используют, то они равны нулю и формула упрощается.

При компьютерном расчете структуры голограммы исходной информацией является изображение, которое разбивают на отдельные участки в соответствии с выбранной сеткой (т.е. из изображения делают выборку значений Еmn в узлах сетки), а также задаваемые параметры M, N, kГ, α,β. В результате расчета должны быть получены величины τ_pq прозрачности голограммы в узлах сетки σ_Г.

Основой вычисления является выполнение дискретного преобразования Фурье (ДПФ), причем двумерное преобразование выполняется в два этапа: сначала по строкам, а затем по столбцам. Последовательность вычислений показана на рис. 8.2.2. Для выполнения одномерных преобразований используется алгоритм быстрого преобразования Фурье (БПФ).

Рис. 8.2.2. Последовательность вычислений голограммы Фурье

В приложении 1 содержится краткое описание процедур ДПФ и БПФ, которые широко вошли в практику компьютерных расчетов. Для удобства вычислений матрицу C_pq , полученную после преобразования строк, транспонируют и повторное преобразование также выполняют по строкам. В результате двойного БПФ получают коэффициенты a_pq и b_pq по которым и определяют значения A_pq². Результаты вычислений вместе с заданными параметрами используют для расчета прозрачности голограммы по ее формуле. Эти значения и выдает машина.

О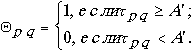 тпечатанную цифровую голограмму затем фотографируют с соответствующим уменьшением и используют для восстановления изображения оптическим путем. Очень часто голограмму Фурье пеставляют в двоичном (бинарном) виде. В этом случае ее прозрачность имеет только два значения: 0 или 1. Двоичную голограмму рассчитывают следующим образом. Прозрачность голограммы как функцию пространственных частот обозначим через Q_pq . Выберем некоторый порог А'. Если τ_pq больше или равно А', то величине Q_pq сопоставим единицу, в противном случае– нуль. Это возможно записать как

(8.2.17)

В данном случае 1 соответствует уровню белого, а 0 - черного.

Окончательно получим

(8.2.18)

В выборе параметров  и A_пор имеется определенный произвол. В общем случае их увеличение приводит к снижению доли высоких пространственных частот в голограмме. Сама же двоичная голограмма в большой степени подчеркивает высокие пространственные частоты.