Чисельне рішення звичайних диференціальних рівнянь

9.1. Необхідні відомості про диференціальні рівняння першого порядку

Задача Коші. Нехай дане звичайне диференціальне рівняння першого порядку виду

(9.1)

у припущенні, що функція f неперервна як функція двох змінних в області свого визначення Df.

Визначення 9.1. Функція 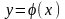, неперервно дифференційована на деякому скінченому або нескінченному проміжку з R і перетворює на ньому рівняння (9.1) в тотожність

(9.2)

вона називається розвязком рівняння (9.1) на цьому проміжку.

Розрізняють загальне розвязання диференціального рівняння, яке записується у вигляді функції

(9.3)

з довільною числовою постійною C, і частковий розв’язок , що виходить із загального рішення при конкретному (допустимому) значенні числового параметра .

Для виділення часткового розвязку зазвичай ставиться умова, якій повинен задовольняти цей розвязок:

при (9.4)

чи,скорочено, 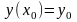. Зрозуміло, що тут .

Співвідношення (9.4) називають початковою умовою, числа та - початковими даними, а точку - початковою точкою.

Визначення 9.2. Завдання знаходження часткового розвязку рівняння (9.1), що задовольняє початковій умові (9.4),називається задачею Коші. Задачу Коші можна вирішити без виявлення загального рішення. Якщо ж загальне рішення (9.3) відомо і початкова умова (9.4) дана, то число , що визначає шуканий частковий розвязок, знаходять з рівняння відносно С:

.

Приклад 9.1. Загальним розвязком диференціального рівняння

на усім R являється функція . При вийде частковий розв’язок

, а число дає часткове рішення .

Нехай необхідно розв’язати задачу Коші з початковою умовою

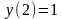. Для цього спочатку знайдемо із рівняння , а потім, підставивши це значення С в загальний розв’язок, отримаємо шуканий частковий розв’язок 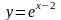. Графік розвязку диференціального рівняння називається інтегральною кривою цього рівняння. Загальний розвязок (9.3) визначає сімейство інтегральних кривих (кожному конкретному значенню С відповідає своя крива), що мають, як правило, однакову або схожу конфігурацію. Наприклад, графіки усіх знайдених в прикладі (9.1) рішень, за винятком прямої , є експоненціальними кривими. Геометричний зміст задачі Коші полягає в знаходженні інтегральної кривої, що проходить через початкову точку . Зокрема, через точку з прикладу (9.1) пройде крива .

Існування і єдиність розвязку задачі Коші. Перш ніж приступати до розв’язку задачі Кошs, заздалегідь потрібно з'ясувати, чи існує розв’язок рівняння, задовольняюче даній початковій умові, а якщо так, то скільки їх може бути. Справедлива наступна теорема.

Теорема 9.1 (теорема Пікара). Нехай точка являється внутрішньою точкою замкнутої прямокутної області

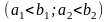, і на області D виконані умови:

1) функція f неперервна як функція двох змінних;

2)часткова похідна існує і обмежена як функція двох змінних (зокрема, неперервна в цій області).

Тоді знайдеться такий відрізок , на

якому рівняння (9.1) має єдине рішення , що задовольняє початковій умові (9.4). Зауважимо, що в якості початкової точки в теоремі Пікара можна взяти будь-яку внутрішню точку області D. Отже, через кожну таку точку в досить малій її околиці проходить єдина інтегральна крива з сімейства . Зрозуміло, що коли f і , неперервні на , задача Коші має єдине рішення при будь-якій початковій точці . Далі займемося пошуком наближень до рішення задачі Коші, вважаючи його єдиним. Приймемо наступну угоду. Угода 9.1. Вважатимемо, що усі подальші міркування і обчислення, пов'язані з наближеним розв’язком задачі Коші, проводяться усередині деякої замкнутої прямокутної області D, де виконуються умови теореми Пікара.

Геометричний зміст правої частини диференціального рівняння (9.1). Візьмемо довільну точку на інтегральній кривій (мал.9.1). Оскільки функція φ є розвязком, справедливе співвідношення

(9.5)

З іншого боку, по геометричному змісту похідної, , де - кут між дотичною, проведеною до даної кривої в точці А, і позитивним напрямом осі Ох. Звідси витікає, що , тобто значення функції 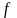дорівнює кутовому коефіцієнту дотичної, проведеної в точці А до інтегральної кривої .

Отриманий результат справедливий для будь-якої внутрішньої точки з області . Обчисливши , отримаємо кутовий коефіцієнт дотичної до деякої,інтегральної кривої,що проходить через цю точку, при цьому сама крива може бути невідома. Можна сказати, що значення визначають напрями інтегральних кривих рівняння (9.1) в тих точках, де вони обчисленні.

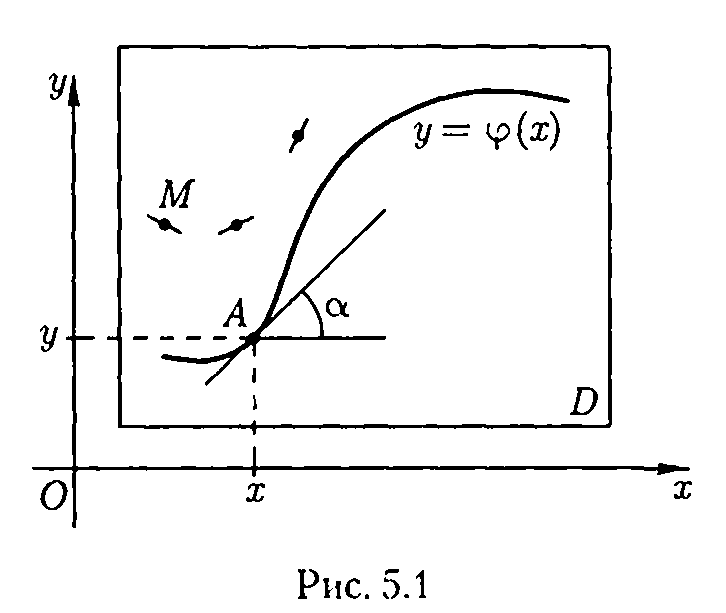
Рис(9.1)

Напрям кривої в точці зазвичай вказується за допомогою відрізку невеликої довжини з центром в М з кутом нахилу до позитивного напряму осі Ох. Провівши досить велике число таких відрізків, отримуємо деяке попереднє уявлення про конфігурацію інтегральних кривих рівняння.

Вправи

9.1. 1. Проілюструйте геометрично отримані в прикладі 9.1 результати.

2. Відмітьте на графіці напрями інтегральних кривих рівняння з прикладу 9.1 в точках 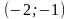та .

9.2. Нехай дане диференціальне рівняння і внутрішня точка області визначення функції f.

1. Переконаєтеся, що функція є рішенням рівняння при усіх .

2. Запишіть в інтегральній формі часткове рішення цього рівняння, що задовольняє початковій умові .

9.3. Дано рівняння . Доведіть, що завдання Коші з початковою умовою має єдине рішення, і знайдіть це рішення двома способами : виділенням параметра С із загального рішення і за допомогою результату з вправи 9.2 (завдання 2).

9.4. Доведіть, що задача Коші для рівняння має єдине рішення при будь-якій початковій точці .

9.5. Дано рівняння . Наведіть приклади замкнутих прямокутних областей А, де виконуються умови теореми Пікара для задачі Коші з початковою умовою .