3.3. Простейшие задачи квантовой механики

Теоретическое введение

3.3.1. Прохождение частиц через потенциальный барьер

Различие в поведении квантовых и классические частиц проявляется в том случае если на пути частицы встречается потенциальный барьер (при , при )

Для классической частицы: если Е – полная энергия частицы меньше U₀ то она не преодолеет и, потеряв часть скорости, будет двигаться вдоль Х.

Для квантовой частицы: если ,она проникнет на некоторую глубину, а затем начнет двигаться обратно.

Г лубиной проникновения . при которой вероятность нахождения частицы уменьшается в е раз

Например, металлическое тело для свободных электронов является потенциальной ямой с U₀, которая выше Е электрона на 1 эВ. Тогда Å.

Поверхность металла является потенциальным барьером, в который электроны проникают на глубину и возвращаются обратно. Следовательно, поверхность металла окружена облаком электронов.

Даже если , то есть вероятность отражения частицы от барьера

.

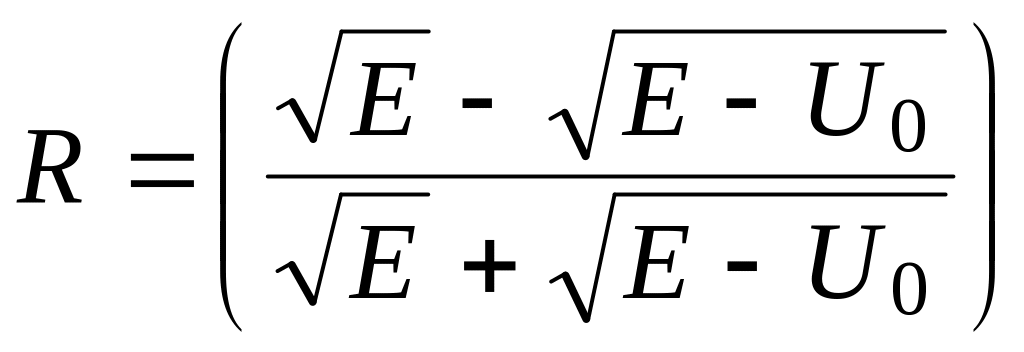Д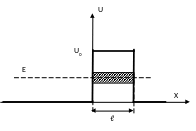 ля барьера конечной ширины вероятность того, что квантовая частица пройдет сквозь него называется коэффициентом прохождения (прозрачности)

Для барьера произвольной формы

Ч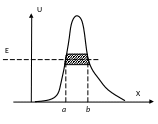 астица как бы проходит через «туннель» в потенциальном барьере и поэтому такое явление называется туннельным эффектом.

В туннеле получается, что кинетическая энергия отрицательна. Такого быть не может, так как одновременно знать кинетическую и потенциальную энергию в квантовой механике невозможно, то же самое, что одновременно и x, следовательно, понятие отрицательной кинетической энергии абсурдно.

3.3.2. Движение частиц в одномерной яме с абсолютно непроницаемыми стенками

В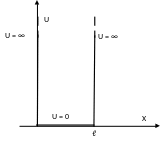 уравнение Шредингера полная энергия Е частицы входит в качестве параметра. В теории дифференциальных уравнений доказывается, что уравнения Шредингера удовлетворят стандартным условиям не при любых значениях Е, а лишь при определенных значениях, которые называются собственными значениями энергии. Решения соответствующие собственным значениям энергии называются собственными функциями. Совокупность собственных значений называется спектром. Спектр бывает дискретным и непрерывным. В случае дискретного спектра собственные значения и собственные функции можно пронумеровать

.

Пусть частица находится между двумя бесконечными стенками, удовлетворяющими условиям

, .

Для одномерного случая уравнение Шредингера

За пределами ямы вероятность обнаружения частицы равна нулю. Следовательно, и . Из условий непрерывности на границах

Для частицы в яме уравнение Шредингера имеет вид

Обозначим . Для уравнения общим решением является

Из условия

Из условия

При то есть частица отсутствует.

Откуда .

Выразив из энергию, получим:

,

С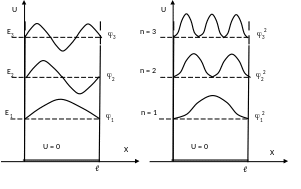 пектр энергии является дискретным. Если вычислитьь разницу между соседними уровнями энергии и в качестве частицы взять молекулу с кг, то для ширины ямы ℓ = 10 см получим эВ. То есть, чем больше m и больше ℓ, тем гуще уровни энергии. Для электрона ℓ ~ 10^-10 м (атомные размеры) эВ.

Найдем собственные функции

Для нахождения А воспользуемся условием нормировки

Функция на концах промежутка х = 0 и x = ℓ обращается в ноль, поэтому интеграл можно получить, умножив среднее значение на ℓ.

Откуда

В состоянии n = 2 вероятность нахождения частицы посередине ямы рана 0. В классической физике все положения частицы равновероятны.

Пример 1. Волновая функция описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной . Вычислить вероятность нахождения частицы в малом интервале  = 0,01 в двух случаях: 1) вблизи стенки (0 < x < );

2) в средней части ящика (( - )/2 ≤ x ≤( + l)/2).

1)0,02; 2)0,01; 3)0,60; 4)0,54.

Решение. Вероятность того, что частица будет обнаружена в интервале dx (от x до x + dx), пропорциональна этому интервалу и квадрату модуля волновой функции, описывающей данное состояние, равна d = (x)²dx.

В первом случае искомая вероятность найдётся интегрированием в пределах от 0 до 0,01:



Так как x изменяется в интервале 0 ≤x ≤0,01 и, следовательно, x/ <, справедливо приближённое равенство

sin²(x/)  (x/)².

С учётом этого выражение (1) примет вид



После интегрирования получим

 = .

Во втором случае можно обойтись без интегрирования, так как квадрат модуля волновой функции вблизи её максимума в заданном малом интервале ( = =0,01) практически не изменяется. Искомая вероятность во втором случае определяется выражением

 = 2(sin²(/2)/ = 20,01/ = 0,02.

Задания к теме

Задание 34

Ч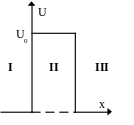 астица массой m с энергией E < U₀ подлетает к потенциальному барьеру высотой U₀ Для области I уравнение Шредингера имеет вид…

*1) ;

2) ;

3) ;

4) .

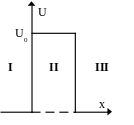З адание 35

Частица массой m с энергией E < U₀ подлетает к потенциальному барьеру высотой U₀ Для области II уравнение Шредингера имеет вид…

*1) ;

2) ;

3) ;

4) .

Задание 36

Н а рисунке приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Состоянию с квантовым числом n = 2 соответствует график …

1); *2); 3); 4).

Задание 37

Н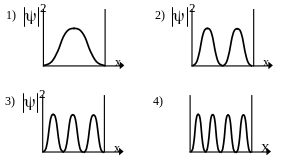 а рисунке приведены картины распределения плотности вероятностей нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Состоянию с квантовым числом n = 4 соответствует график …

1); 2); 3); *4).

Задание 38

В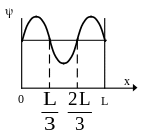 ероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле

,

где ω  плотность вероятности, определяемая ψ- функцией. Если ψ  функция имеет вид указанный на рисунке, то вероятность обнаружить электрон на участке равна …

*1) ; 2) ; 3) ; 4) .

Задание 39

Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле

,

где ω  плотность вероятности, определяемая ψ- функцией. Если ψ  функция имеет вид указанный на рисунке, то вероятность обнаружить электрон на участке равна …

*1) ; 2) ; 3) ; 4) .

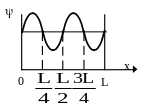З адание 40

Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле , где ω  плотность вероятности, определяемая ψ- функцией. Если ψ  функция имеет вид, указанный на рисунке, то вероятность обнаружить электрон на участке равна …

*1) ; 2) ; 3) ; 4) .

Задание 41

В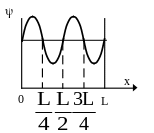 ероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле

,

где ω  плотность вероятности, определяемая ψ- функцией. Если ψ  функция имеет вид указанный на рисунке, то вероятность обнаружить электрон на участке равна …

*1) ; 2) ; 3) ; 5) .

Задание 42

Н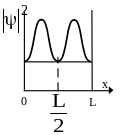 а рисунке изображена плотность вероятности обнаружения микрочастицы на различных расстояниях от «стенок» ямы. Вероятность её обнаружения в центре ямы равна …

*1) 0; 2) ; 3) ; 4) .

Задание 43

Н а рисунке изображена плотность вероятности обнаружения микрочастицы на различных расстояниях от «стенок» ямы. Вероятность её обнаружения на участке равна …

*1) ; 2) ; 3) 0; 4) .

Задание 44

На рисунках схематически представлены графики распределения плотности вероятности обнаружения электрона по ширине одномерного потенциального ящика с бесконечно высокими стенками для состояний с различными значениями главного квантового числа n. В состоянии с n = 4 вероятность обнаружить электрон в интервале от  до l равна

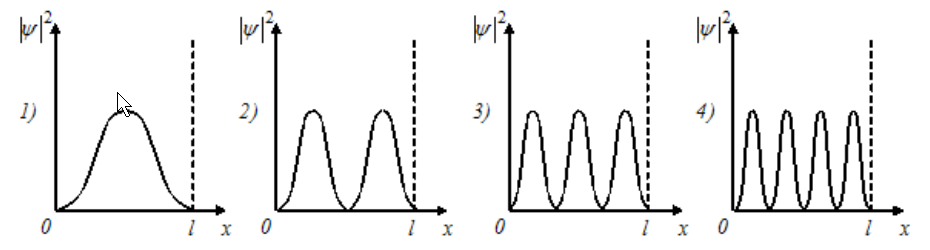
*1) 5/8; 2) 3/8; 3) ¾; 4) 7/8.

З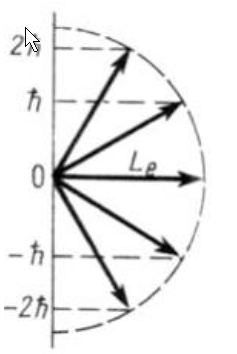 адание 45

На рисунке приведены возможные ориентации вектора – орбитального момента импульса электрона в атоме. Значение орбитального квантового числа для указанного состояния равно:

*1) 2 2) 1 3) 4 4) 5

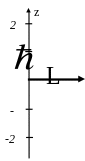
Задание 46

На рисунке приведена одна из возможных ориентаций момента импульса электрона в р-состоянии. Какие еще значения может принимать проекция момента импульса на направление Z внешнего магнитного поля?

1)  2 ^*2)  *3) 4) 2

Задание 47

М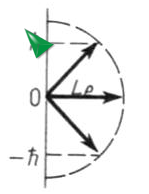 омент импульса электрона в атоме и его пространственные ориентации могут быть условно изображены векторной схемой, на которой длина вектора пропорциональна модулю орбитального момента импульса  электрона. На рисунке приведены возможные ориентации вектора . Значение орбитального квантового числа и минимальное значение главного квантового числа для указанного состояния соответственно равны …

*1) l = 1, n = 2

2) l = 1, n = 1

3) l = 3, n = 3

4) l = 3, n = 4

З адание 48

На рисунке приведены возможные ориентации вектора . Величина орбитального момента импульса (в единицах ħ) для указанного состояния равна …

*1) 2) 3)2 4) 3

З адание 49

На рисунке приведены возможные ориентации вектора . Величина орбитального момента импульса (в единицах ħ) для указанного состояния равна …

1) *2) 3) 2 4) 3

Задание 50

Частица находится в прямоугольном одномерном потенциальном ящике с непроницаемыми стенками шириной 0,2 нм. Если энергия частицы на втором энергетическом уровне равна 37,8 эВ, то на четвертом энергетическом уровне равна _____ эВ.

*1) 151,2 2) 75,6 3) 18,9 4) 9,45