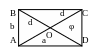
4. Параллелограмм.
Определение. Четырехугольник, у которого противолежащие стороны парами параллелельны, называется параллелограмм.
1. Противолежащие
стороны равны:AB=CD,
BC=AD; диагонали
точкой пересечения делятся пополам:
AO=OC, BO=OD,
противолежащие углы равны:
.
2. Сумма
квадратов диагоналей параллелограмма
равна сумме квадратов всех его четырех
сторон, т.е.
.
C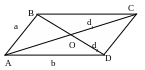
Теорема позволяет:
а) зная две смежные стороны и диагональ параллелограмма найти вторую диагональ;
б) зная две диагонали и одну из сторон найти вторую сторону.
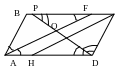
3. Биссектриса AF угла A параллелограмма ABCD отсекает от него равнобедренный треугольник ABF т. е. АВ= АF, биссектриса DP угла D параллелограмма ABCD отсекает от него равнобедренный треугольник DCP т. е. CDВ= PC.
4. Биссектрисы соседних углов параллелограмма перпендикулярны (AF┴DP), а противоположных - параллельны или лежат на одной прямой (AF ║CH) .
5. Биссектрисы четырех углов параллелограмма при пересечении образуют прямоугольник.
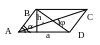
6. Площадь
параллелограмма:
,
S = аbsinα
,
.
5. Ромб.
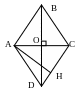
1. Диагонали ромба взаимно перпендикулярны и лежат на биссектрисах его углов.
2. Высоты ромба равны.
3. В любой ромб можно вписать окружность. Ее диаметр равен высоте ромба.
4. Признаки ромба:
а) Если диагонали параллелограмма взаимно перпендикулярны, то это ромб.
б) Если диагональ параллелограмма лежит на биссектрисе его угла, то это ромб.
в) Если стороны четырехугольника равны, то это ромб.
5.
Площадь ромба:
S = ah = a2
sin A =
.
6. Квадрат.
1. У квадрата все углы прямые.
2. Диагонали квадрата равны.
3. Диагонали квадрата пересекаются под прямым углом.
4.
- сторона через радиус описанной
окружности
5.
—
радиус описанной окружности через
сторону
6.
- радиус вписанной окружности
7. Правильный шестиугольник.
1.
—
радиус описанной окружности через
сторону
2.
- радиус вписанной окружности
,
где Р — периметр, а r —
радиус вписанной окружности
3. Сумма
внутренних углов выпуклого n-угольника
равна 1800∙(n-2), где
n— число сторон. Тогда
для правильного n-угольника
угол α :
,
где n— число сторон.
8. Прямоугольник.
1. Диагонали прямоугольника равны.
2. Признаки прямоугольника:
а) Если у параллелограмма диагонали равны, то это прямоугольник.
б) Если у параллелограмма один угол прямой, то это прямоугольник.
в) Если у четырехугольника три угла прямые, то это прямоугольник.
3. Вокруг всякого прямоугольника можно описать окружность. Ее центр лежит в точке пересечения диагоналей.
4. Прямоугольник, у которого диагонали перпендикулярны, это ромб.
5. Прямоугольник, у которого диагональ делит угол пополам, это ромб.
6. Площадь прямоугольника:
S = ab =
d2
sinφ.
9. Трапеция.
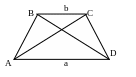
Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны. (ВС║АD— основания, АВ и СD — боковые стороны). Если АВ = СD, то трапеция равнобокая (равнобедренная).
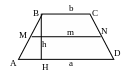
1. Средняя
линия трапеции
.
2. Площадь
трапеции:
,где d1, d2
— диагонали, а φ — угол между диагоналями
.
3. Углы при основаниях и диагонали равнобедренной трапеции равны.
4. Высота
равнобедренной трапеции, опущенная из
вершины большего угла, делит большее
основание на отрезки АН=
и
.
5. Диагонали трапеции делят ее на 4 треугольника: прилежащие к основаниям подобны, прилежащие к боковым сторонам равновелики.
6. Отрезок,
проходящий через точку пересечения
диагоналей параллельно основаниям, с
концами на боковых сторонах равен
.
7. В трапецию можно вписать окружность тогда и только тогда, когда сумма оснований равна сумме боковых сторон, т. е. AD+BC=AB+CD.
8. Только около равнобедренной трапеции можно описать окружность. Ее центр лежит на серединном перпендикуляре к основанию трапеции. Радиус этой окружности равен радиусу окружности описанной около любого треугольника с вершинами в вершинах трапеции.
9. Если центр описанной окружности лежит на основании трапеции, то ее диагональ перпендикулярна боковой стороне.
10. Точка пересечения диагоналей, середины оснований и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой.
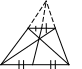
11. Биссектриса угла трапеции отсекает равнобедренный треугольник.
12. Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты: S=h2.
13. Квадрат высоты равнобедренной трапеции, в которую можно вписать окружность, равен произведению оснований: h2=AD∙BC, (AD║BC, AB=CD).