
- •Введение
- •Глава 1. Элементы теории вероятностей
- •§1. Основные правила комбинаторики
- •1. Правило сложения
- •2. Правило умножения
- •3. Размещения
- •Перестановки
- •Сочетания
- •Задачи для самостоятельного решения
- •§2. Классическое определение вероятности
- •Задачи для самостоятельного решения
- •§3. Операции над событиями
- •Задачи для самостоятельного решения
- •§4. Формула полной вероятности. Формула Байеса
- •Задачи для самостоятельного решения
- •§5. Последовательность независимых испытаний (схема Бернулли) Теорема Пуассона. Локальная и интегральная теоремы Муавра – Лапласа
- •Последовательность независимых испытаний (схема Бернулли)
- •2. Локальная теорема Муавра – Лапласа
- •3. Интегральная теорема Муавра – Лапласа
- •4. Теорема Пуассона Если достаточно велико, а - мало, то
- •Решение. Р – мало. Воспользуемся теоремой Пуассона:
- •Задачи для самостоятельного решения
- •§6. Случайные величины. Законы распределения случайных величин. Числовые характеристики
- •Задачи для самостоятельного решения
- •§7. Важнейшие примеры распределений
- •1. Биноминальное распределение
- •2. Нормальный закон распределения
- •3. Распределение Пуассона
- •4. Равномерное распределение вероятностей
- •5. Геометрическое распределение
- •Задачи для самостоятельного решения
- •§8. Системы случайных величин
- •Задачи для самостоятельного решения
§5. Последовательность независимых испытаний (схема Бернулли) Теорема Пуассона. Локальная и интегральная теоремы Муавра – Лапласа
Последовательность независимых испытаний (схема Бернулли)
Испытания называются независимыми относительно события А, если вероятность появления события А в каждом из этих испытаний не зависит от результата, полученного в других испытаниях.
Пусть эксперимент состоит в проведении
независимых испытаний, в каждом из
которых может произойти некоторое
событие А (назовем его “успехом”,
тогда
![]() соответственно “неуспех”). Вероятность
неуспеха равна
соответственно “неуспех”). Вероятность
неуспеха равна
![]() .
В качестве элементарных событий
рассмотрим всевозможные произведения
.
В качестве элементарных событий
рассмотрим всевозможные произведения
![]() (в первом – успех, во втором – неуспех
и т.д.).
(в первом – успех, во втором – неуспех
и т.д.).
Например, если производится 3 испытания
и в них два успеха, то элементарные
события:
![]() ,
,
![]()
![]() .
Вероятности всех этих событий равны:
.
Вероятности всех этих событий равны:
![]() ,
а их число 3. Тогда вероятность события
В (произошло 2 успеха в трёх испытаниях)
равна
,
а их число 3. Тогда вероятность события
В (произошло 2 успеха в трёх испытаниях)
равна
![]() .
.
Рассмотрим общий случай в рамках схемы
Бернулли – нахождение вероятности
того, что в
![]() испытаниях произойдёт ровно
успехов
испытаниях произойдёт ровно
успехов
![]() .
Обозначим эту вероятность
.
Обозначим эту вероятность
![]() .
Событию В (произошло
успехов в
испытаниях) благоприятствуют те
элементарные события, в которые входит
.
Событию В (произошло
успехов в
испытаниях) благоприятствуют те
элементарные события, в которые входит
![]() множителей
множителей
![]() и
и
![]() множителей
;
вероятности событий равны
множителей
;
вероятности событий равны
![]() ,
а их число, как нетрудно видеть, равно
числу способов, сколькими можно выбрать
элементов из
без учёта порядка, т. е.
,
а их число, как нетрудно видеть, равно
числу способов, сколькими можно выбрать
элементов из
без учёта порядка, т. е.
![]() .
Согласно определению вероятности
.
Согласно определению вероятности
![]() ,
(1.12)
,
(1.12)
где . Формулу (1.12) называют формулой Бернулли.
2. Локальная теорема Муавра – Лапласа
Пусть в схеме Бернулли
![]() ,
тогда
,
тогда
![]() при
при
![]() ,
,
где
![]() ;
;
![]() .
Следовательно, при больших
.
Следовательно, при больших
![]() .
(1.13)
.
(1.13)
Для значений функции
![]() составлена таблица (прил. 1).
составлена таблица (прил. 1).
3. Интегральная теорема Муавра – Лапласа
Пусть в схеме Бернулли
- число успехов в
испытаниях и
![]() .
.
Тогда при больших
 ,
,
где
![]() ,
,
![]() .
.
Если обозначить
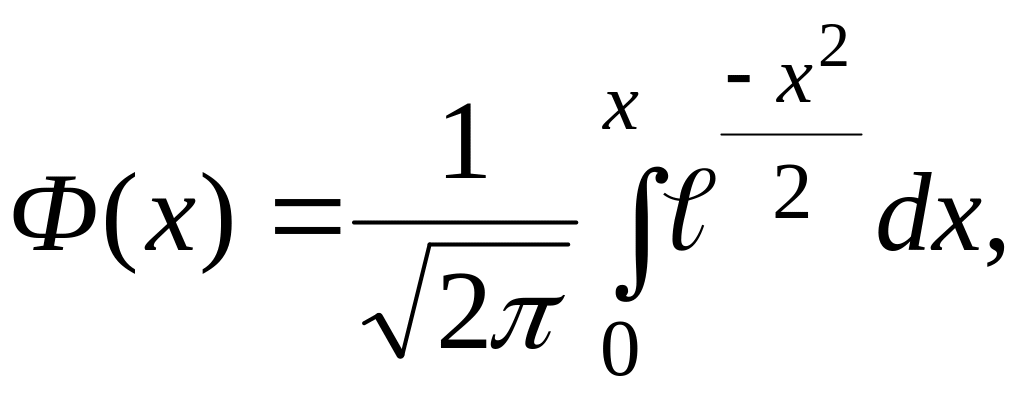 то получаем формулу для вычислений:
то получаем формулу для вычислений:
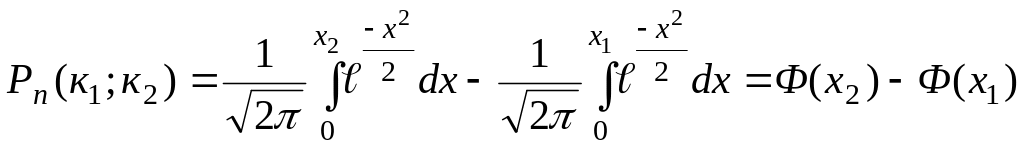 .
(1.14)
.
(1.14)
Для значений функции
![]() ,
соответствующих значениям аргумента
,
соответствующих значениям аргумента
![]() ,
имеется таблица (прил. 2). Для отрицательных
,
имеется таблица (прил. 2). Для отрицательных
![]() значения
можно получить, воспользовавшись
нечётностью
значения
можно получить, воспользовавшись
нечётностью
![]() этой функции, а при
этой функции, а при
![]() можно считать
можно считать
![]() ,
т. к.
,
т. к.
![]() ,
,
![]() и Ф(х) – функция возрастающая.
и Ф(х) – функция возрастающая.
4. Теорема Пуассона Если достаточно велико, а - мало, то
![]() ,
где
,
где
![]() (1.15)
(1.15)
В заключение соберём все результаты
относительно
![]() в следующую схему:
в следующую схему:

Задача 1. В урне 20 шаров: 15 белых и 5 чёрных. Вынули подряд 5 шаров, причём каждый вынутый шар возвращали в урну, и перед извлечением следующего шары в урне тщательно перемешивались. Найти вероятность того, что из пяти вынутых шаров будет два белых.
Решение. Вероятность появления
белого шара в каждом испытании
![]() ,
а вероятность непоявления белого шара
,
а вероятность непоявления белого шара
![]() .
По формуле Бернулли (1.12) находим:
.
По формуле Бернулли (1.12) находим:
![]()
Задача 2. Найти вероятность того, что из 100 независимых выстрелов будет 75 попаданий, если вероятность попадания при одном выстреле равна 0,8.
Решение. Очевидно, мы находимся в рамках схемы Бернулли:
![]() ,
,
![]()
![]() ,
,
![]() .
- достаточно велико, воспользуемся
формулой (1.13):
.
- достаточно велико, воспользуемся
формулой (1.13):
![]()
![]() .
.
По таблице (см. прил. 1) находим:
![]() Тогда
Тогда
![]()
Задача 3. Вероятность появления события при одном опыте равна 0,3. С какой вероятностью можно утверждать, что частота этого события при 100 опытах будет лежать в пределах от 0,2 до 0,4?
Решение. Для того, чтобы частота
лежала в пределах от 0,2 до 0,4 в серии из
100 опытов, число появлений события
![]() должно быть не менее 20 и не более 40
должно быть не менее 20 и не более 40
![]() .
.
Воспользуемся интегральной теоремой Муавра–Лапласа, формулой (1.14).
![]() ,
,
где
,
![]() ,
,
![]() .
.
Следовательно,
![]() ,
,
где значение Ф(2,18) найдено по таблице приложения 2.
![]() .
.
Следовательно,
![]() .
.
Задача 4. Аппаратура содержит 2000 элементов, вероятность отказа каждой из них р = 0,0005. Какова вероятность отказа 3-х элементов, если отказы происходят независимо друг от друга?
