

1. Постановка задачи.
Постановка задачи. Задача о диете состоит в подборке наиболее экономного (дешевого) корма для животных, удовлетворяющего определённым медицинским требованиям.
Имеется n
видов продуктов
питания. Обозначим эти продукты как
![]() ,
Известна стоимость единицы
каждого продукта Сi.
Из этих продуктов необходимо составить
пищевой рацион, который должен содержать
m
видов полезных
элементов (белки, жиры, углеводы и т.п.)
, причем количество каждого элемента в
рационе должно быть не менее Bj.
Обозначим эти компоненты через
,
Известна стоимость единицы
каждого продукта Сi.
Из этих продуктов необходимо составить
пищевой рацион, который должен содержать
m
видов полезных
элементов (белки, жиры, углеводы и т.п.)
, причем количество каждого элемента в
рационе должно быть не менее Bj.
Обозначим эти компоненты через
![]() Для каждой единицы i-го
продукта известно содержание j-го вида
элемента - aij .
Требуется так составить пищевой рацион,
чтобы обеспечить заданные условия при
минимальной стоимости рациона.
Для каждой единицы i-го
продукта известно содержание j-го вида
элемента - aij .
Требуется так составить пищевой рацион,
чтобы обеспечить заданные условия при
минимальной стоимости рациона.
Составим таблицу,
указывающую, какое количество каждого
компонента ![]() содержится в единице веса каждого типа
продуктов
содержится в единице веса каждого типа
продуктов
![]() :
:
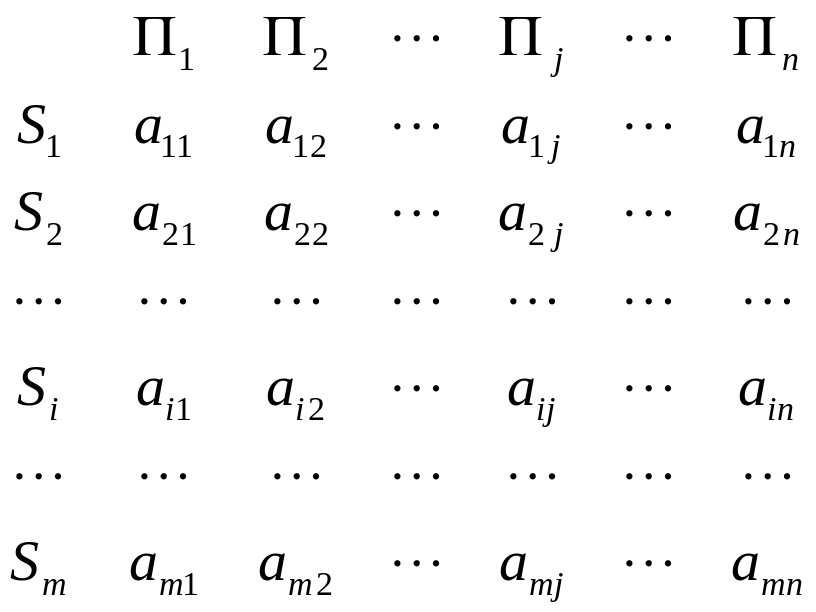
Матрица
![]() называется матрицей питательности.
называется матрицей питательности.
Рацион - это количество единиц
![]() -го
продукта, которое скармливается животному
за определённый срок. К рациону
предъявляются определённые требования:
-го
продукта, которое скармливается животному
за определённый срок. К рациону
предъявляются определённые требования:
должны быть выполнены определённые медицинские требования, которые заключаются в том, что за указанный срок животное должно получить не менее определённого количества единиц каждого компонента. Обозначим через
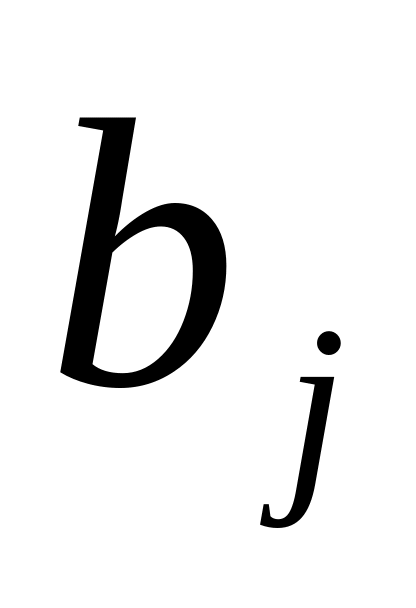 то минимальное количество j-го
компонента, которое должно получить
животное. Тогда рацион должен удовлетворять
ограничениям:
то минимальное количество j-го
компонента, которое должно получить
животное. Тогда рацион должен удовлетворять
ограничениям:
![]() ;
;
2) очевидно что
![]() ;
;
3) стоимость рациона должна быть
минимальной:
![]() ,
,
где z – целевая функция
![]() – цена
компонента
– цена
компонента
4) ограничения на количество объема каждого продукта .
В итоге математическая модель такая, что:
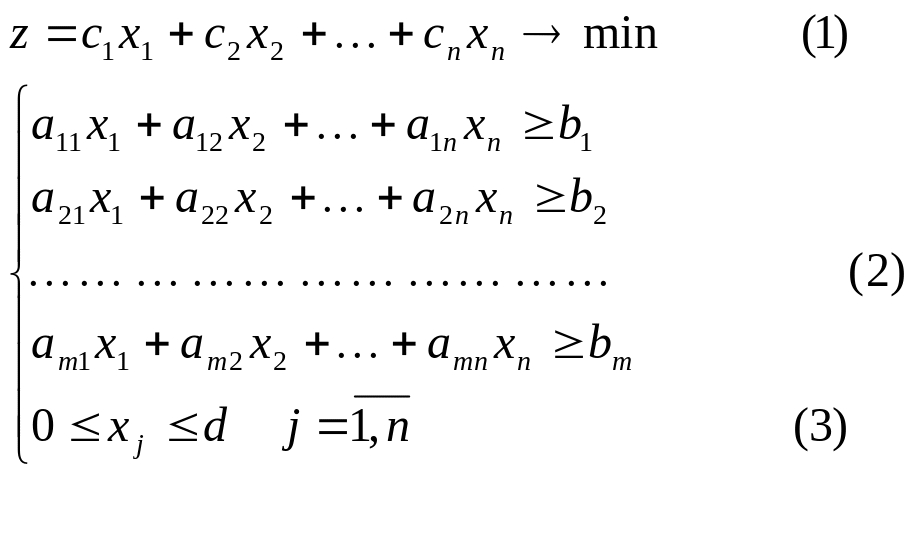
Или в векторной форме:
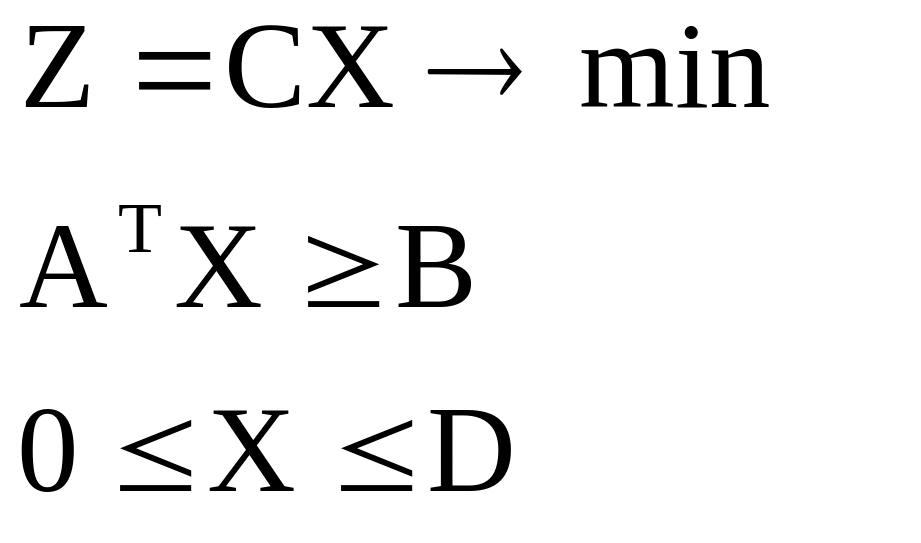
Где
![]() .
.
Так как целевая функция и ограничения являются линейными, то задача решается методами линейного программирования и называется двойственной задачей линейного программирования.
Двойственную задачу можно привести к исходной задаче линейного программирования.

Где
![]()
2. Описание алгоритма
Введем в задачу (4) балансовые переменные
![]() .
Вектор
.
Вектор
![]() называется балансовым вектором, а
переменные - балансовые переменные.
называется балансовым вектором, а
переменные - балансовые переменные.
Тогда система ограничений задачи (4) перепишется так:
![]()
В целевую функцию балансовые переменные входят с нулевыми коэффициентами:
![]()
Или в векторной форме:
![]()
И так вместо задачи (1)-(3) решается задача (5)-(7).
Геометрически система равенств (5)
представляет выпуклый многогранник в
![]() .
В ходе решения симплекс-методом
перебираются пересечения граней этого
многогранника (крайние точки) в направлении
увеличения значения целевой функции.
.
В ходе решения симплекс-методом
перебираются пересечения граней этого
многогранника (крайние точки) в направлении
увеличения значения целевой функции.
В начале считаем, что переменные
![]() - свободные, а
- базисные.
- свободные, а
- базисные.
Введем обозначения:
–
![]() - вектор, составленный из коэффициентов
при переменной
- вектор, составленный из коэффициентов
при переменной
![]() ;
;
–
![]() -
вектор, составленный их коэффициентов
вектора
-
вектор, составленный их коэффициентов
вектора
![]() ,
которые соответствуют текущим базисным
переменным;
,
которые соответствуют текущим базисным
переменным;
–
![]() - симплексные разности для k-ой
крайней точки
- симплексные разности для k-ой
крайней точки
Шаг 1: Для каждой крайней точки строится симплекс-таблица по указанным выше правилам:
-
Базис
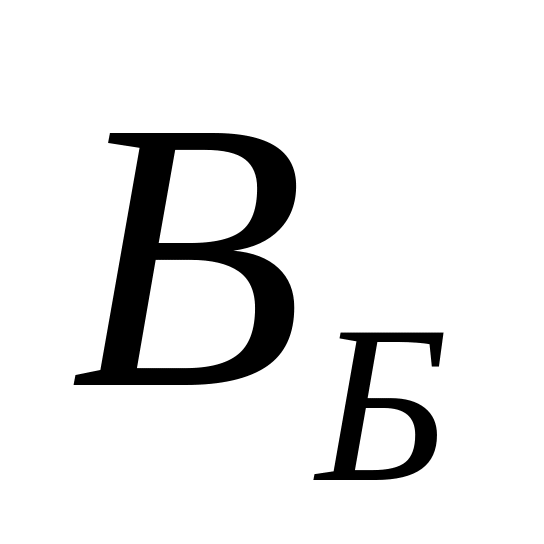
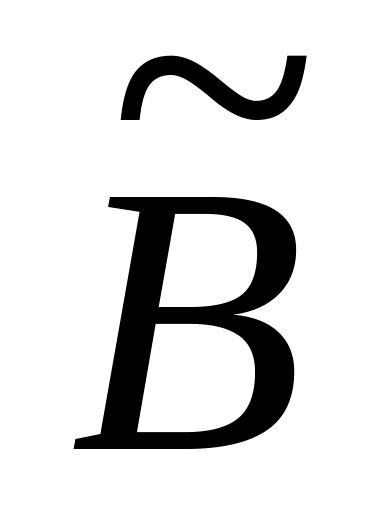
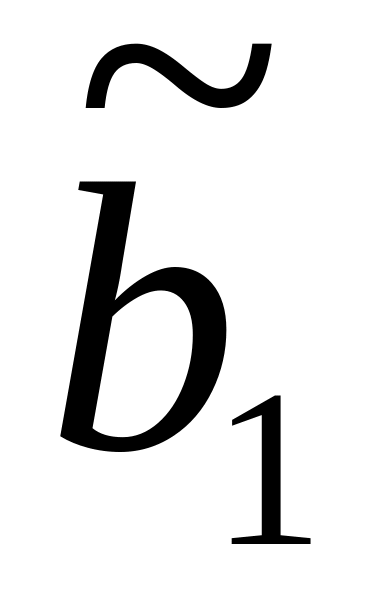
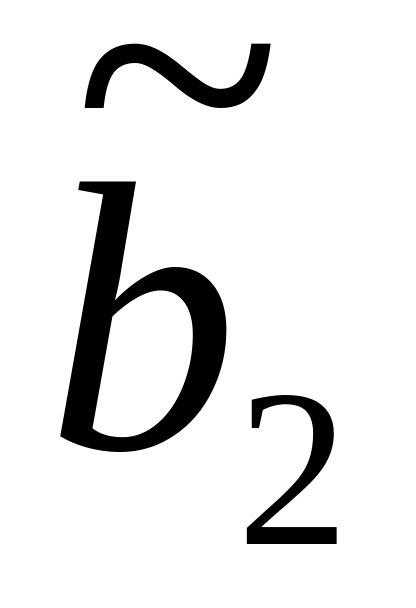
…
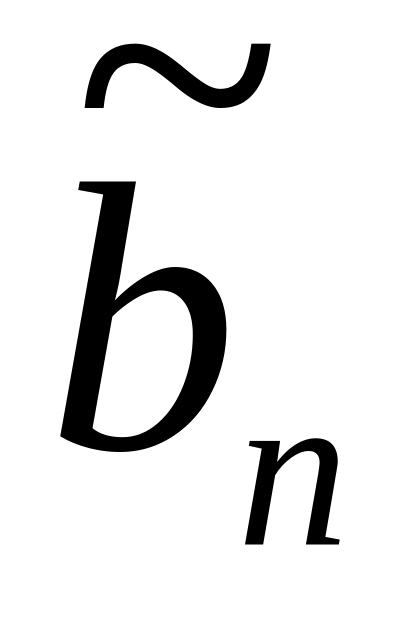
…
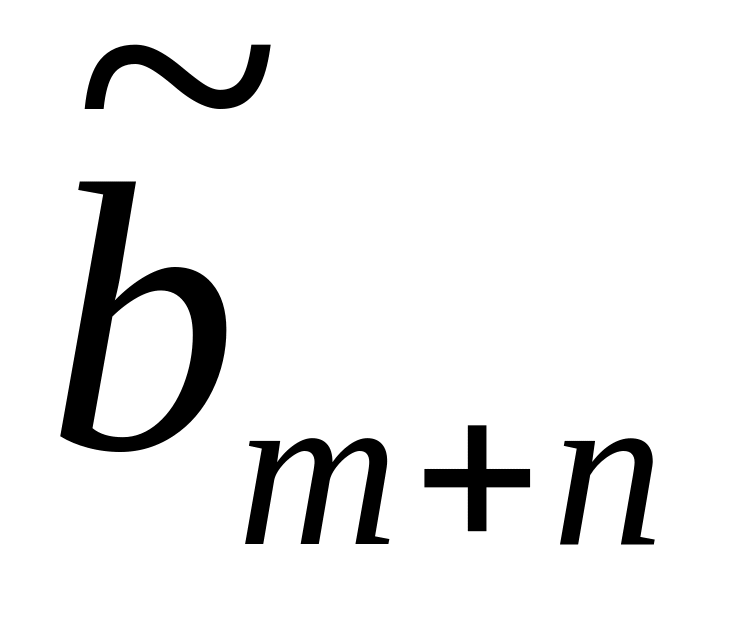
С

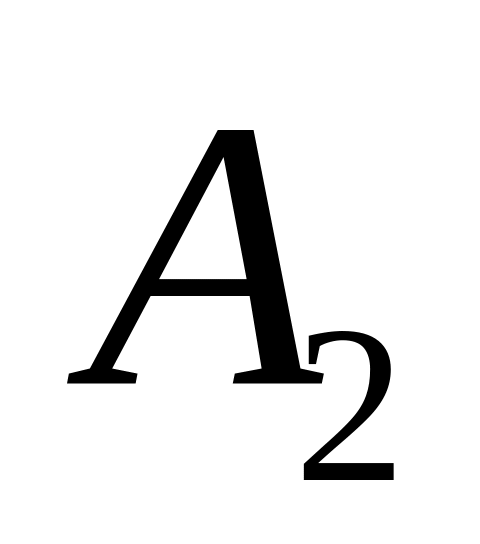
…
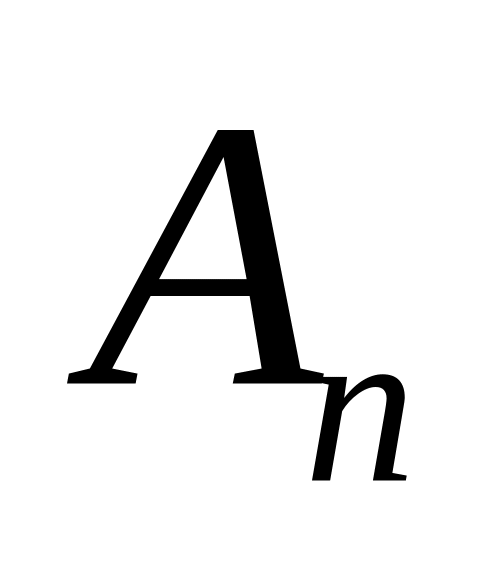
…
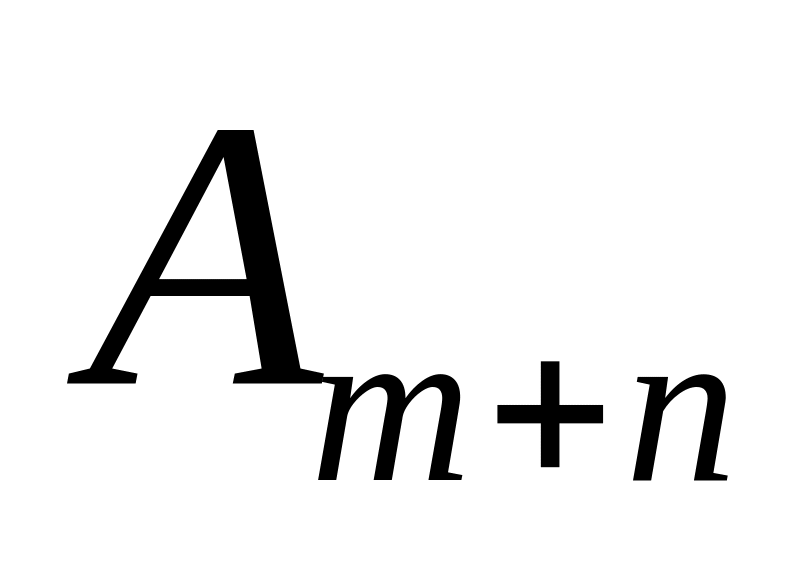
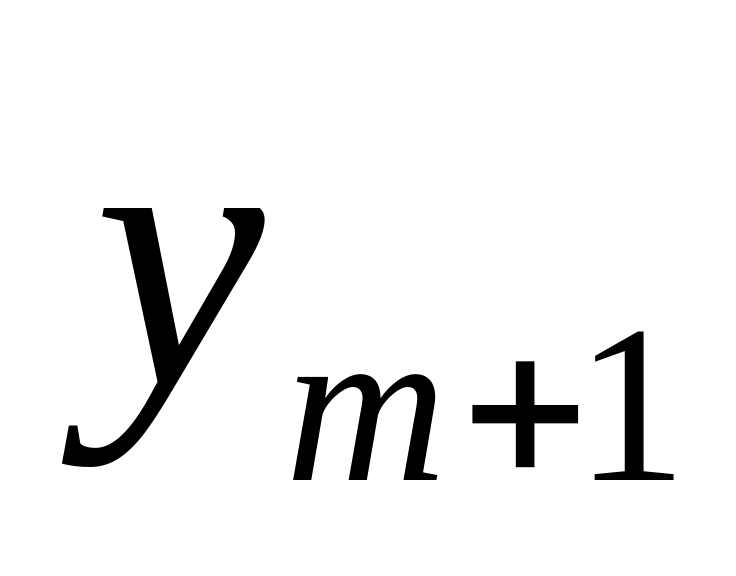

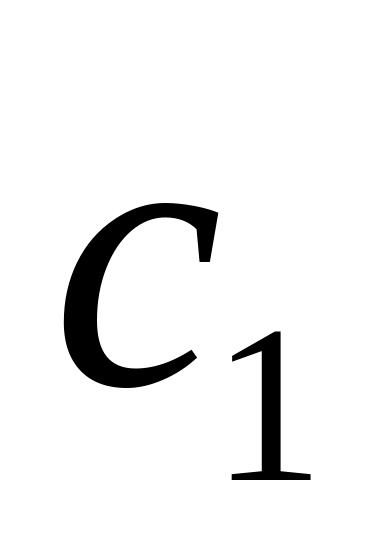

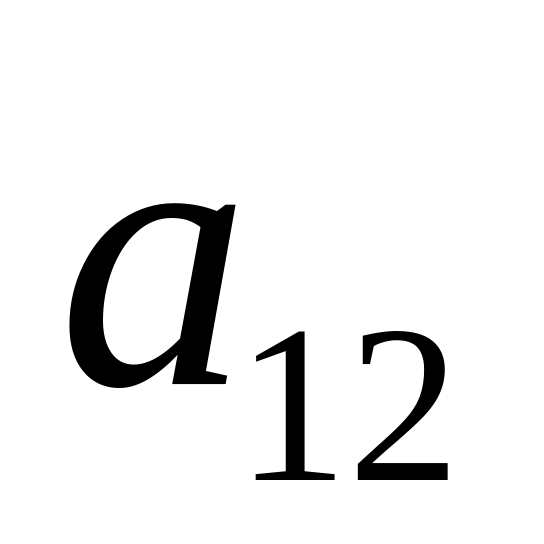
…
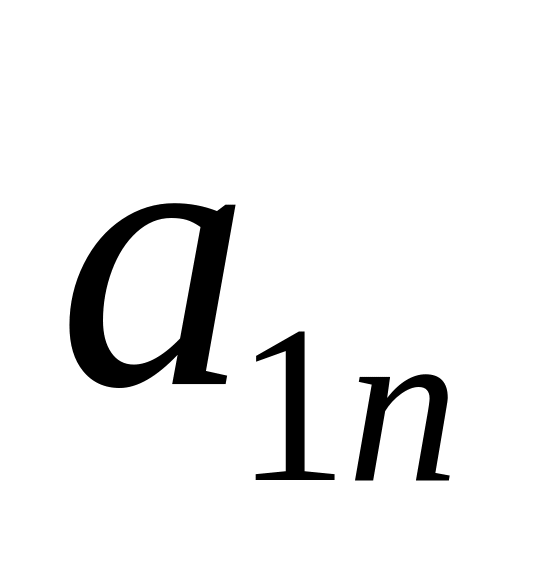
…
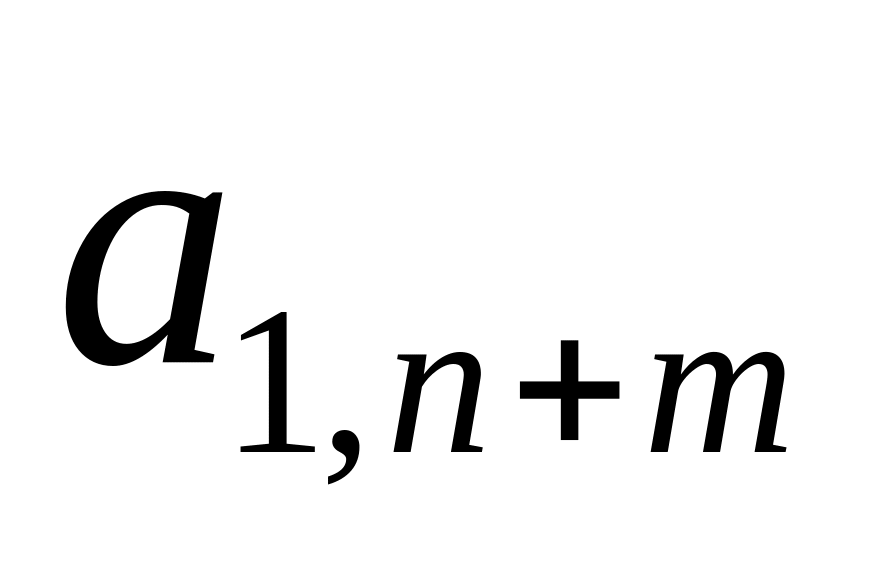
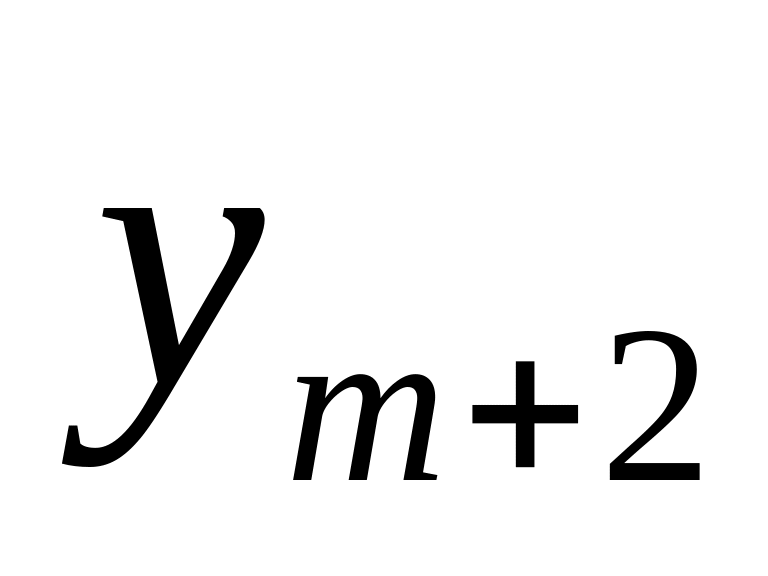
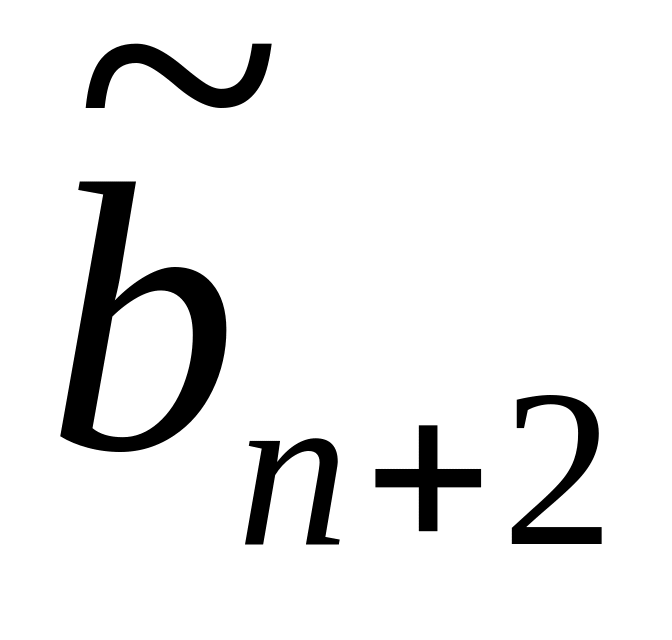
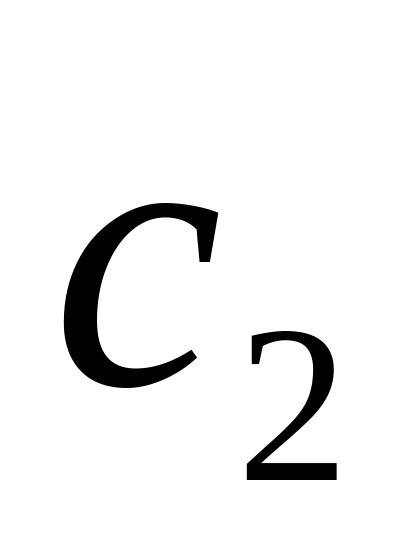
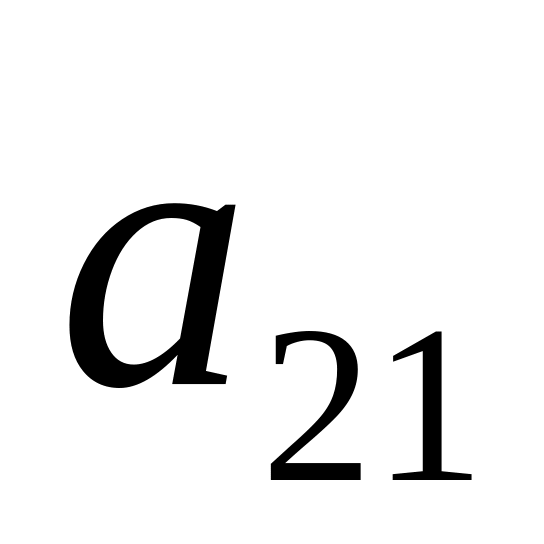
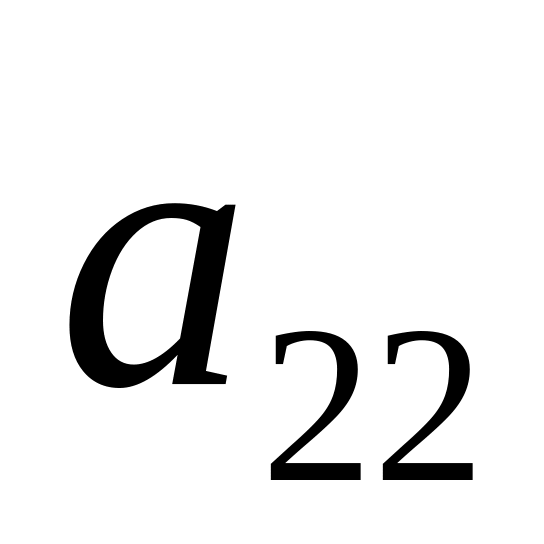
…
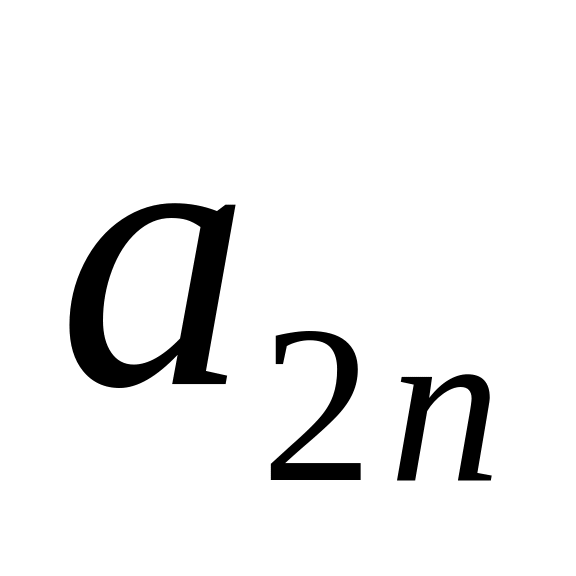
…
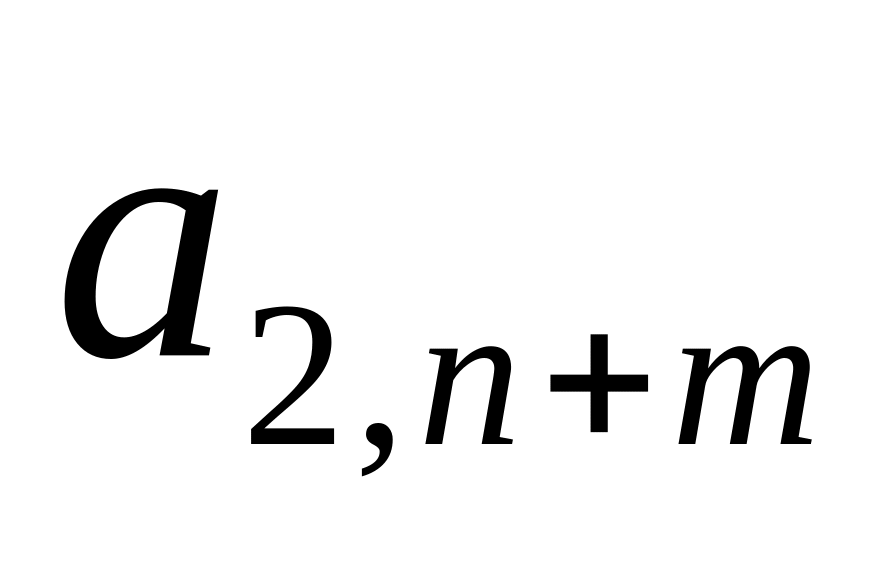
…
…
…
…
…
…
…
…
…
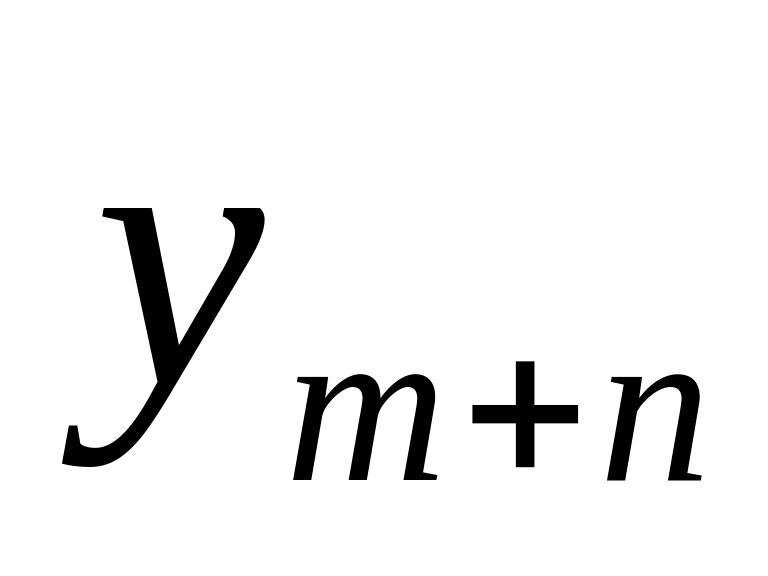
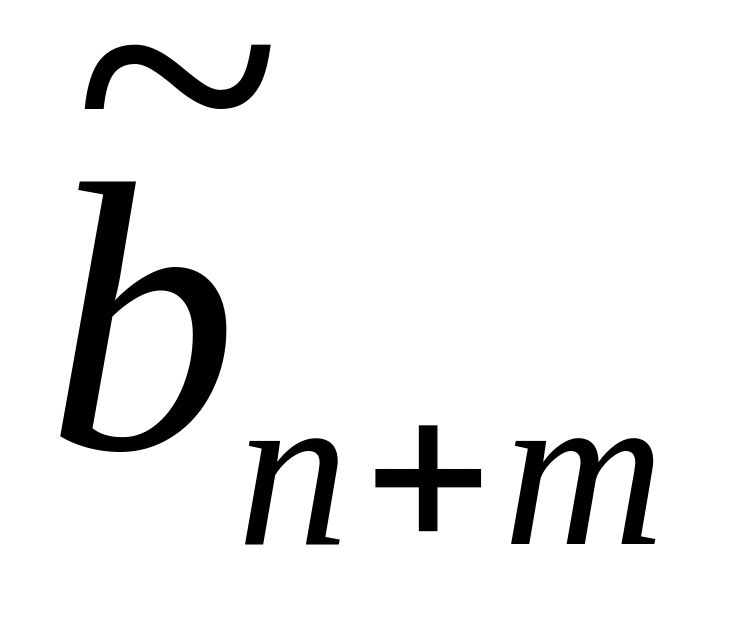
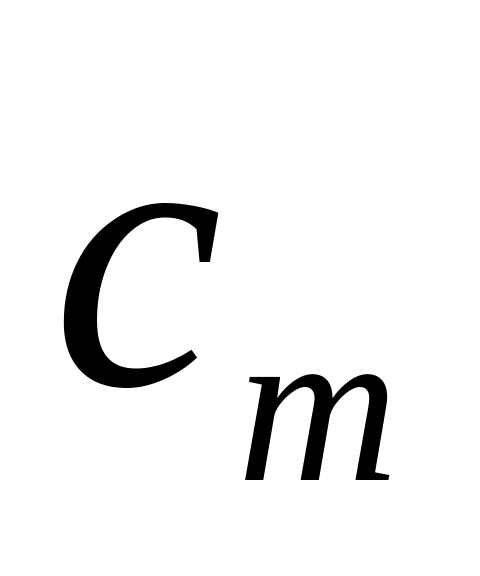
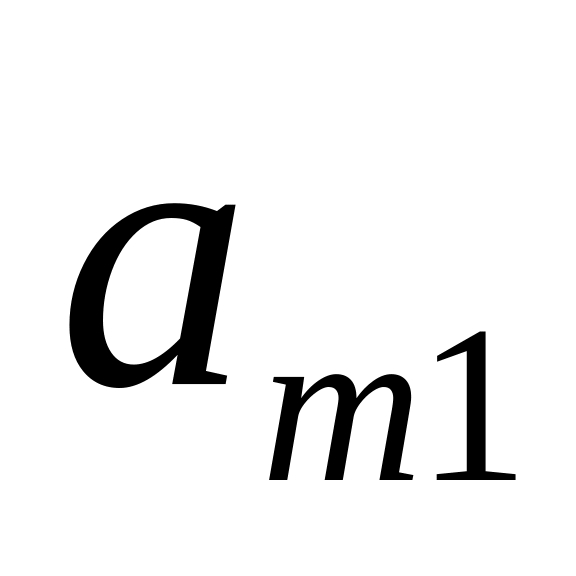
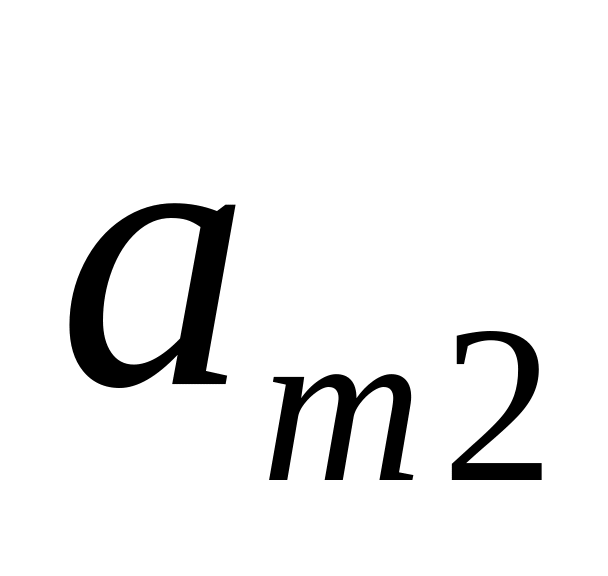
…
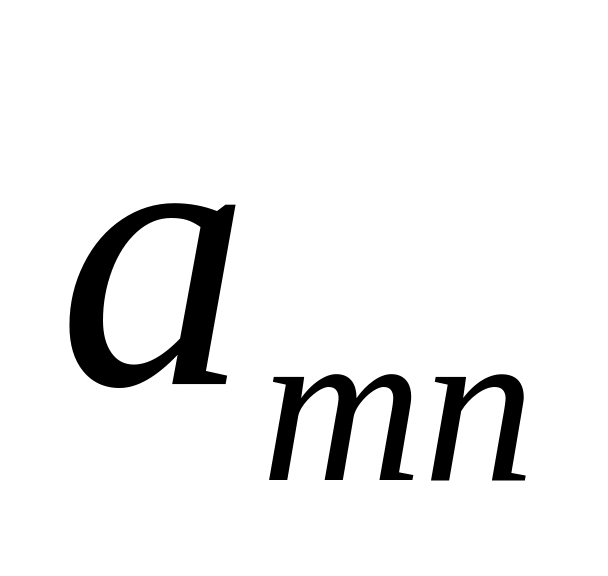
…
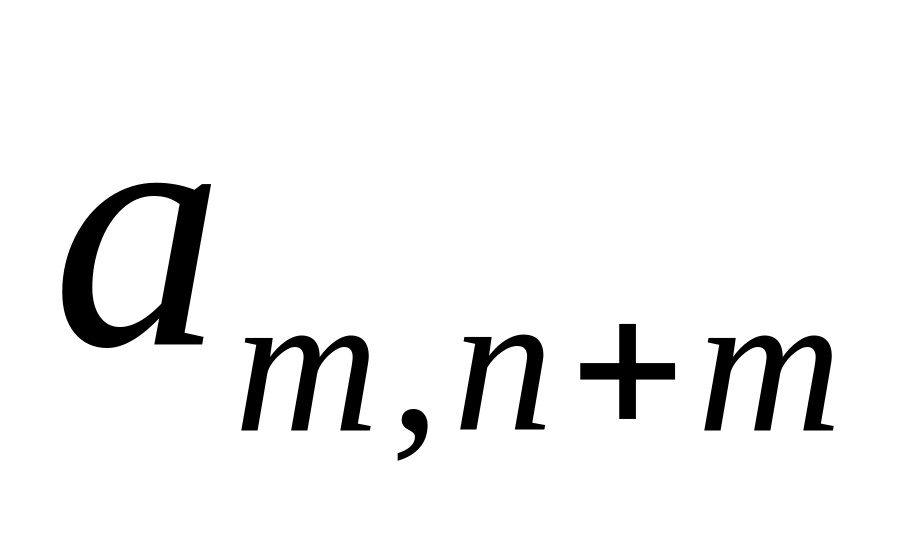
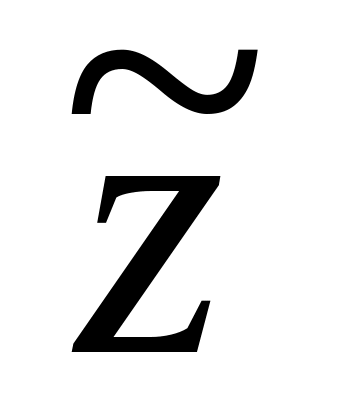

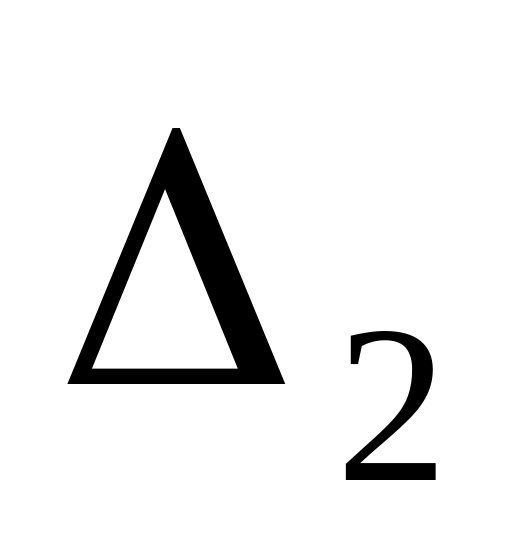
…
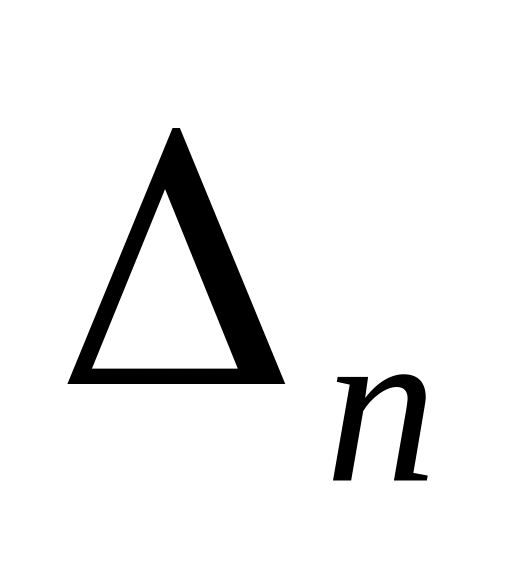
…
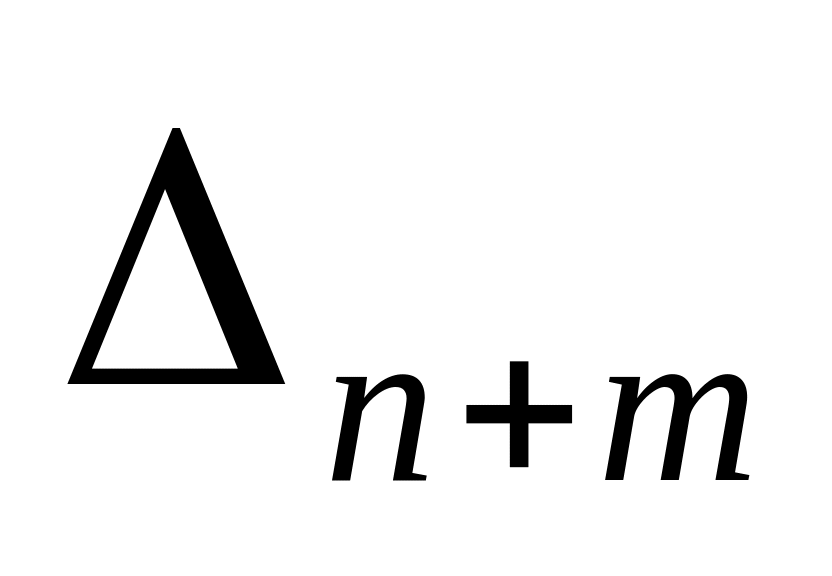
1) Если для k-ой
крайней точки все симплексные разности
![]() ,
то эта точка оптимальна. Конец
решения. Вектор решения
,
то эта точка оптимальна. Конец
решения. Вектор решения
![]() получаем
отбросив балансовые переменные в векторе
получаем
отбросив балансовые переменные в векторе
![]() .
.
2) Если есть столбец, в котором
симплексная разность
![]() ,
а все элементы столбца
,
а все элементы столбца
![]() ,
то задача решения не имеет, т.к.
целевая функция неограниченна сверху.
,
то задача решения не имеет, т.к.
целевая функция неограниченна сверху.
3) В остальных случаях переходим к Шагу 2.
Шаг 2: Находим
![]() -
направляющий столбец. Это такой столбец,
в котором самая минимальная симплексная
разность среди отрицательных разностей:
-
направляющий столбец. Это такой столбец,
в котором самая минимальная симплексная
разность среди отрицательных разностей:
![]() .
.
Находим
![]() - направляющую строку из условия:
- направляющую строку из условия:
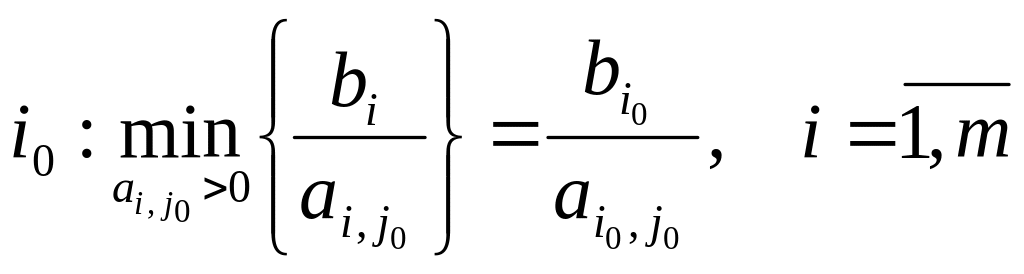 .
.
Тогда направляющий элемент -
![]() .
.
Шаг 3: Теперь вводится новая базисная
переменная
![]() вместо
вместо
![]() .
Выполняется один шаг метода Гаусса:
вектор
.
Выполняется один шаг метода Гаусса:
вектор
![]() заменяется
на единичный вектор, с единицей на
заменяется
на единичный вектор, с единицей на
![]() -ом
месте.
-ом
месте.
– новые элементы направляющей строки:
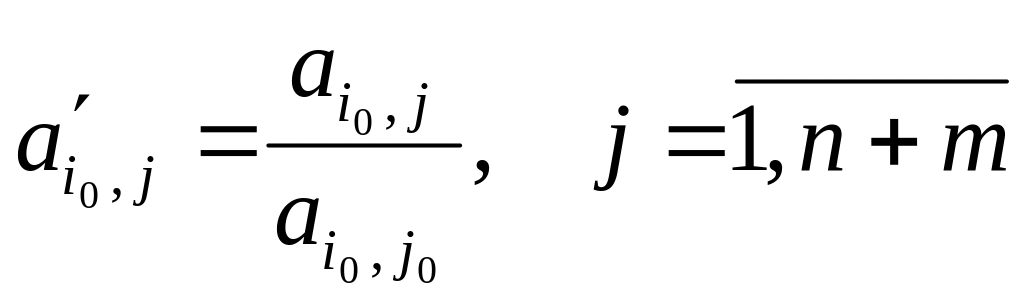 ;
–
новые значения остальных элементов
матрицы:
;
–
новые значения остальных элементов
матрицы:
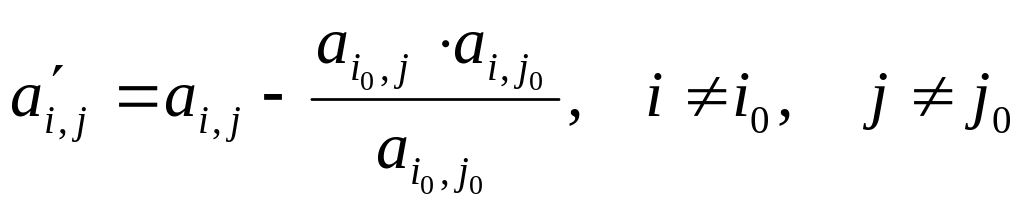 ;
;
– новые значения симплексных разностей:
![]() ;
–
вычисляем
;
–
вычисляем
![]()
Так получаем новую (k+1)-ую крайнюю точку. Переходим к Шагу 1.
