
Тема 2. Исследование и построение графиков функций.
Исследование функций и построение графиков удобно проводить по следующей схеме:
1) найти область определения;
2) отметить (если они есть) особенности функции (периодичность, четность и нечетность, сохранение знака), найти точки пересечения графика функции с осями координат;
3) исследовать функцию на непрерывность, найти точки разрыва;
4)
если граничные точки области определения
функции принадлежат ей, то найти значения
функции в этих точках, в противном
случае – выяснить поведение функции
в окрестности этих точек (включая и
несобственные точки
![]() и
и
![]() );
);
5) найти наклонные асимптоты (вертикальные и горизонтальные определяются в предыдущих пунктах ) или убедиться в их отсутствии;
6) найти участки возрастания и убывания функции, определить локальные экстремумы;
7) найти интервалы, на которых функция выпукла вверх или вниз, определить точки перегиба;
8) построить график функции.
Результаты исследования функции целесообразно свести в таблицу, а построение графика начать с нанесения асимптот, точек пересечения с осями координат, точек локального экстремума функции, точек перегиба и фрагментов графика функции вблизи этих точек и вблизи асимптот.
Пример
1. Исследовать функцию и построить ее
график:
![]() .
.
Решение. Исследование функции будем проводить, придерживаясь приведенной выше схемы.
1)
Функция определена на всей числовой
прямой, кроме точки
![]() .
.
2)
Так как
![]() и
и
![]() ,
то данная функция является функцией
общего вида. Очевидно, что эта функция
непериодическая. При
,
то данная функция является функцией
общего вида. Очевидно, что эта функция
непериодическая. При
![]()
![]() ,
при
,
при
![]()
![]() ,
следовательно,
,
следовательно,
![]() и
и
![]() -
точки пересечения графика функции с
осями координат.При
-
точки пересечения графика функции с
осями координат.При
![]()
![]() (здесь, конечно,
(здесь, конечно,
![]() ),
при
),
при
![]()
![]() .
.
3)
В точке
![]() 1
функция имеет разрыв второго рода, ибо
1
функция имеет разрыв второго рода, ибо
![]()
![]() ,
в остальных точках она непрерывна.
Прямая
является вертикальной асимптотой.
,
в остальных точках она непрерывна.
Прямая
является вертикальной асимптотой.
4)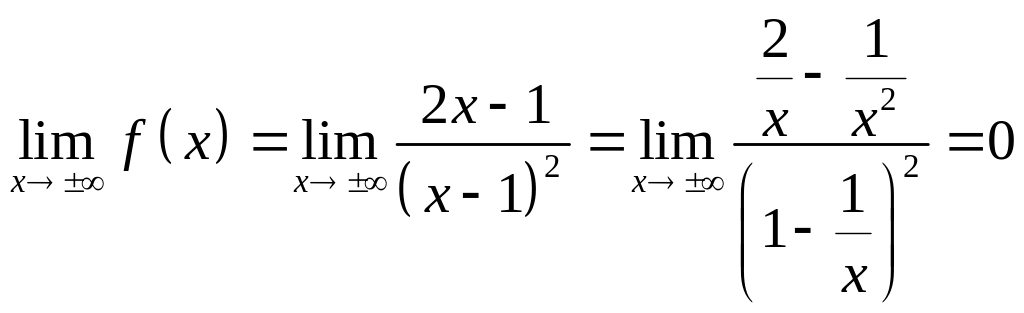 ,
следовательно, прямая
-
горизонтальная асимптота.
,
следовательно, прямая
-
горизонтальная асимптота.
5)
Найдем наклонные асимптоты:
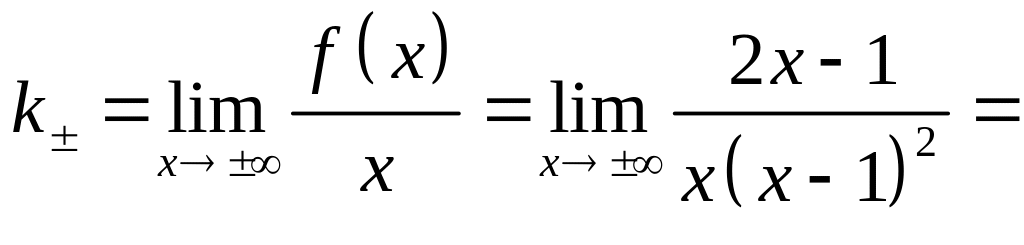
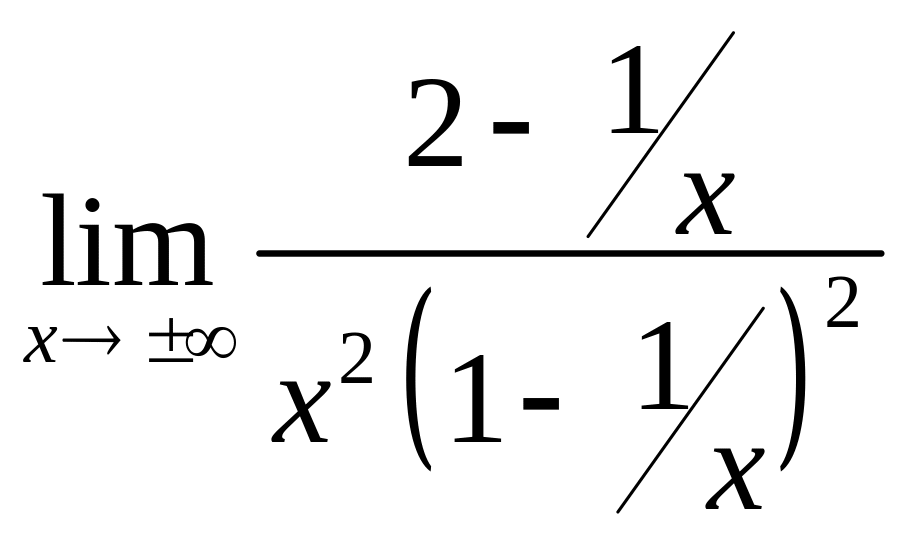 =
=
=0,
тогда
![]() ,
,
![]()
![]() ,
тогда
,
тогда
![]() .
Следовательно,
.
Следовательно,
![]() -наклонная
асимптота (она уже была найдена в п. 4 в
качестве горизонтальной).
-наклонная
асимптота (она уже была найдена в п. 4 в
качестве горизонтальной).
6)
Для нахождения участков монотонности
и экстремальных точек найдем первую
производную функции:
 .
.
Производная
![]() не существует при
(точка разрыва, см. п. 3) и
=0
при
.
Область определения функции разобьем
на интервалы
не существует при
(точка разрыва, см. п. 3) и
=0
при
.
Область определения функции разобьем
на интервалы
![]() и определим знак
в каждом из них. Для удобства вычислений
в интервале
и определим знак
в каждом из них. Для удобства вычислений
в интервале
![]() возьмем
возьмем
![]() :
:
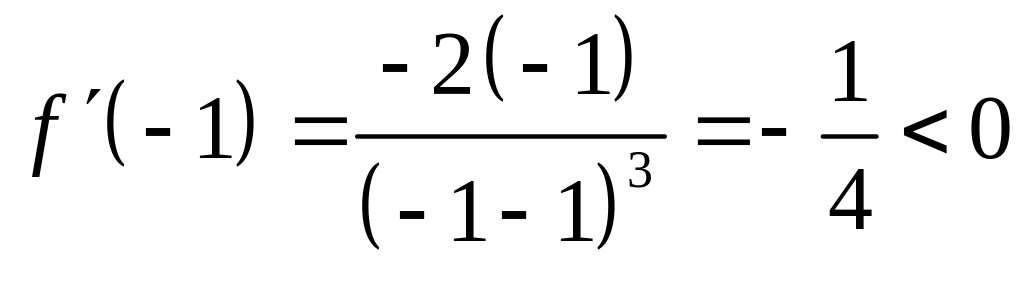 .
Значит, на этом интервале функция
убывает. На интервале
.
Значит, на этом интервале функция
убывает. На интервале
![]() удобно взять
удобно взять
![]() :
:
![]() следовательно, на интервале
функция возрастает. Наконец, на интервале
следовательно, на интервале
функция возрастает. Наконец, на интервале
![]() удобно взять
удобно взять
![]() :
:
![]() .
Значит, здесь функция убывает ( рис. 1).
.
Значит, здесь функция убывает ( рис. 1).


Рис.
1. Знак
![]() Рис.
2. Знак
Рис.
2. Знак
![]()
Так
как функция в точке
определена и непрерывна и при переходе
через нее
меняет знак с плюса на минус (что хорошо
видно на рис. 1) то в этой точке локальный
минимум, причем
![]() .
.
7)
Для нахождения участков выпуклости
найдем вторую производную функции
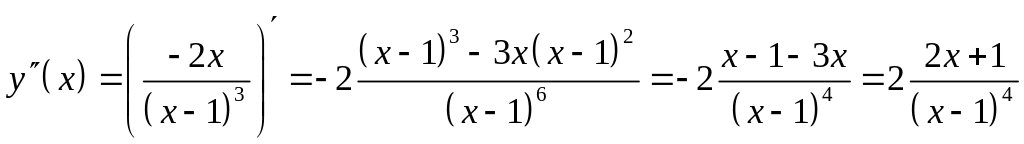 .
Она не существует в точке
(в этой точке функция не определена
(см. п. 1)) и равна нулю при
.
Она не существует в точке
(в этой точке функция не определена
(см. п. 1)) и равна нулю при
![]() . Область определения функции разобьем
на интервалы
. Область определения функции разобьем
на интервалы
![]() и определим знак
и определим знак
![]() в каждом из них (рис. 2). Для простоты
вычислений удобно взять
в каждом из них (рис. 2). Для простоты
вычислений удобно взять
![]() и
и
![]() .
Тогда
.
Тогда
![]() ,
следовательно, на интервале
,
следовательно, на интервале
![]() функция выпукла вверх;
функция выпукла вверх;
![]() ,
значит, на интервале
она выпукла вниз;
,
значит, на интервале
она выпукла вниз;
![]() ,
следовательно, на интервале
,
следовательно, на интервале
![]() функция выпукла вниз. При переходе
через точки
и
вторая производная меняет знак,
следовательно, это точки перегиба
функции (
функция выпукла вниз. При переходе
через точки
и
вторая производная меняет знак,
следовательно, это точки перегиба
функции (![]() ).
).
Результаты проведенного исследования сведем в таблицу:
x |
( |
|
( |
0 |
(0,1) |
1 |
( |
y, |
|
|
|
0 |
+ |
разрыв |
|
y,, |
|
0 |
+ |
|
+ |
+ |
|
y |
|
|
|
|
|
|
10) Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот (рис. 3).
В окончательном виде график изображен на рис. 4.


Рис.3 Рис.4
Пример
2. Исследовать функцию и построить ее
график:
![]() .
.
Решение. Вновь используем приведенную выше схему.
1) Функция определена на всей числовой оси.
2)
Так как
![]() и
и
![]() ,
то данная функция общего вида. Функция
непериодическая. Если
,
то
;
если
,
то
,
то данная функция общего вида. Функция
непериодическая. Если
,
то
;
если
,
то
![]() .
Следовательно, О(0,0) и М(5,0)- точки
пересечения графика функции с осями
координат. Кроме того,
при
.
Следовательно, О(0,0) и М(5,0)- точки
пересечения графика функции с осями
координат. Кроме того,
при
![]() и
при
и
при
![]() .
.
3) Функция непрерывна на всей числовой оси.
4)
![]() .
.
5) Найдем наклонные асимптоты:
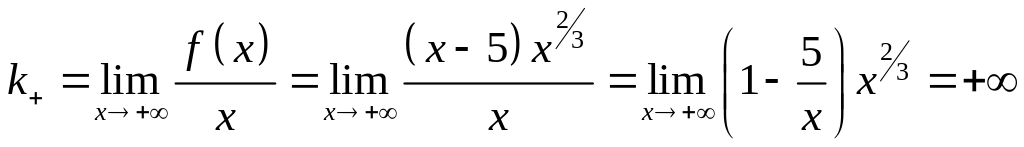 ;
;
![]() .
.
Следовательно, наклонных асимптот нет.
6)
![]() .
Следовательно,
.
Следовательно,
![]() при
при![]() и
и
![]() ;
;
![]() при
при
![]() .
.
7)
![]() .
Следовательно,
.
Следовательно,
![]() при
при
![]() и
;
и
;
![]() при
при
![]() .
.
Итак,
функция
определена на всей числовой прямой.
График ее пересекает ось
![]() в точках
и
в точках
и
![]() .
Асимптот нет. На промежутках
и
.
Асимптот нет. На промежутках
и
![]() функция возрастает, на промежутке
функция возрастает, на промежутке
![]() -
убывает, в точке
-
убывает, в точке
![]() имеет локальный максимум, в точке
имеет локальный максимум, в точке
![]() -
локальный минимум. На промежутках
-
локальный минимум. На промежутках
![]() и
и
![]() функция выпукла вниз, на промежутке
функция выпукла вниз, на промежутке
![]() -
выпукла вверх. Точка
-
выпукла вверх. Точка
![]() -
точка перегиба. Поскольку
непрерывна в нуле и
-
точка перегиба. Поскольку
непрерывна в нуле и
![]()
![]() ,
,
![]() ,
,
то
полупрямая
![]() является и левой и правой полукасательной
к графику функции в точке
.
Следовательно, точка
-
точка возврата кривой. График данной
функции представлен на рис.5.
является и левой и правой полукасательной
к графику функции в точке
.
Следовательно, точка
-
точка возврата кривой. График данной
функции представлен на рис.5.
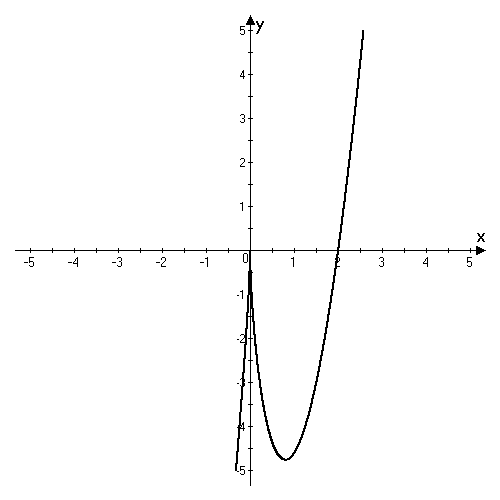
Рис. 5
Пример 3. Исследовать и построить график кривой, заданной параметрически
![]() .
.
Решение.
Параметрические соотношения определяют
функцию
![]() ,
однозначную и непрерывную на тех
промежутках изменения параметра
,
однозначную и непрерывную на тех
промежутках изменения параметра
![]() ,
на которых функция
,
на которых функция
![]() непрерывна и строго монотонна. Выделим
такие промежутки. Для этого и для
дальнейших исследований построим
графики функций
и
непрерывна и строго монотонна. Выделим
такие промежутки. Для этого и для
дальнейших исследований построим
графики функций
и
![]() .
Найдем производные этих функций. Имеем
.
Найдем производные этих функций. Имеем
 .
.
Функция
определена и непрерывна при
![]() ,
причем
,
причем
![]() -
вертикальные асимптоты при
-
вертикальные асимптоты при
![]() соответственно. Из равенства
=
соответственно. Из равенства
=![]() следует, что
-
горизонтальная асимптота. Из вида
производной устанавливаем, что
строго монотонна на четырех промежутках:
следует, что
-
горизонтальная асимптота. Из вида
производной устанавливаем, что
строго монотонна на четырех промежутках:
![]() .
На первых двух промежутках
.
На первых двух промежутках
![]() и, следовательно, на этих промежутках
убывает. Аналогично устанавливаем, что
на промежутках (0,1), (1,+
и, следовательно, на этих промежутках
убывает. Аналогично устанавливаем, что
на промежутках (0,1), (1,+![]() )
функция
возрастает. График функции
изображен на рис. 6.
)
функция
возрастает. График функции
изображен на рис. 6.
Функция
определена и непрерывна при всех
значениях
,
кроме
![]() ,
причем
-
вертикальная асимптота. Из равенств
,
причем
-
вертикальная асимптота. Из равенств
![]() видно, что
-
горизонтальная асимптота и при
видно, что
-
горизонтальная асимптота и при
![]() и при
и при
![]() .
В силу выполнения неравенства
.
В силу выполнения неравенства
![]() на промежутках
на промежутках
![]() функция
убывает; на промежутке
функция
убывает; на промежутке
![]() имеем
имеем
![]() и, значит, функция
здесь возрастает. Точка
и, значит, функция
здесь возрастает. Точка
![]() является точкой локального максимума.
График функции
изображен на рис. 7.
является точкой локального максимума.
График функции
изображен на рис. 7.

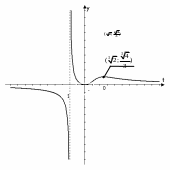
Рис. 6 Рис. 7
Итак,
данные в примере функции
и
определяют функцию
на каждом из промежутков
.
Фактически, мы здесь разбиваем
параметрически заданную в примере
кривую на участки, каждый из которых
является графиком некоторой функции
.
Построив графики этих функций, мы тем
самым построим и саму кривую (каждую
из функций
принято называть однозначной ветвью
функции, заданной параметрически). Так
как формальное дифференцирование на
всех промежутках производится одинаково,
то имеем при
![]()
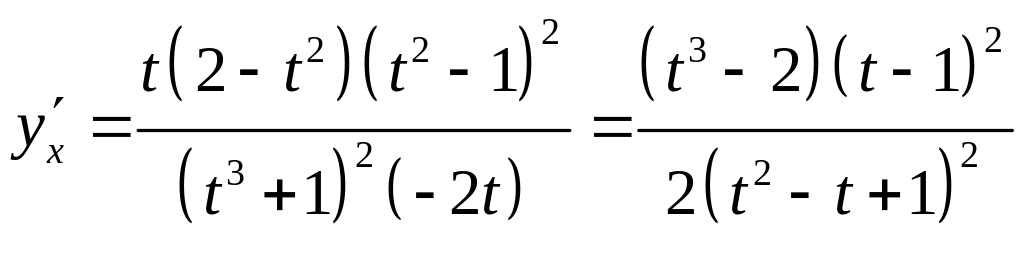 ,
,
 .
.
Теперь построим графики функций на каждом из промежутков . При построении используем графики функций и .
I.
![]() .
.
1)
![]() ;
;
2)-4)
;
условие
![]() эквивалентно на промежутке
условию
,
поэтому
эквивалентно на промежутке
условию
,
поэтому
![]() ;
точно так же
;
точно так же
![]() ;
;
5)
![]() ;
;
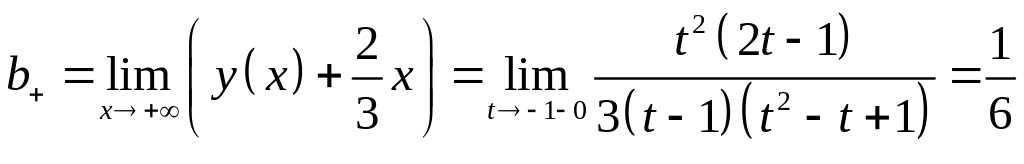 ;
;
6)
![]() ,
так как
,
так как
![]() ;
;
7)
![]() ,
так как многочлен
,
так как многочлен
![]()
![]() при
(
при
(![]() при любом
и поэтому функция
при любом
и поэтому функция
![]() возрастает при
возрастает при
![]() ;
единственная точка
;
единственная точка
![]() такая, что
такая, что
![]() ,
то есть нуль функции
,
принадлежит промежутку
,
то есть нуль функции
,
принадлежит промежутку
![]() ,
так как
,
так как
![]() ,
,
![]()
![]() ).
).
Таким
образом, ветвь кривой, соответствующая
изменению
на промежутке
,
представляет собой график непрерывной,
отрицательной, монотонно убывающей,
выпуклой вниз на луче
функции с асимптотой
![]() и краевым условием
и краевым условием
![]() .
График ветви кривой изображен на рис.
8.
.
График ветви кривой изображен на рис.
8.

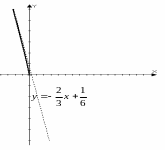
Рис. 8 Рис. 9
Здесь и далее в этом примере (рис.8-12) для наглядности масштаб по оси Y сделан в 3 раза больше чем масштаб по оси X.
II.
![]() .
.
1)
![]() ;
;
2)-4)
![]() ;
условие
;
условие
![]() эквивалентно на промежутке
эквивалентно на промежутке
![]() условию
условию
![]() ,
поэтому
,
поэтому
![]() ,
значению
соответствует значение
,
значению
соответствует значение
![]() ,
следовательно, значение
,
следовательно, значение
![]() при
равно 0;
при
равно 0;
5)
![]() ;
;
6)
,
так как
;
![]() ;
;
7)
![]() .
.
Итак,
ветвь кривой, соответствующая изменению
на промежутке
представляет график непрерывной,
неотрицательной, монотонно убывающей,
выпуклой вверх на луче
функции с асимптотой
и краевым минимумом
![]() имеющей в точке
левую полукасательную: луч
имеющей в точке
левую полукасательную: луч
![]() .
График ветви кривой изображен на рис.
9.
.
График ветви кривой изображен на рис.
9.
III.
![]() .
.
1) ;
2)-4)
;
условие
эквивалентно на промежутке
![]() условию
условию
![]() ,
поэтому
,
поэтому
![]() ,
следовательно,
,
следовательно,
![]() -горизонтальная
асимптота; значению
соответствует значение
;
-горизонтальная
асимптота; значению
соответствует значение
;
5)
случай
уже
исследован в предыдущем пункте, а случай
![]() рассматривать не надо (у нас
и
);
рассматривать не надо (у нас
и
);
6)
,
так как
;
![]() ;
;
7) .
Итак,
ветвь кривой, соответствующая изменению
на промежутке
представляет график непрерывной,
неотрицательной, монотонно убывающей,
выпуклой вверх на луче
функции с асимптотой
![]() и краевым минимумом
имеющей в точке
левую полукасательную: луч
.
и краевым минимумом
имеющей в точке
левую полукасательную: луч
.
Таким образом, точка является общей точкой двух ветвей кривой, которые подходят к ней слева и сверху, и обе эти ветви имеют в точке общую левую полукасательную: луч . Точка является точкой возврата кривой. График ветви кривой изображен на рис. 10.

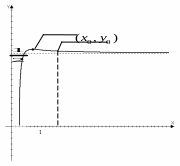
Рис. 10 Рис. 11
IV.
![]() .
.
1) ;
2)-4)
;
условие
эквивалентно на промежутке
условию
,
поэтому
![]() ;
аналогично
;
аналогично
![]() .
.
5) случай уже рассмотрен в предыдущем пункте, а случай исследовать не надо ( );
6)
![]() для
для
![]() ,
то есть для
,
то есть для
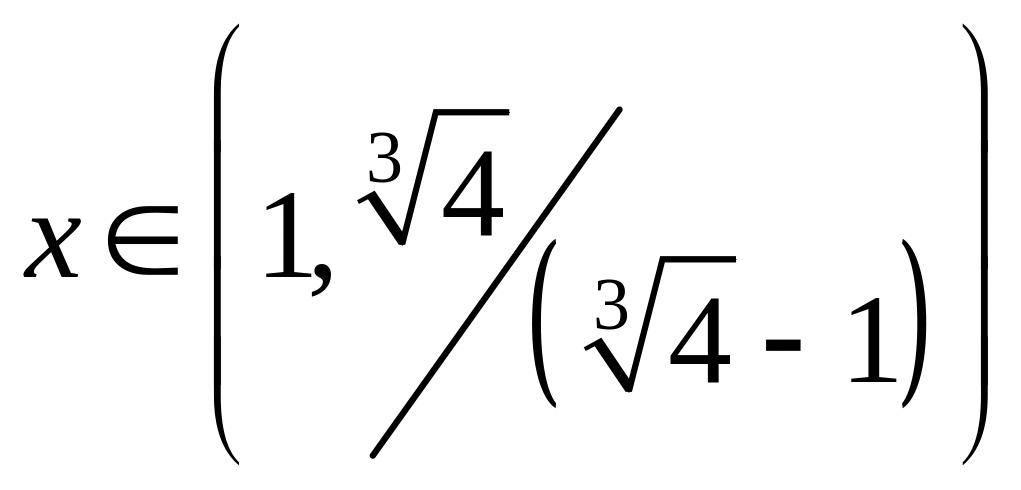 ;
для
;
для
![]() ,
то есть для
,
то есть для
![]() ;
точка
;
точка
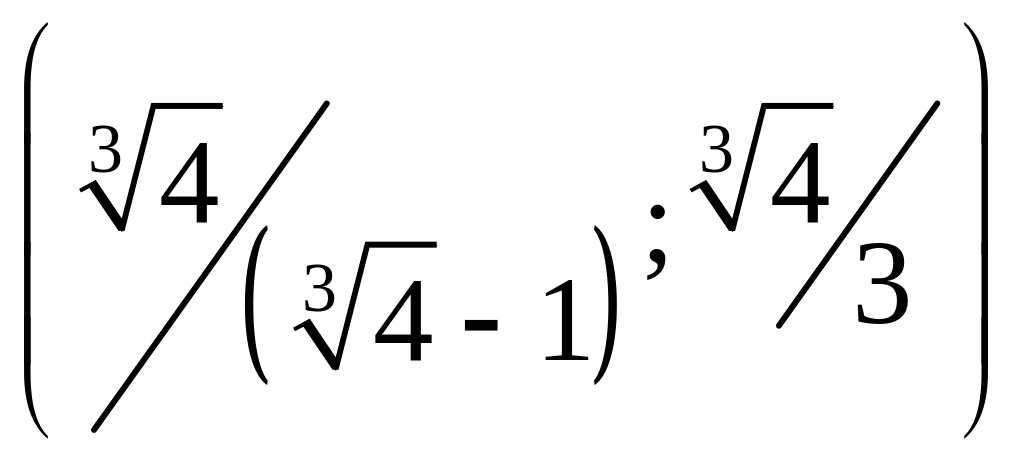 -
точка локального максимума;
-
точка локального максимума;
7)
для
![]() и
для
и
для
![]() ,
где
определено в п. I.
,
где
определено в п. I.
Итак,
ветвь кривой, соответствующая изменению
на промежутке
представляет собой график непрерывной,
положительной луче
функции с горизонтальной асимптотой
и краевым условием
.
На промежутке
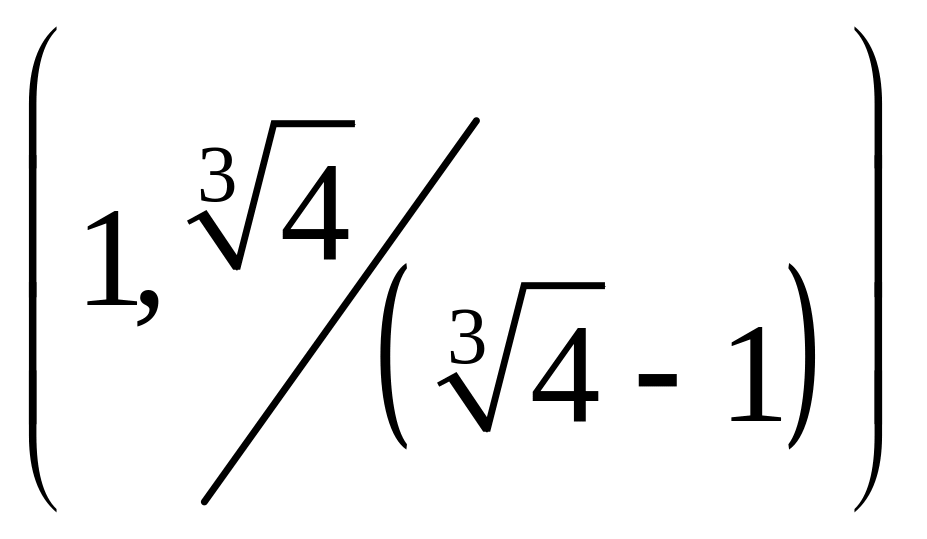 функция возрастает, на промежутке
функция возрастает, на промежутке
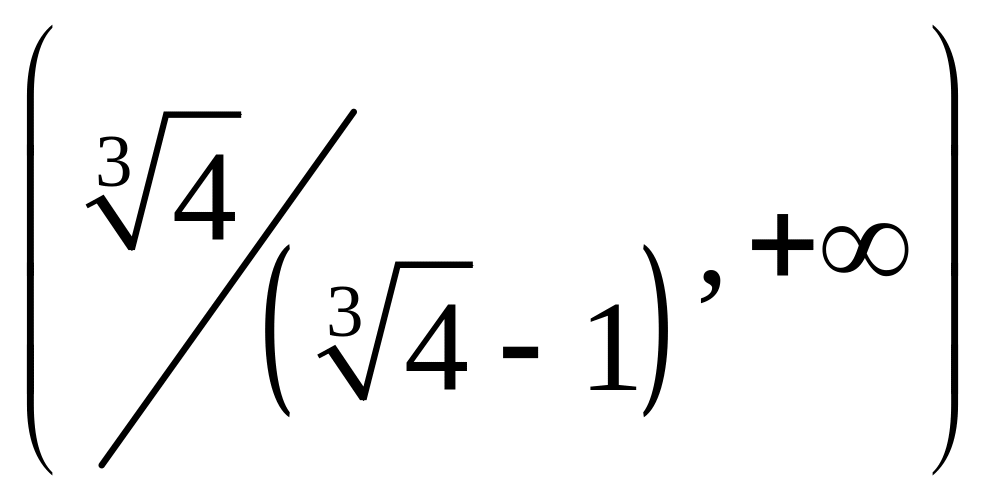 убывает, точка
-
точка локального максимума. Существует
точка
убывает, точка
-
точка локального максимума. Существует
точка
![]() ,
,
![]() такая, что на промежутке
такая, что на промежутке
![]() функция выпукла вверх, на промежутке
функция выпукла вверх, на промежутке
![]() -
выпукла вниз, точка
-
выпукла вниз, точка
![]() -
точка перегиба. Заметим еще, что при
параметрическом задании кривой, если
существуют пределы
-
точка перегиба. Заметим еще, что при
параметрическом задании кривой, если
существуют пределы
![]() ,
то точка
,
то точка
![]() также считается принадлежащей этой
кривой. Таким образом, в нашем случае
точка
также считается принадлежащей этой
кривой. Таким образом, в нашем случае
точка
![]() принадлежит кривой. График этой ветви
кривой изображен на рис. 11.
принадлежит кривой. График этой ветви
кривой изображен на рис. 11.
Прежде
чем объединить все сказанное и построить
данную в задаче кривую заметим следующее.
Имеем
![]() ,
для
и
,
для
и
![]() для
для
![]() .
Таким образом, ветвь кривой, подходящая
снизу к точке
,
в этой точке имеет правую полукасательную
– луч
.
Таким образом, ветвь кривой, подходящая
снизу к точке
,
в этой точке имеет правую полукасательную
– луч
![]() ;
ветвь кривой, подходящая сверху к точке
,
имеет в этой точке правую полукасательную
– луч
;
ветвь кривой, подходящая сверху к точке
,
имеет в этой точке правую полукасательную
– луч
![]() .
Угол между этими лучами равен
.
Угол между этими лучами равен
![]() ,
следовательно, кривая имеет в точке
вертикальную касательную
.
,
следовательно, кривая имеет в точке
вертикальную касательную
.
Окончательный график кривой изображен на рис. 12.
Скажем
теперь несколько слов о нахождении
наибольшего и наименьшего значений
функции. Если функция
![]() непрерывна на замкнутом промежутке
непрерывна на замкнутом промежутке
![]() ,
то она достигает на нем своих наибольшего
и наименьшего значений. Наибольшее и
наименьшее значения функции достигаются
либо в критических точках, лежащих
внутри промежутка, либо на его концах.
Чтобы найти наибольшее и наименьшее
значения функции
,
следует вычислить ее значения в
критических точках, лежащих внутри
и в точках
,
то она достигает на нем своих наибольшего
и наименьшего значений. Наибольшее и
наименьшее значения функции достигаются
либо в критических точках, лежащих
внутри промежутка, либо на его концах.
Чтобы найти наибольшее и наименьшее
значения функции
,
следует вычислить ее значения в
критических точках, лежащих внутри
и в точках
![]() и
и
![]() ,
затем выбрать среди них наибольшее и
наименьшее. Отметим в связи с этим
следующие два положения. Если в промежутке
,
затем выбрать среди них наибольшее и
наименьшее. Отметим в связи с этим
следующие два положения. Если в промежутке
![]() ,
конечном или бесконечном, одна критическая
точка и в ней локальный максимум
(минимум), то в ней наибольшее (наименьшее)
значение. Если функция задана и непрерывна
на некотором промежутке, не являющемся
замкнутым, то среди значений функции
на этом промежутке может не быть
наибольшего и наименьшего.
,
конечном или бесконечном, одна критическая
точка и в ней локальный максимум
(минимум), то в ней наибольшее (наименьшее)
значение. Если функция задана и непрерывна
на некотором промежутке, не являющемся
замкнутым, то среди значений функции
на этом промежутке может не быть
наибольшего и наименьшего.

Рис.12
Пример 4. Найти наибольшее и наименьшее значения функции на указанных промежутках:
1)
![]() на
на
![]() ;
;
2)
![]() на
на
![]() ;
;
3)
![]() на
на
![]() .
.
Решение.
1)
Найдем производную
![]() .
Она обращается в нуль в точке
,
эта точка лежит внутри отрезка
.
Для отыскания наибольшего и наименьшего
значений функции необходимо вычислить
значения функции в точке
и на концах промежутка
.
Она обращается в нуль в точке
,
эта точка лежит внутри отрезка
.
Для отыскания наибольшего и наименьшего
значений функции необходимо вычислить
значения функции в точке
и на концах промежутка
![]() .
Находим
.
Находим
![]() ,
,![]() ,
,
![]() .
Значит, наименьшее значение равно -7,
наибольшее равно 2.
.
Значит, наименьшее значение равно -7,
наибольшее равно 2.
2)
Найдем производную
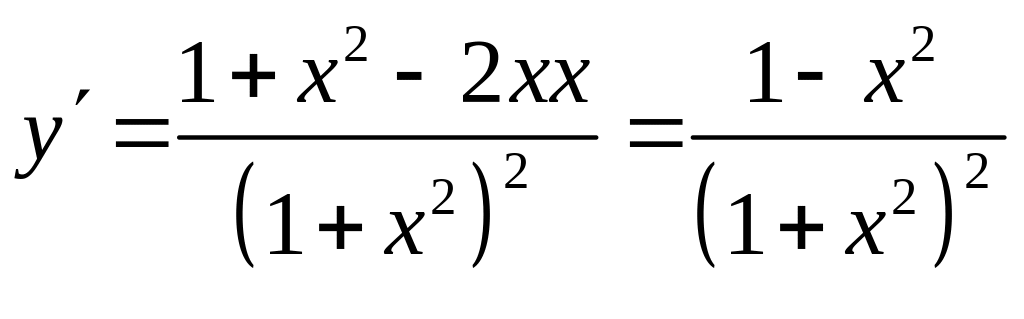 .
Она равна нулю в точках
.
Она равна нулю в точках
![]() .
Вычислим
.
Вычислим
![]() .
Поскольку
.
Поскольку
![]()
 ,
то наименьшее значение равно -
,
то наименьшее значение равно -![]() ,
наибольшее равно
.
,
наибольшее равно
.
3)
Найдем производную
![]() .
Она обращается в нуль при
.
Она обращается в нуль при
![]() .
Точка
не лежит внутри промежутка
.
Для отыскания наибольшего и наименьшего
значений необходимо вычислить значения
функции на концах промежутка. Имеем
.
Точка
не лежит внутри промежутка
.
Для отыскания наибольшего и наименьшего
значений необходимо вычислить значения
функции на концах промежутка. Имеем
![]() .
Следовательно, наибольшее значение
равно
.
Следовательно, наибольшее значение
равно
![]() ,
наименьшее значение равно 0.
,
наименьшее значение равно 0.
К задачам на наибольшее и наименьшее значения часто относят так называемые текстовые задачи. Это задачи, в которых требуется описать с помощью функции какие-нибудь геометрическое свойство, физическое явление и тому подобное, а затем найти экстремальные значения построенной функции. Приведем несколько примеров таких задач.
Пример 5. Положительное число разложить на два положительных слагаемых так, чтобы сумма их кубов была наименьшей.
Решение.
Пусть первое слагаемое равно
,
тогда второе слагаемое равно
![]() .
Составим функцию
.
Составим функцию
![]() .
По смыслу задачи
.
По смыслу задачи
![]() .
Задача свелась к нахождению наименьшего
значения функции на отрезке
.
Задача свелась к нахождению наименьшего
значения функции на отрезке
![]() .
Найдем производную
.
Найдем производную
![]() .
Производная обращается в нуль в точке
.
Производная обращается в нуль в точке
![]() .
Так как
.
Так как
![]()
![]() ,
то в точке
функция имеет локальный минимум.
Поскольку функция имеет одну критическую
точку и в ней минимум, то в этой точке
наименьшее значение. Итак, сумма кубов
будет наименьшей, если слагаемые равны
друг другу и равны
,
то в точке
функция имеет локальный минимум.
Поскольку функция имеет одну критическую
точку и в ней минимум, то в этой точке
наименьшее значение. Итак, сумма кубов
будет наименьшей, если слагаемые равны
друг другу и равны
![]() .
.
Пример
6. В эллипс
![]() вписать прямоугольник наибольшей
площади со сторонами , параллельными
осям эллипса.
вписать прямоугольник наибольшей
площади со сторонами , параллельными
осям эллипса.
Решение.
Пусть
и
- длины полусторон прямоугольника.
Тогда
![]() ,
причем
и
- координаты точки, лежащей на эллипсе.
Для упрощения следует записать
параметрические уравнения эллипса:
,
причем
и
- координаты точки, лежащей на эллипсе.
Для упрощения следует записать
параметрические уравнения эллипса:
![]() .
Тогда
.
Тогда
![]() ,
откуда
,
откуда
![]() при
при
![]() ,
а
,
а
![]() .
.
Пример 7. Суточные расходы при плавании судна состоят из двух частей: постоянной, равной руб., и переменной, возрастающей пропорционально кубу скорости. При какой скорости плавание судна будет наиболее экономичным ?
Решение.
Предположим, что судно прошло
![]() км
за
км
за
![]() суток. Тогда расходы
суток. Тогда расходы
![]() будут равны
будут равны
![]() ,
где
,
где
![]() -
коэффициент пропорциональности. Но
так как
-
коэффициент пропорциональности. Но
так как
![]() ,
то
,
то
![]() .
.
Проводя
обычные исследования на наименьшее
значение, находим скорость, при которой
расходы минимальны:
![]() .
.
Контрольные задания к теме 2.
Исследование и построение графиков функций.
Задание 1: Исследовать функции и построить графики.
а).
 ,
б).
,
б).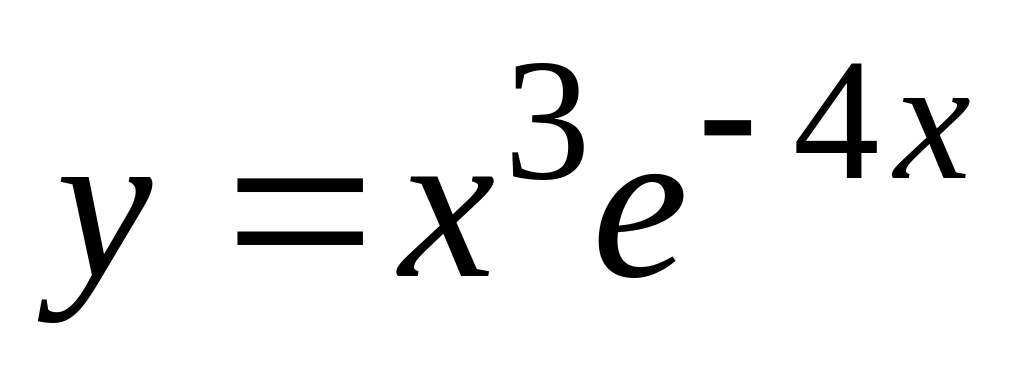 ,
в).
,
в).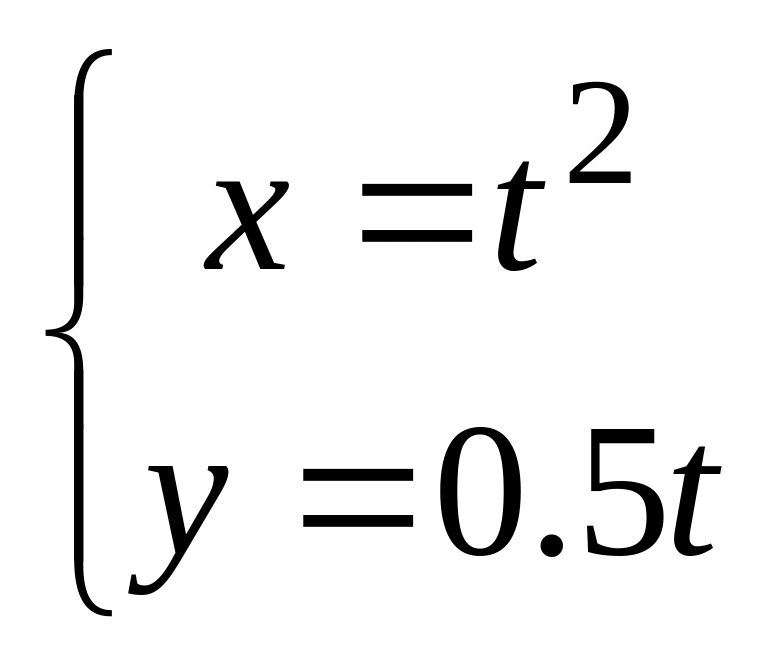 .
.а).
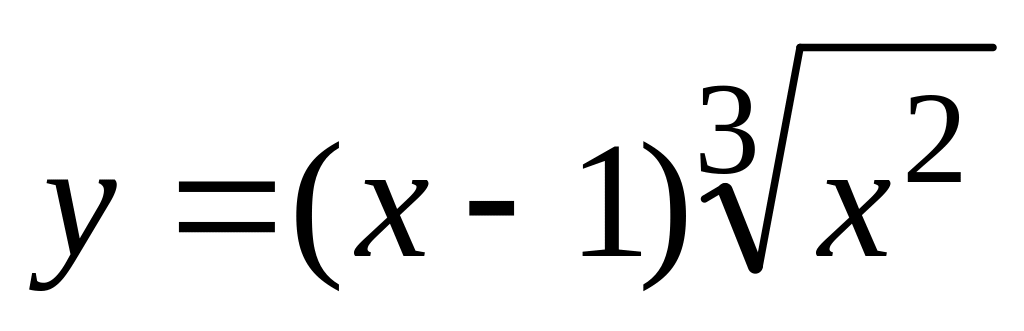 ,
б).
,
б).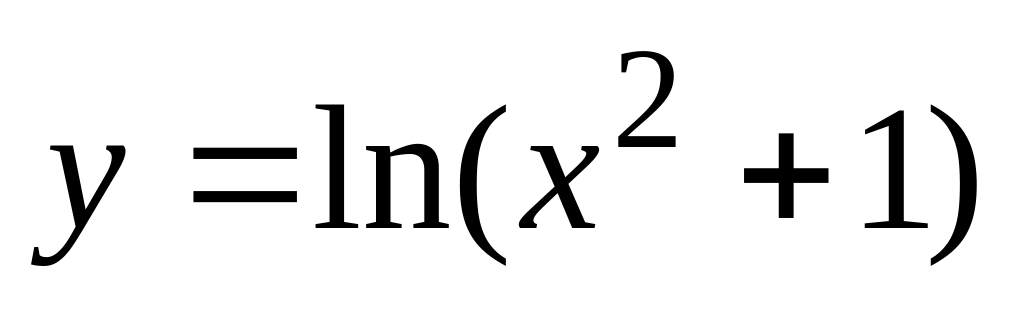 ,
в).
,
в).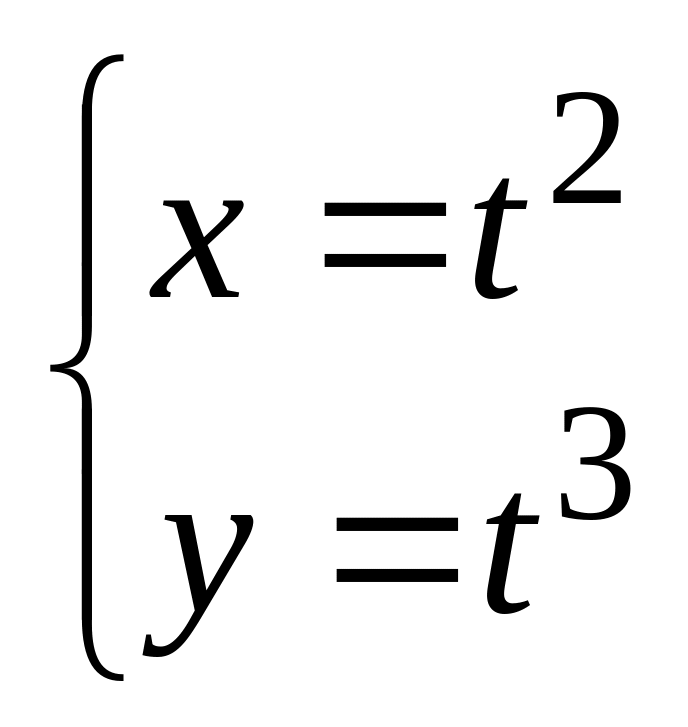 .
.а).
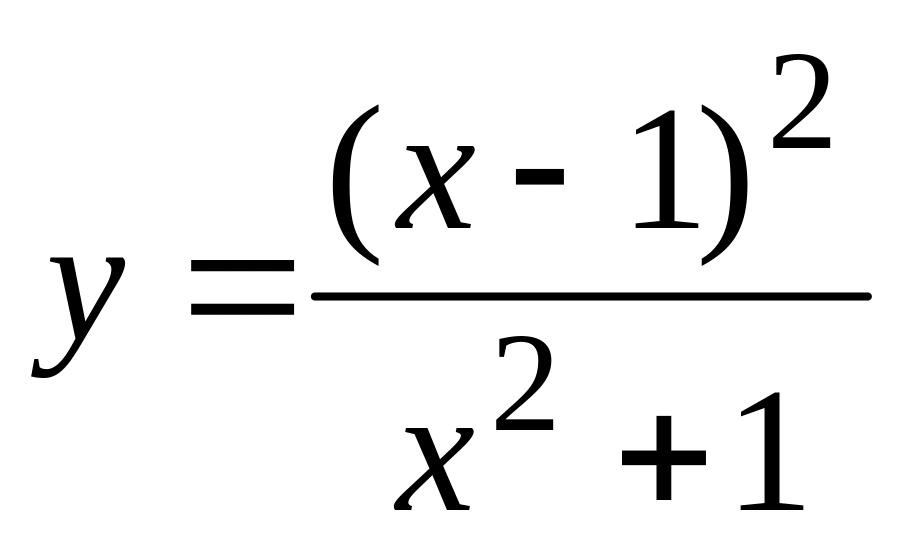 ,
б)
,
б) ,
в).
,
в).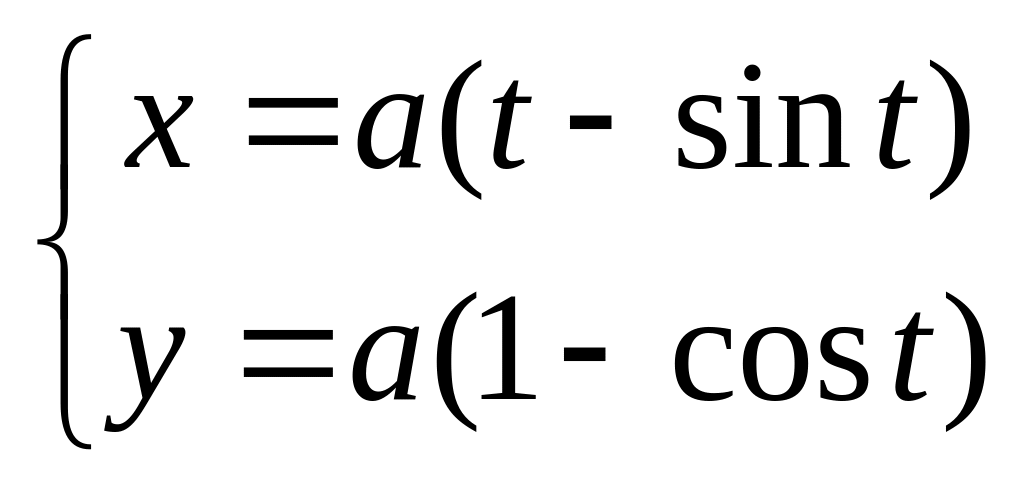 .
.а).
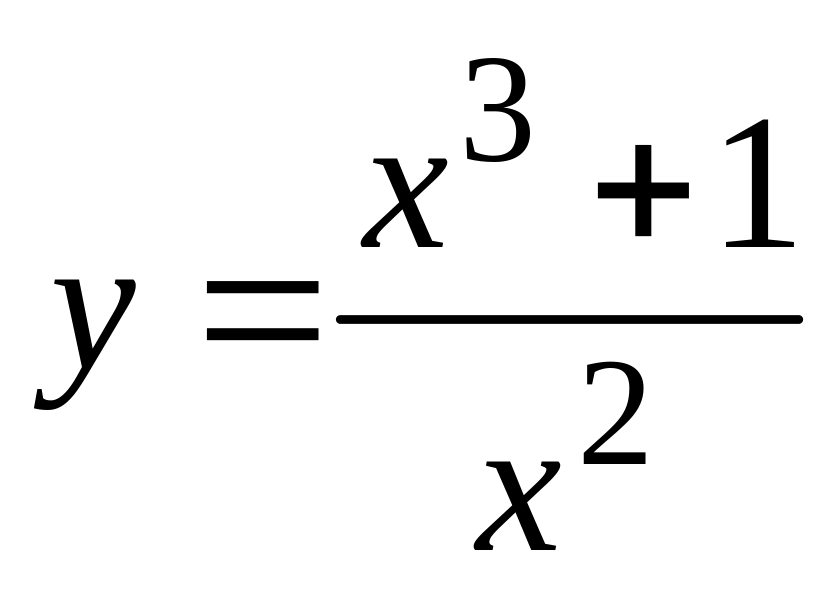 ,
б).
,
б).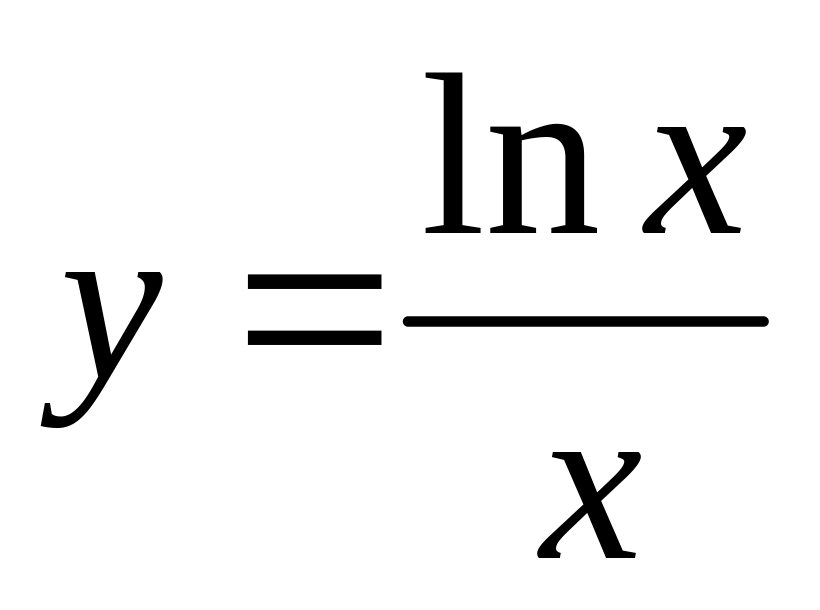 ,
в).
,
в).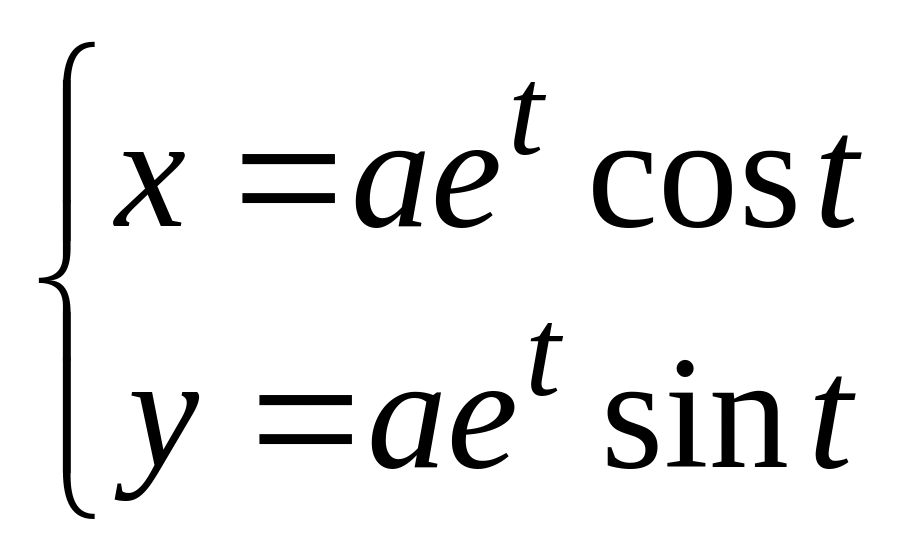 .
.а).
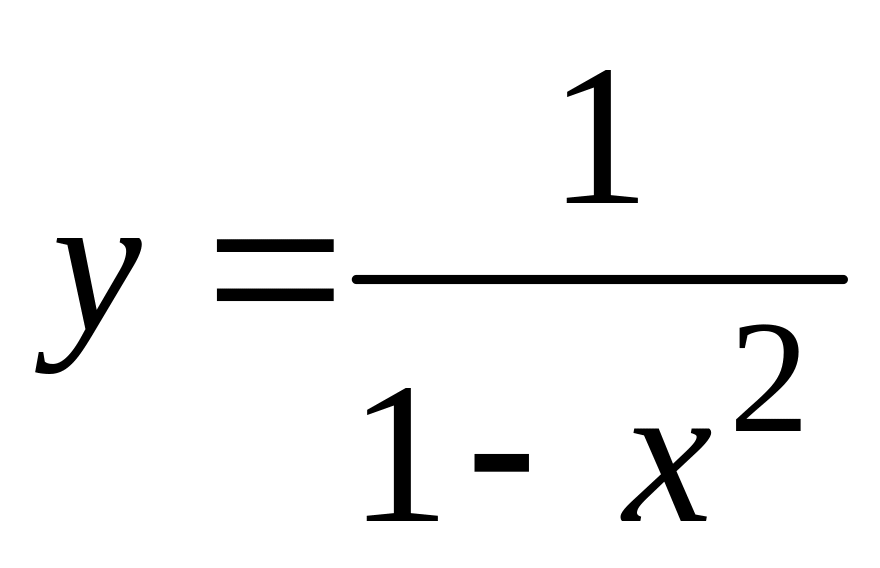 ,
б).
,
б).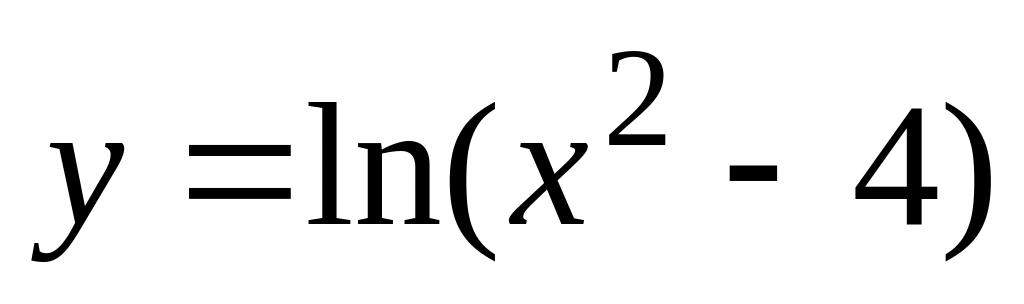 ,
в).
,
в).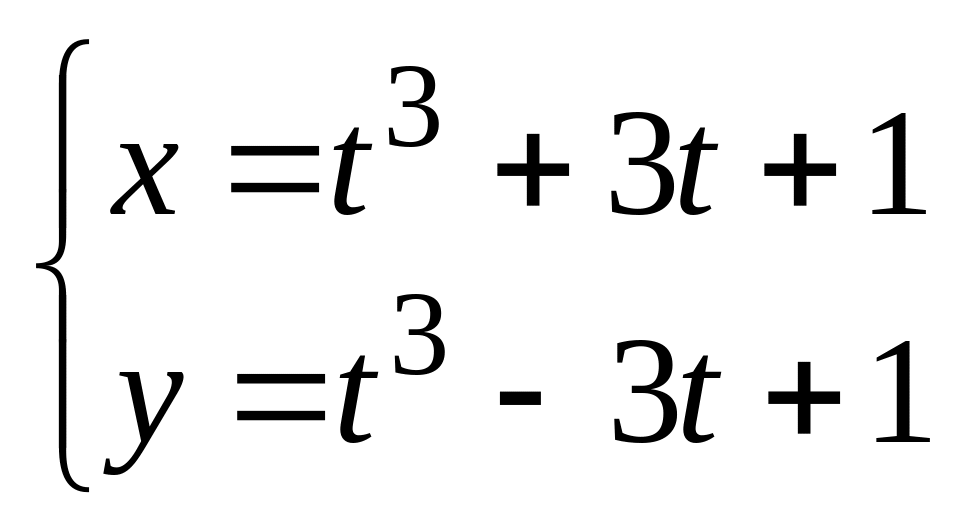 .
.а).
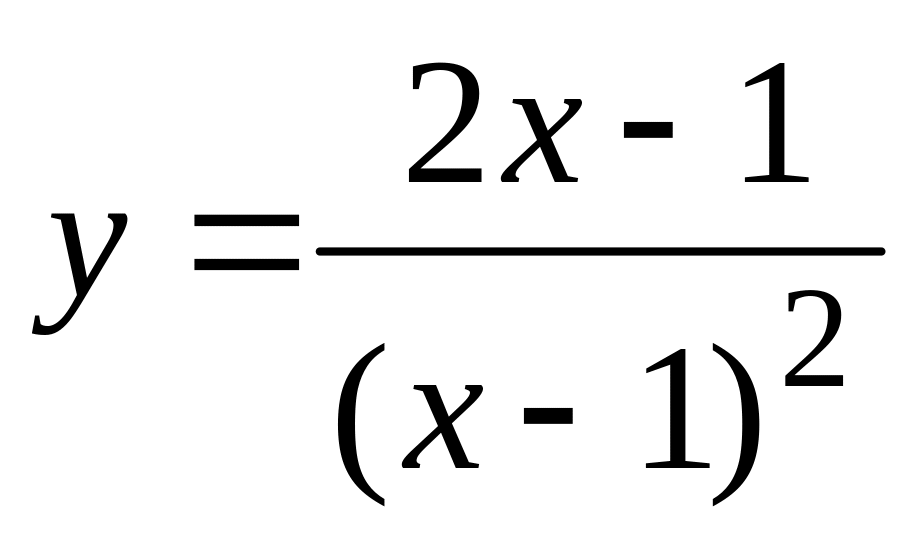 ,
б).
,
б). ,
в).
,
в).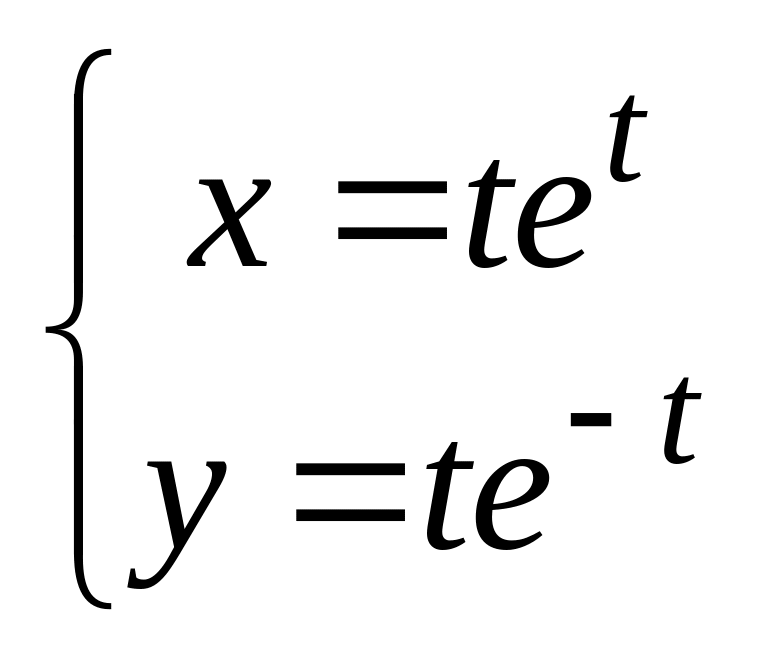 .
.а).
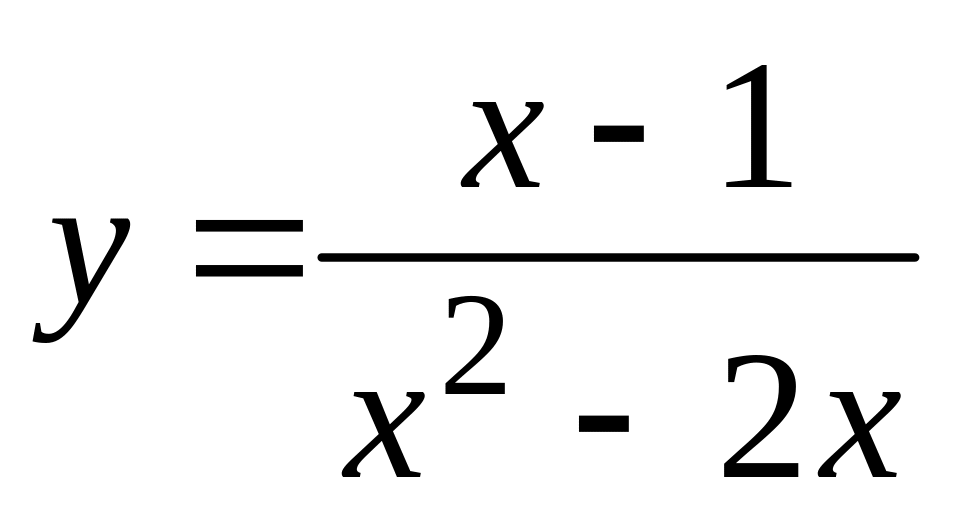 ,
б).
,
б). ,
в).
,
в). .
.а).
 ,
б).
,
б).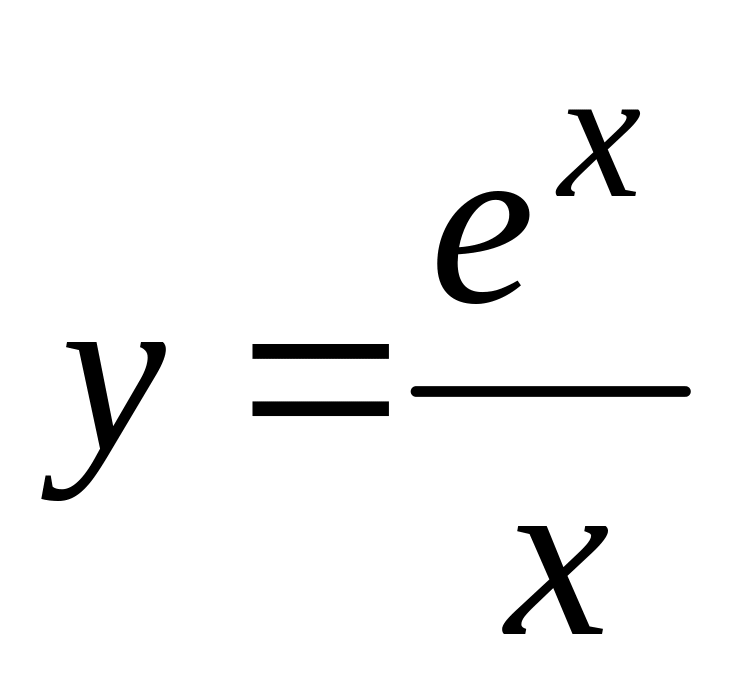 ,
в).
,
в). .
.а).
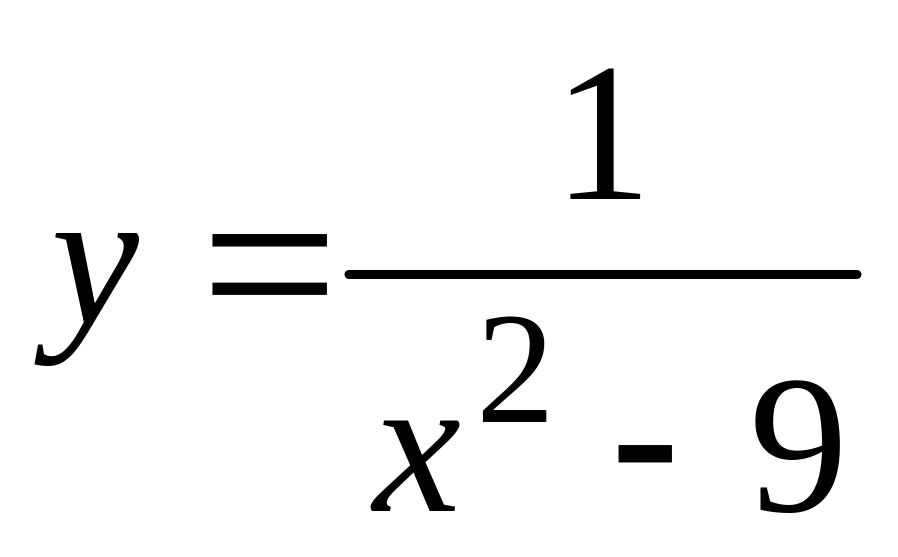 ,
б).
,
б).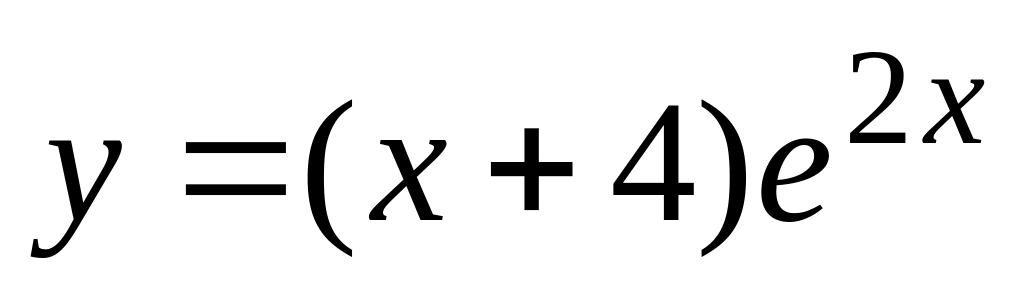 ,
в).
,
в).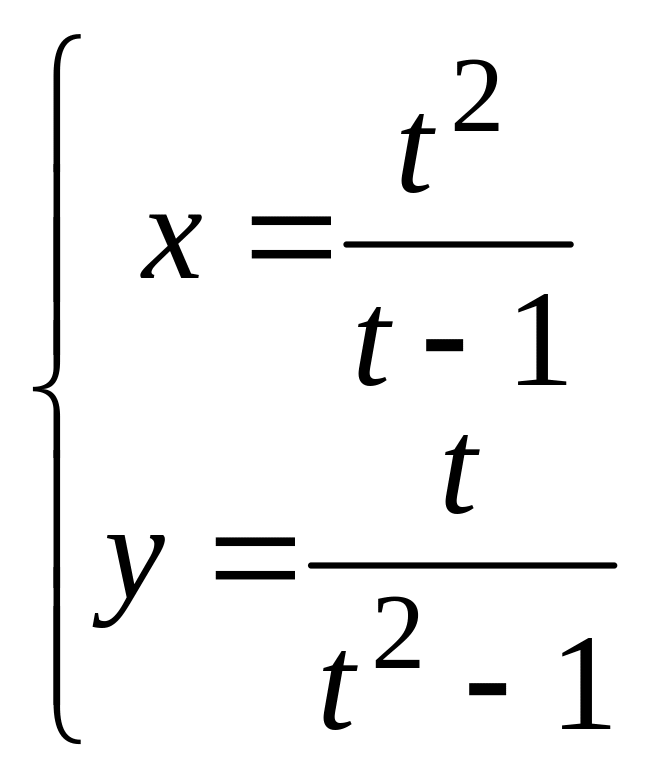 .
.а).
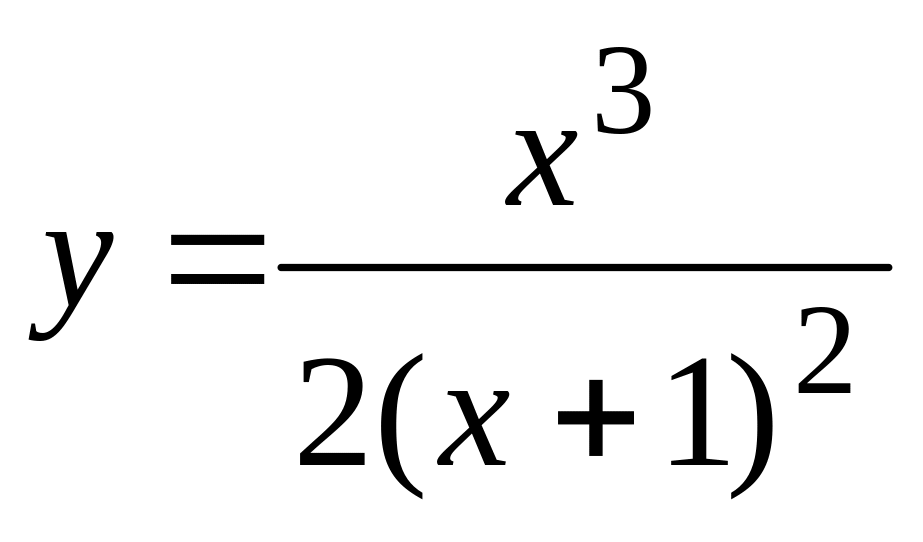 ,
б).
,
б). ,
в).
,
в).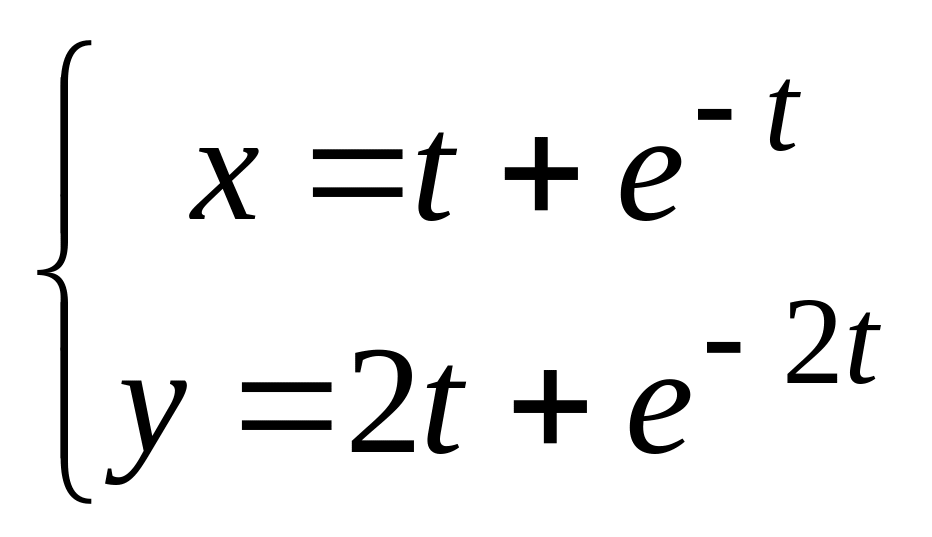 .
.а).
 ,
б).
,
б).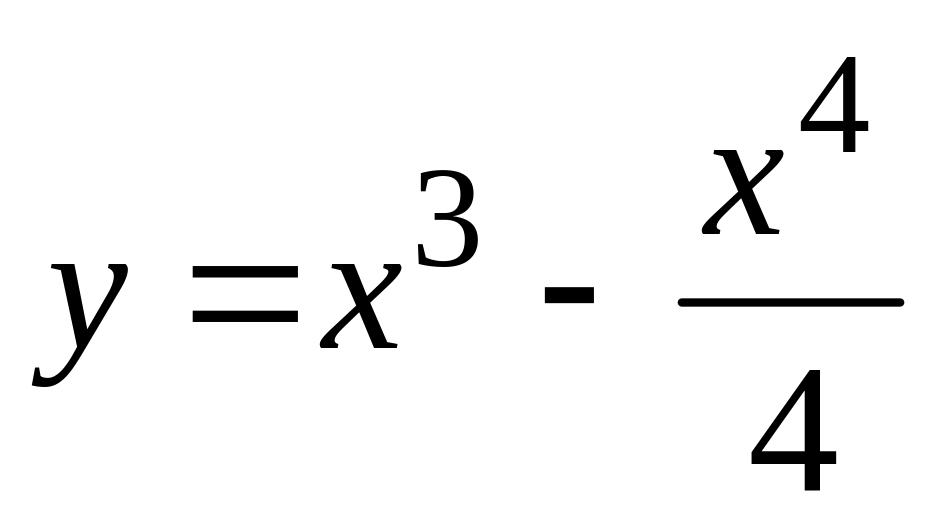 ,
в).
,
в). .
.а).
 ,
б).
,
б).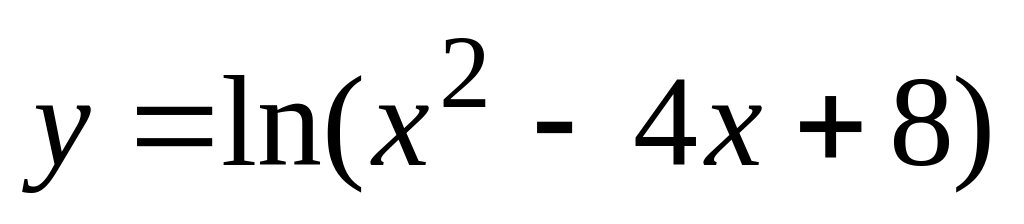 ,
в).
,
в). .
.а).
 ,
б).
,
б).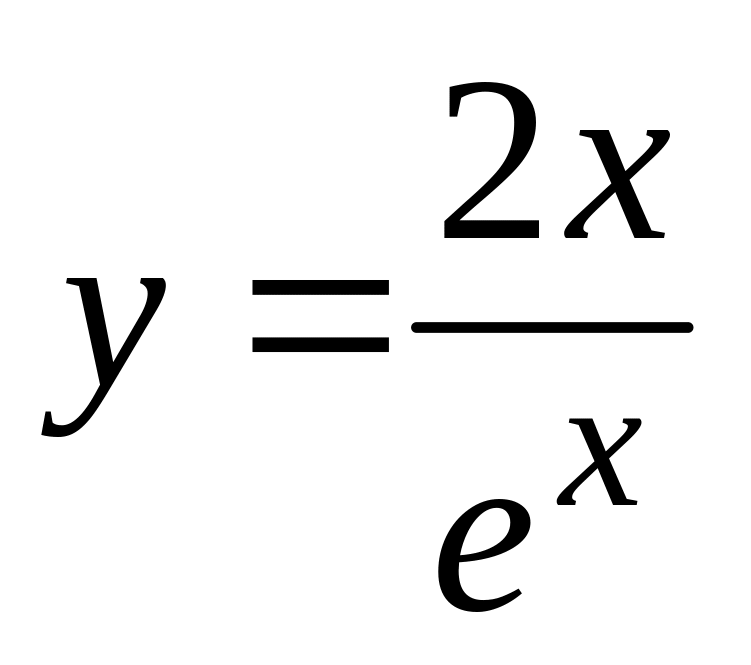 ,
в).
,
в). .
.а).
 ,
б).
,
б).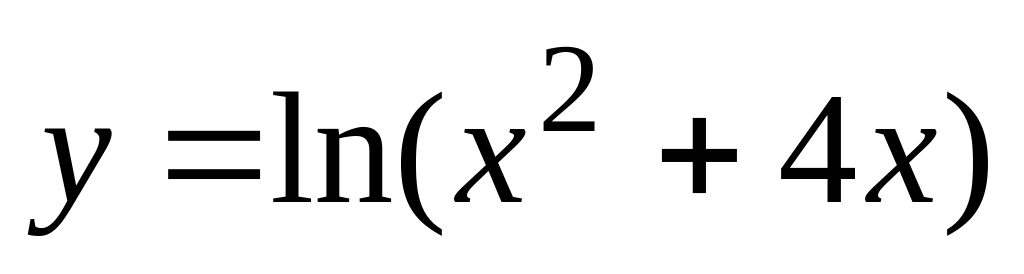 ,
в).
,
в).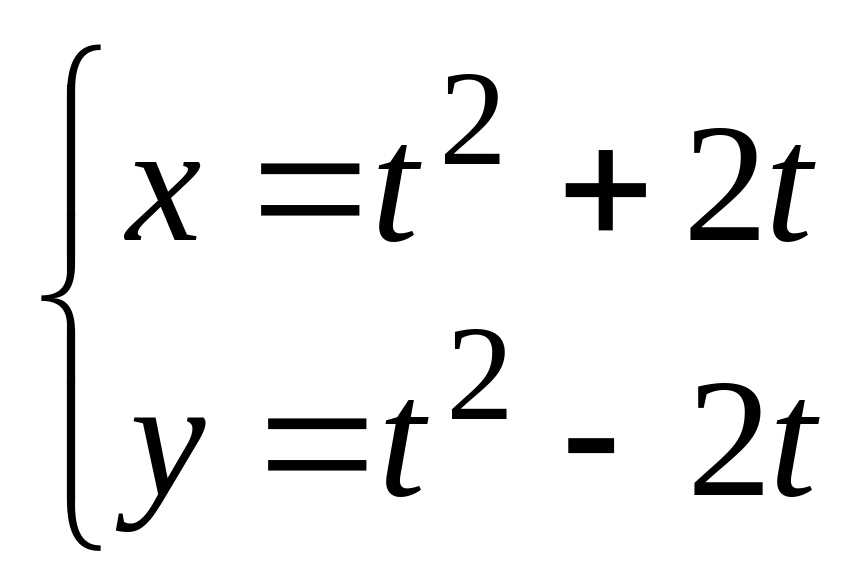 .
.а).
 ,
б).
,
б).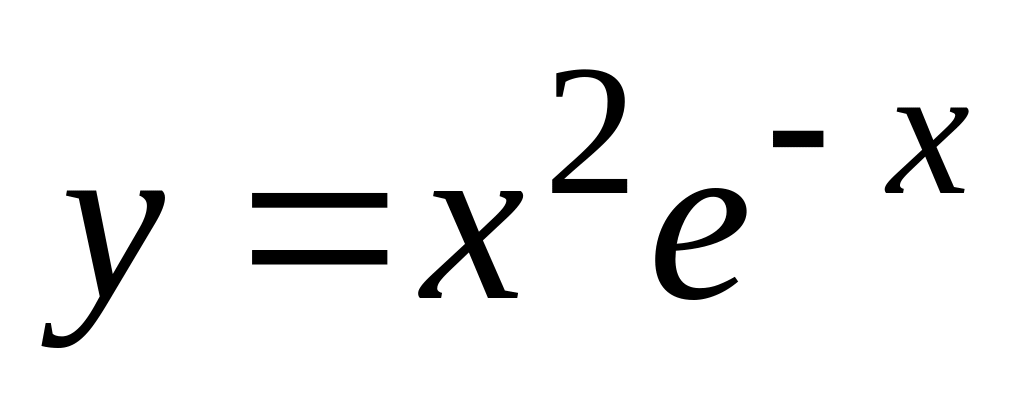 ,
в).
,
в).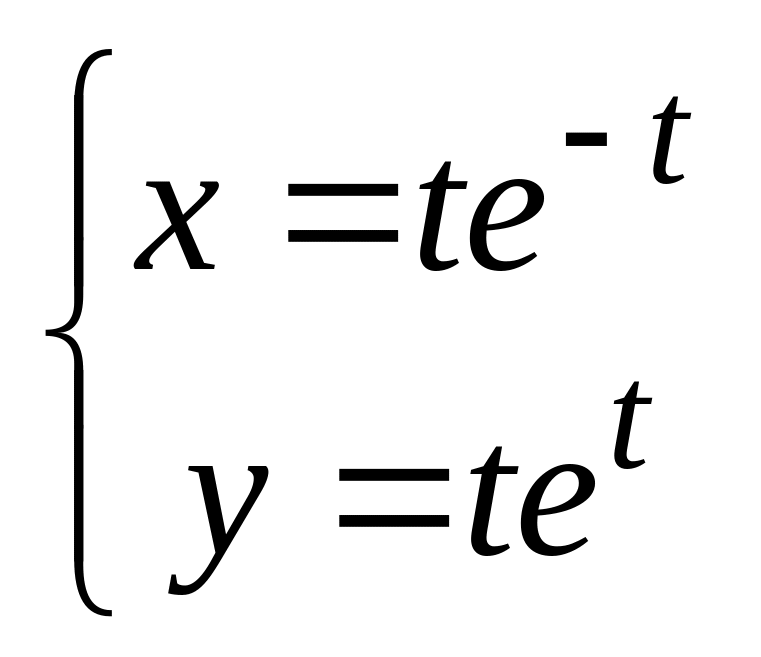 .
.а).
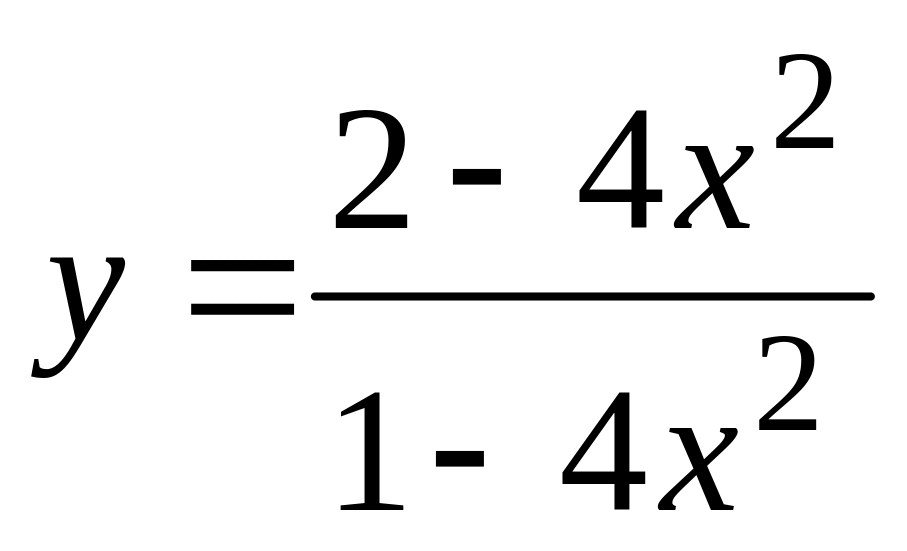 ,
б).
,
в).
,
б).
,
в).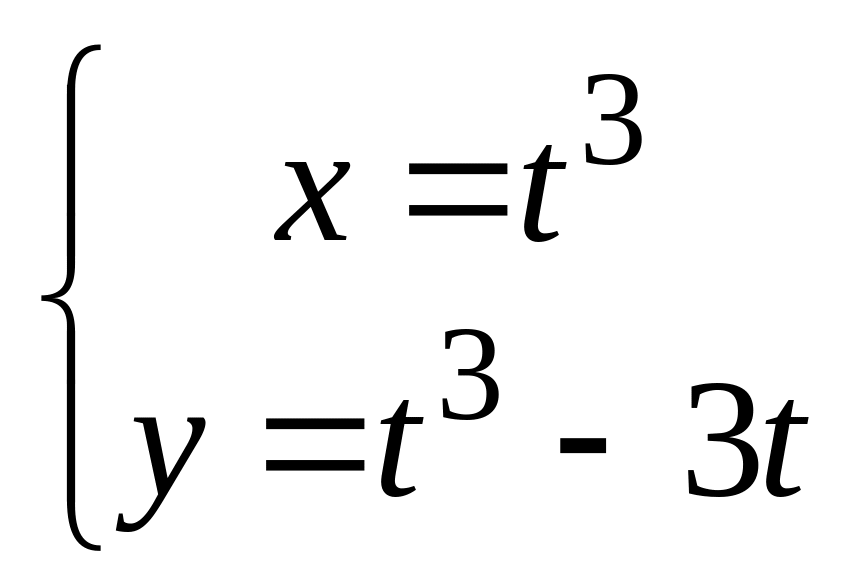 .
.а).
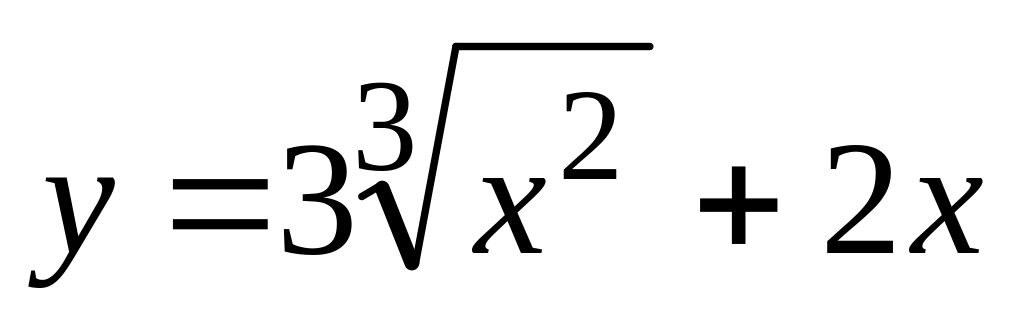 ,
б).
,
б). ,
в).
,
в).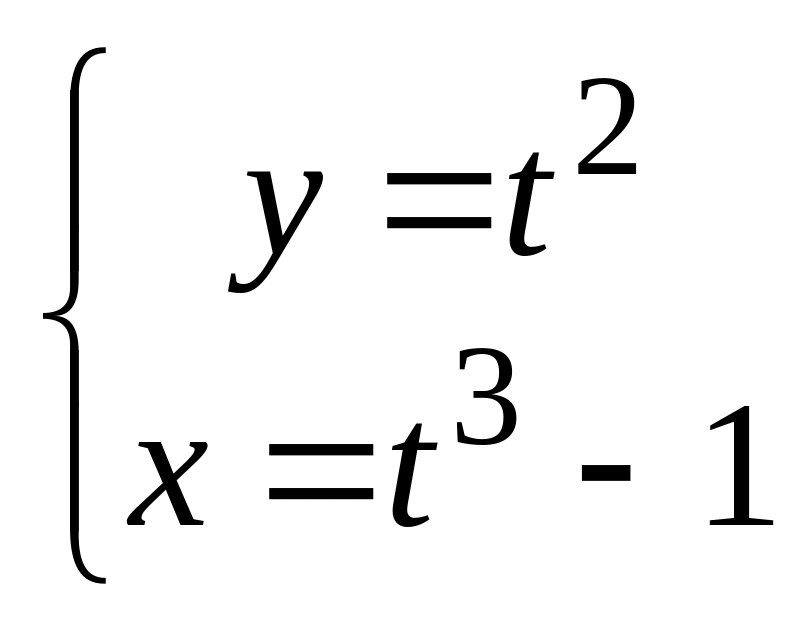 .
.а).
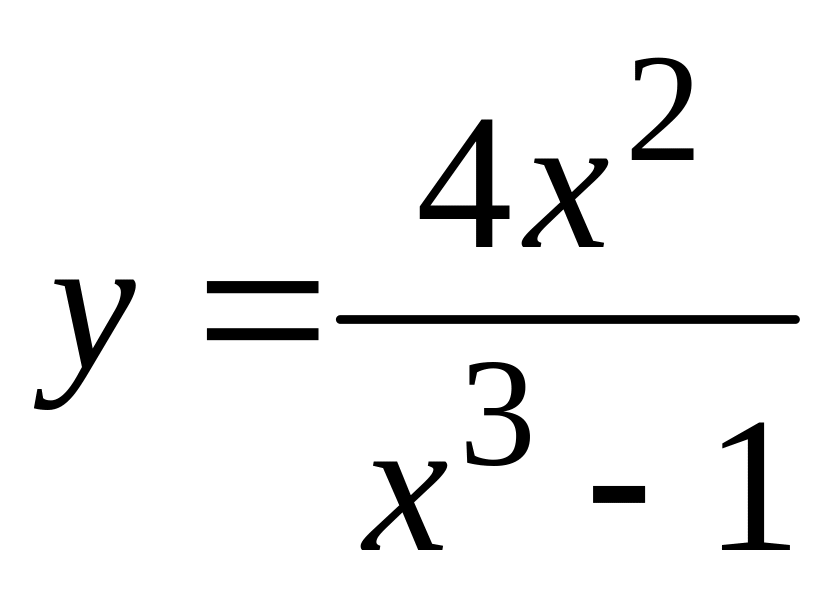 ,
б).
,
б). ,
в).
,
в). .
.а).
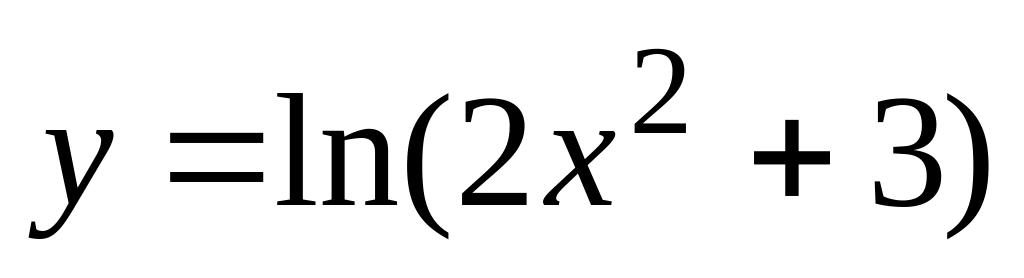 ,
б).
,
б).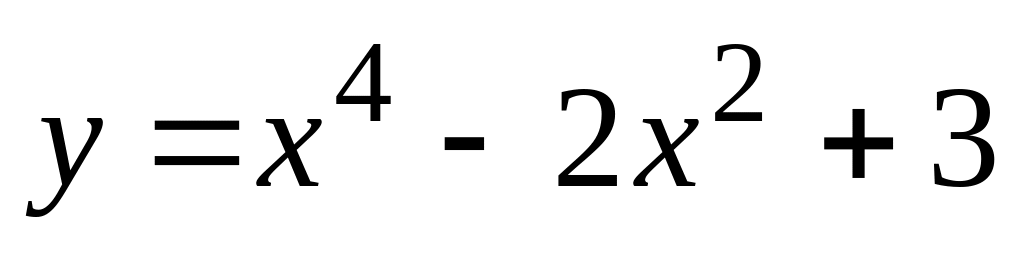 ,
в).
,
в).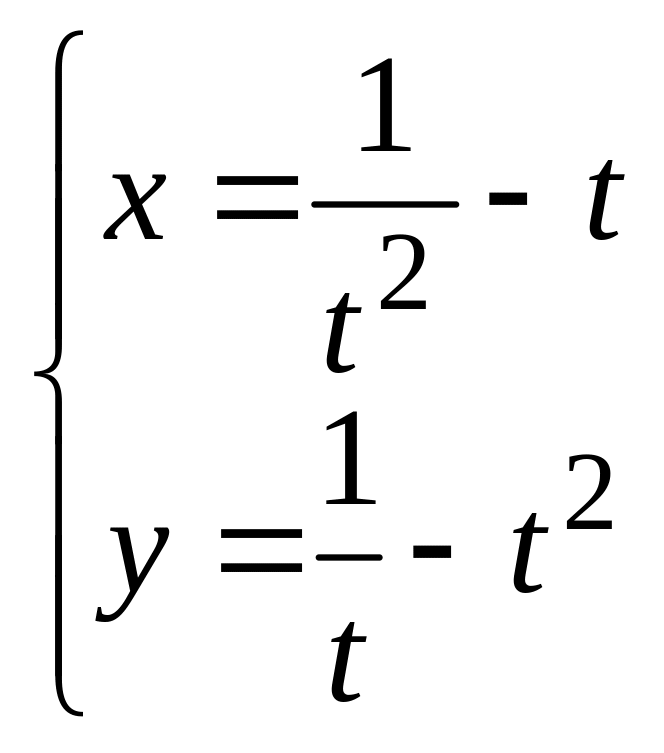 .
.а).
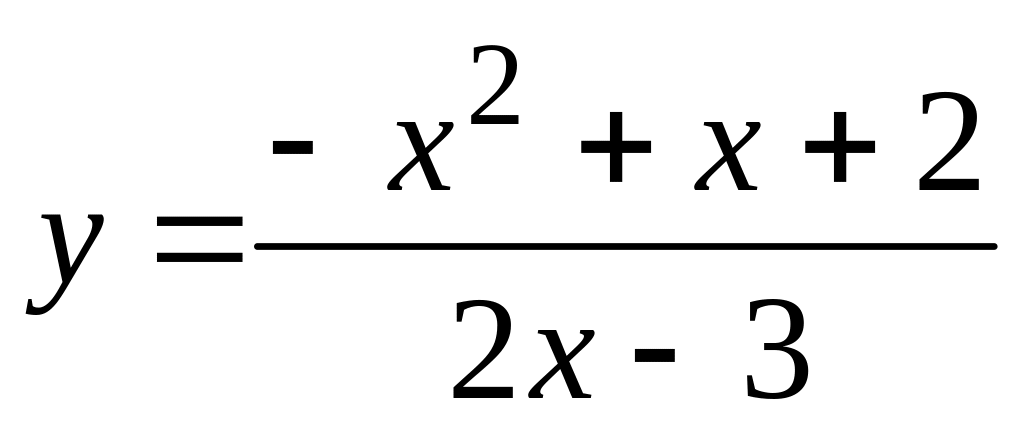 ,
б).
,
б).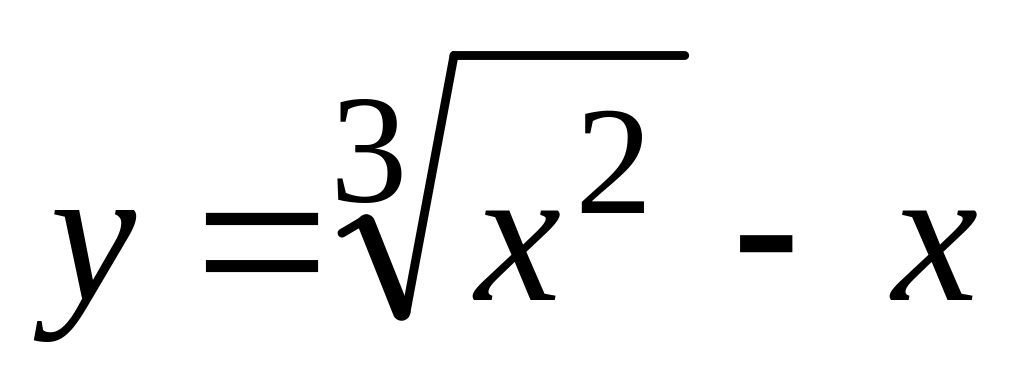 ,
в).
,
в).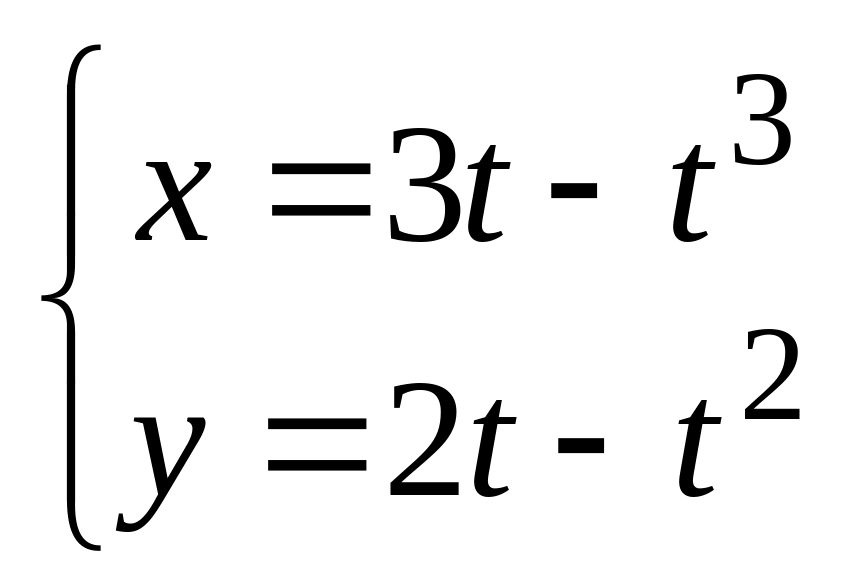 .
.а).
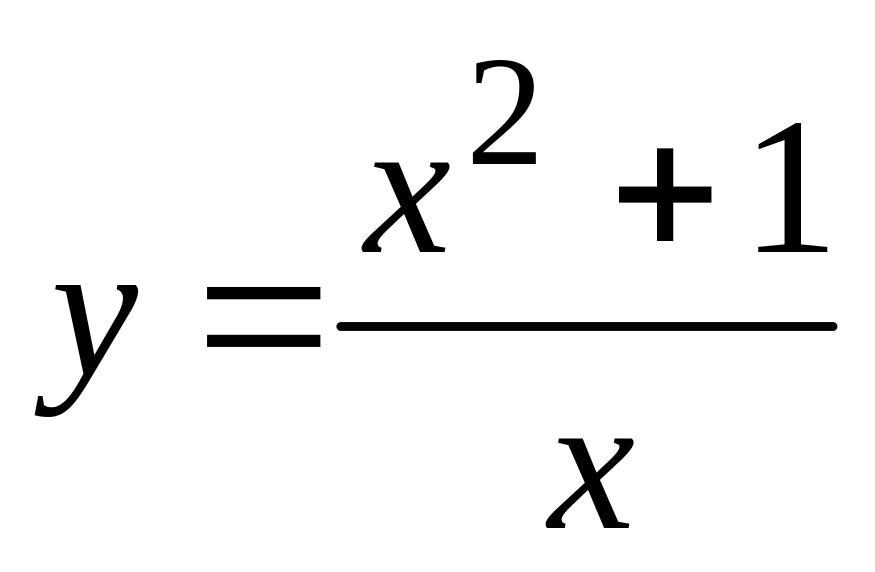 ,
б).
,
б). ,
в).
,
в). .
.а).
 .
б).
.
б).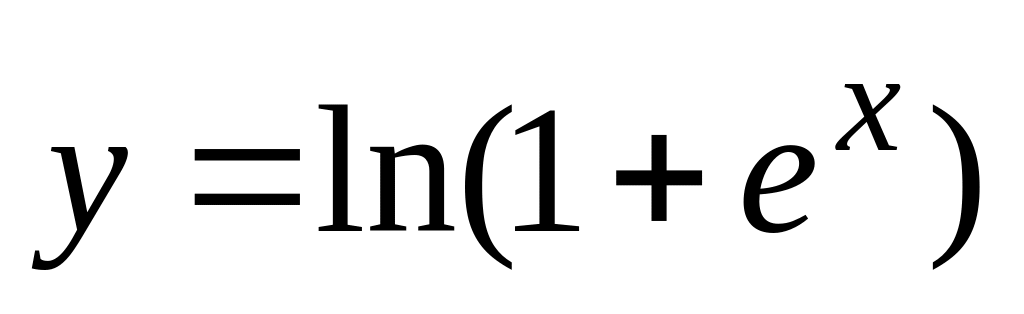 .
в).
.
в).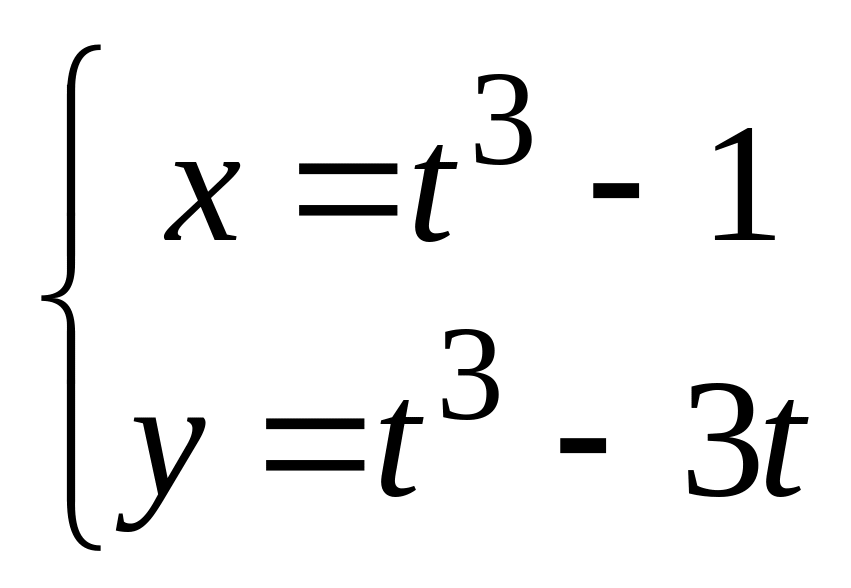 .
.а).
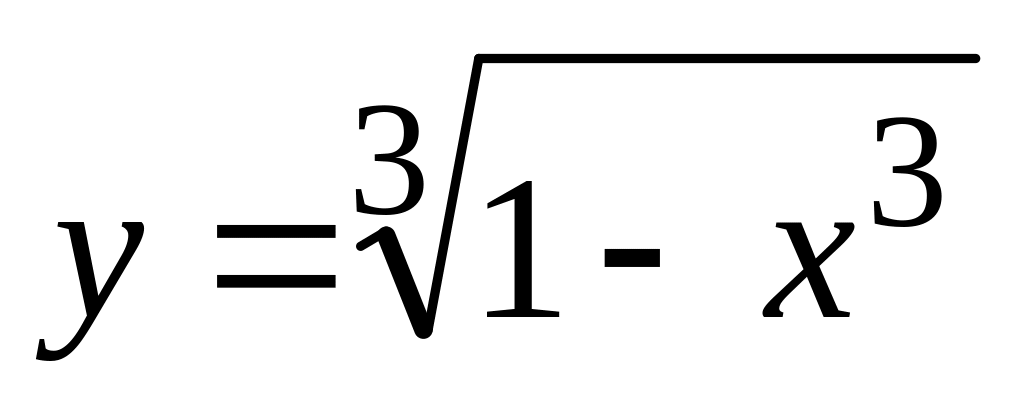 ,
б).
,
б).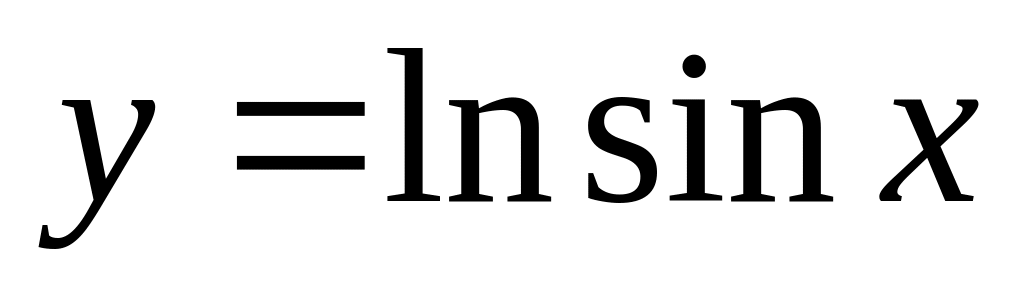 ,
в).
,
в). .
.а).
 ,
б).
,
б). ,
в).
,
в).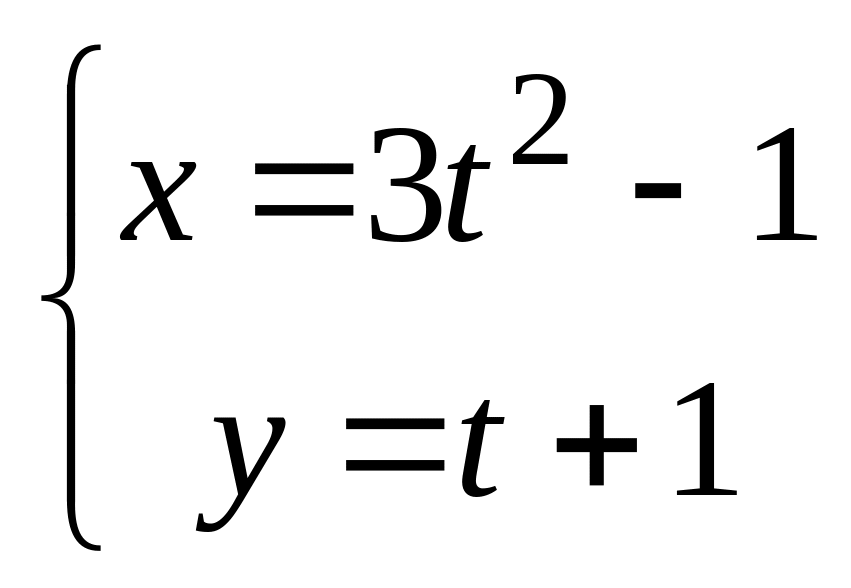 .
.а). . б).
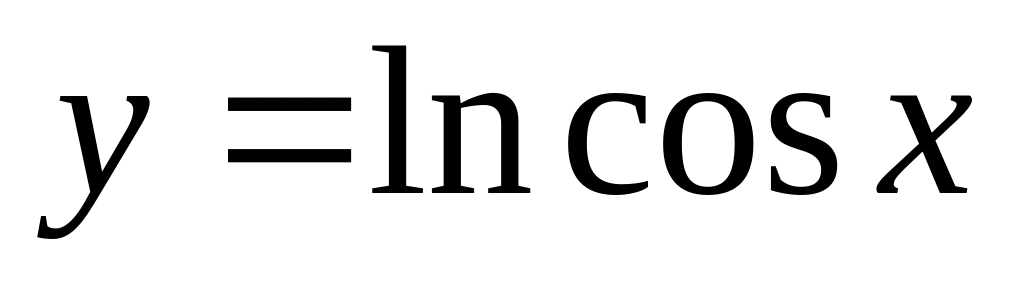 ,
в).
,
в). .
.а).
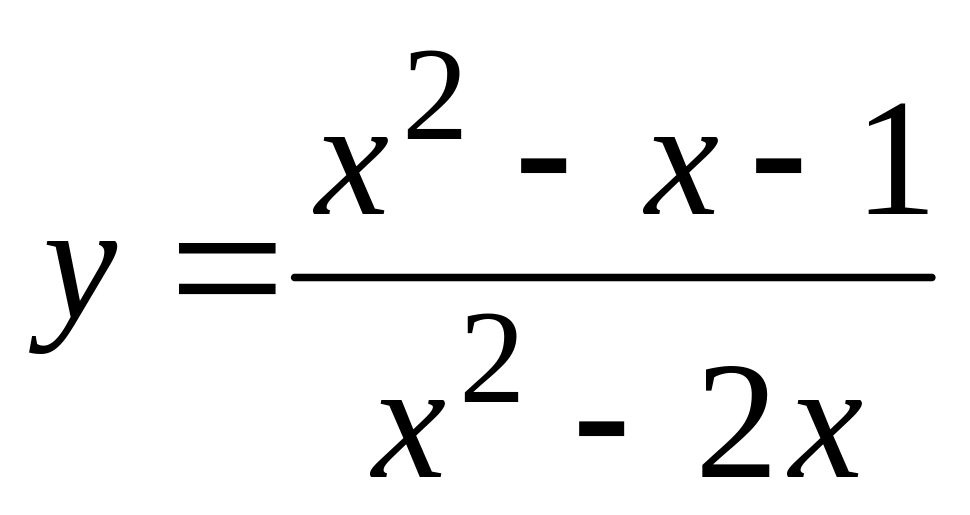 ,
б).
,
в).
,
б).
,
в).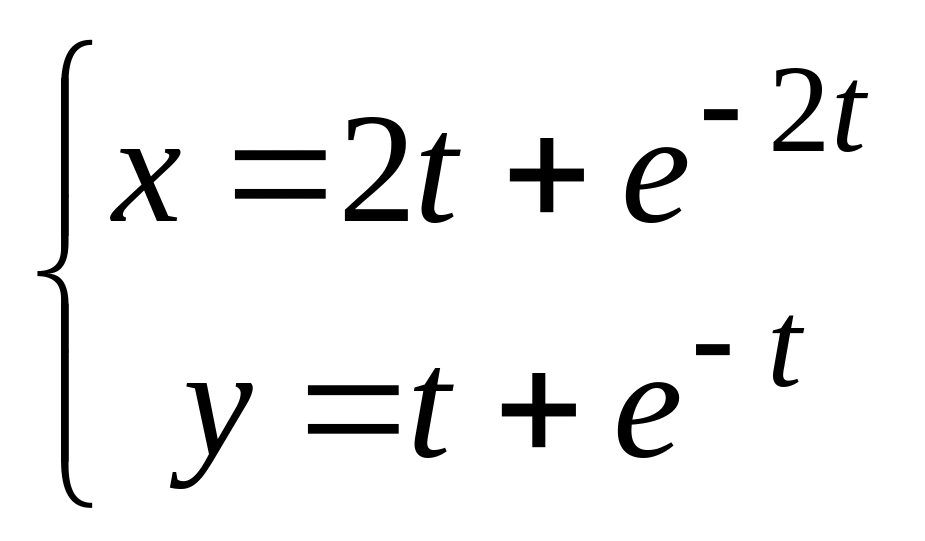 .
.а).
 ,
б).
,
б).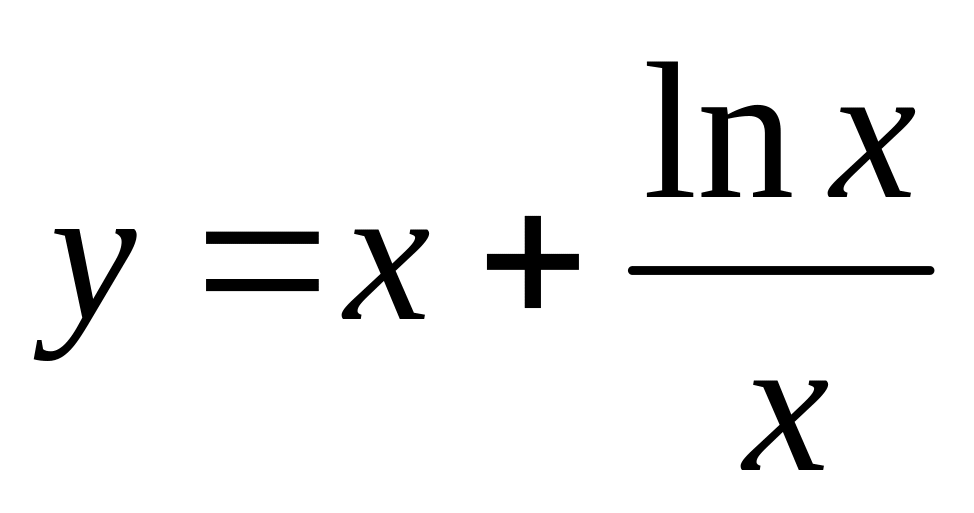 ,
в).
,
в). .
.а).
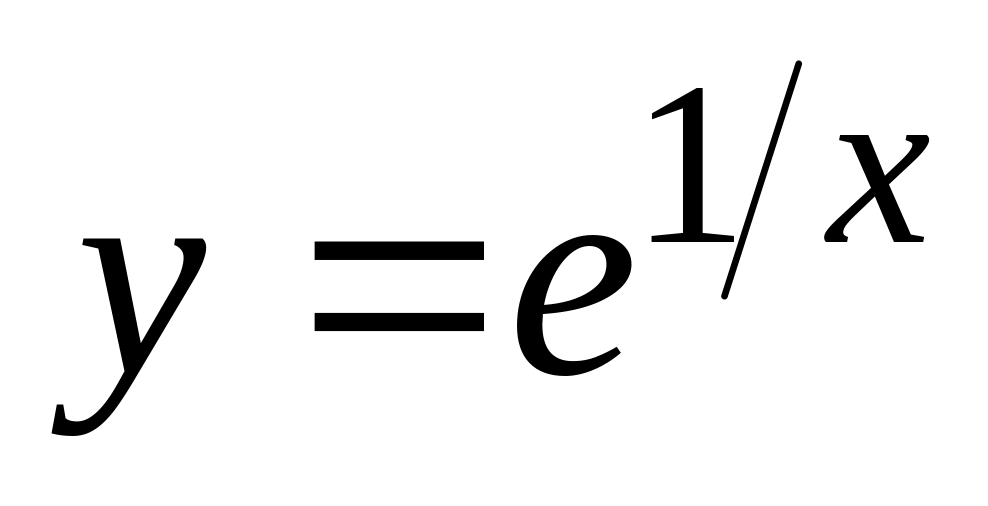 ,
б).
,
б). ,
в).
,
в).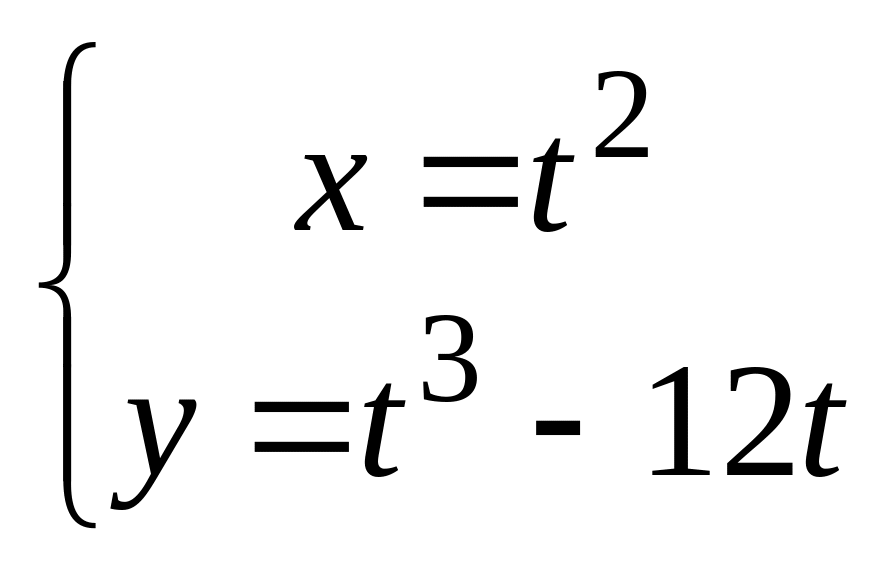 .
.а).
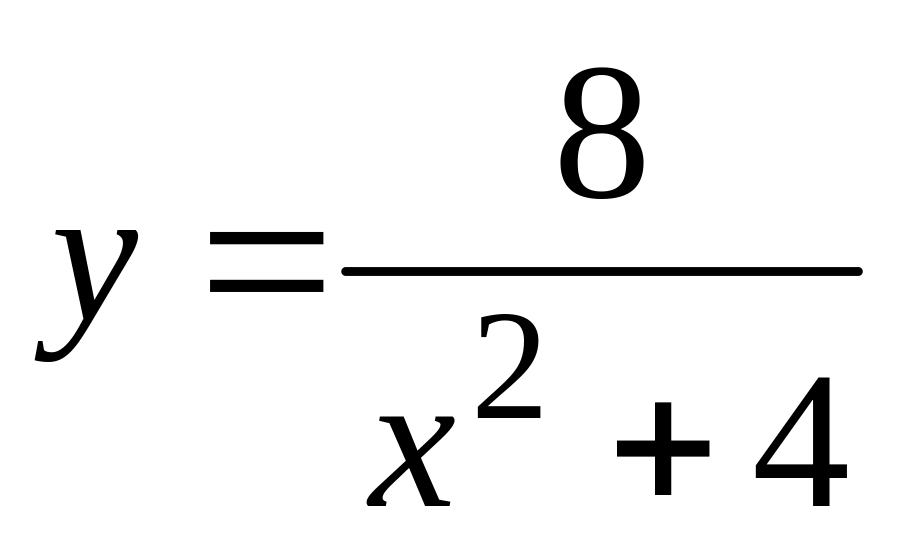 ,
б).
,
б). ,
в).
,
в). .
.а).
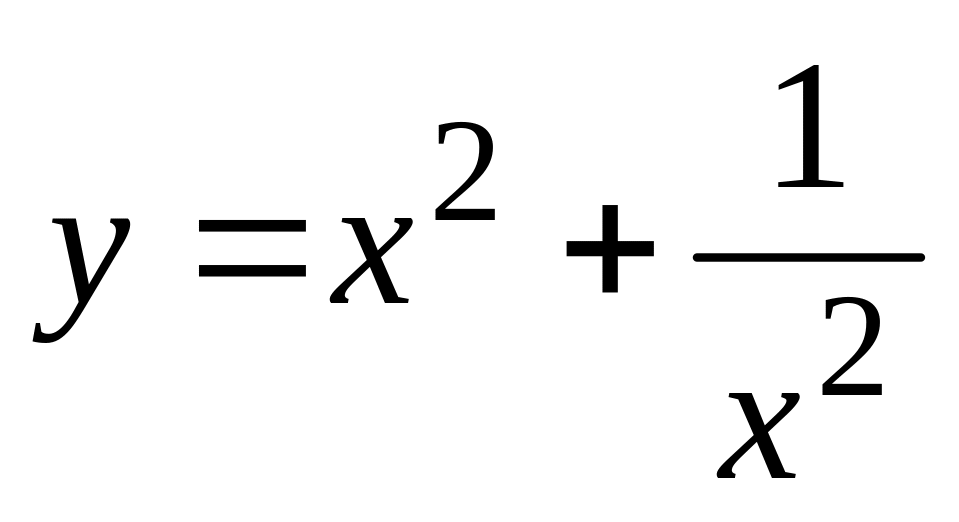 ,
б).
,
б). ,
в).
,
в).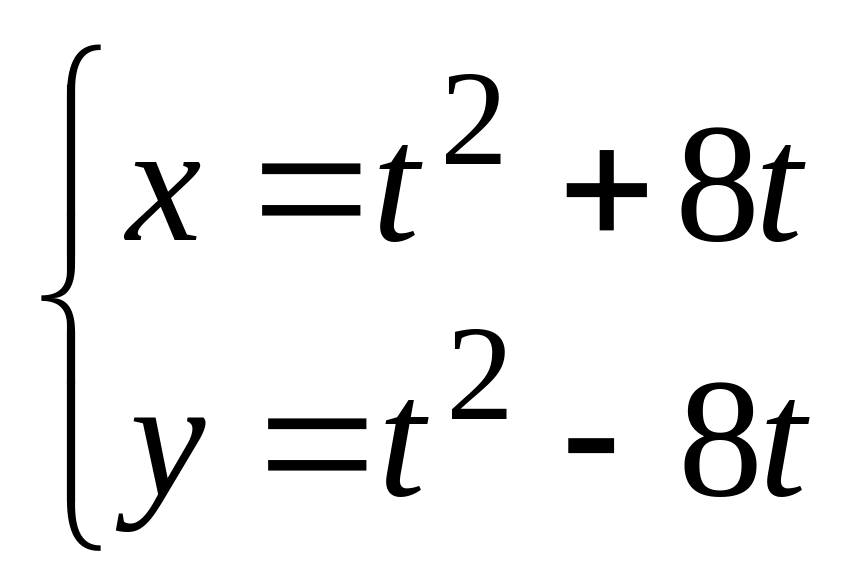 .
.
Задание 2: Решить задачу.
На странице книги печатный текст (вместе с промежутками между строк) должен занимать 216см2. Верхнее и нижнее поля должны быть по 3 см, а правое и левое по 2 см.
Каковы должны быть размеры страницы для того, чтобы ее площадь была наименьшей?
Пренебрегая сопротивлением воздуха, в первом приближении можно считать, что движение вертикально запущенной метеорологической ракеты происходит по закону
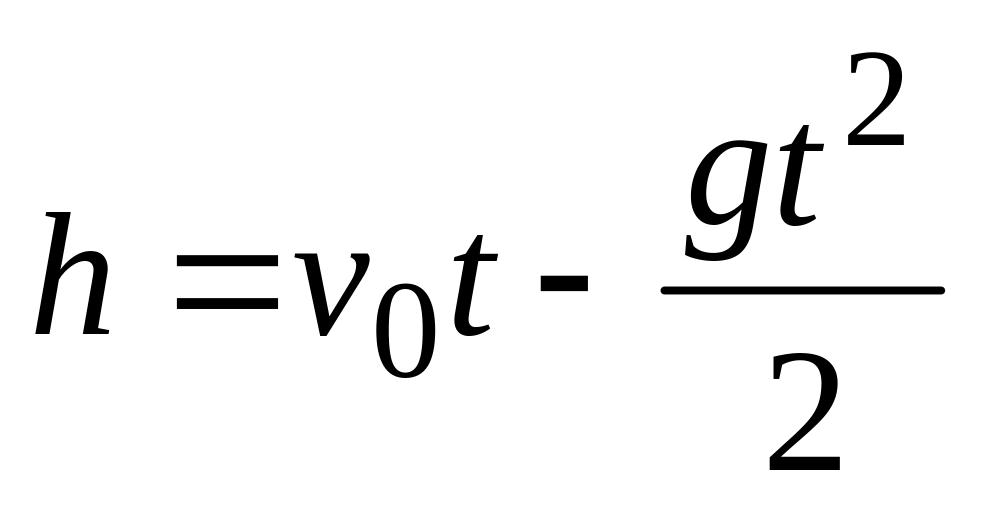 ,
,
 -начальная скорость,
-начальная скорость,
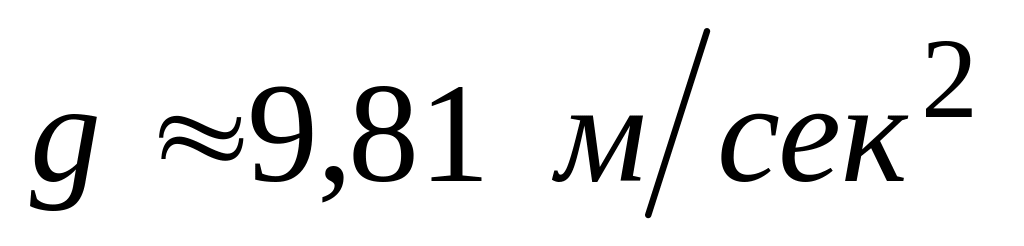 .
Определить какую надо придать ракете
начальную скорость для того, чтобы она
поднялась на высоту
.
Определить какую надо придать ракете
начальную скорость для того, чтобы она
поднялась на высоту

В т. А и В находятся источники света, силы соответственно
 и
и
 .
На отрезке АВ, равном «а» найти наименее
освещенную точку М (освещенность точки
обратно пропорциональна к квадрату
расстояния ее от источника света:
.
На отрезке АВ, равном «а» найти наименее
освещенную точку М (освещенность точки
обратно пропорциональна к квадрату
расстояния ее от источника света:
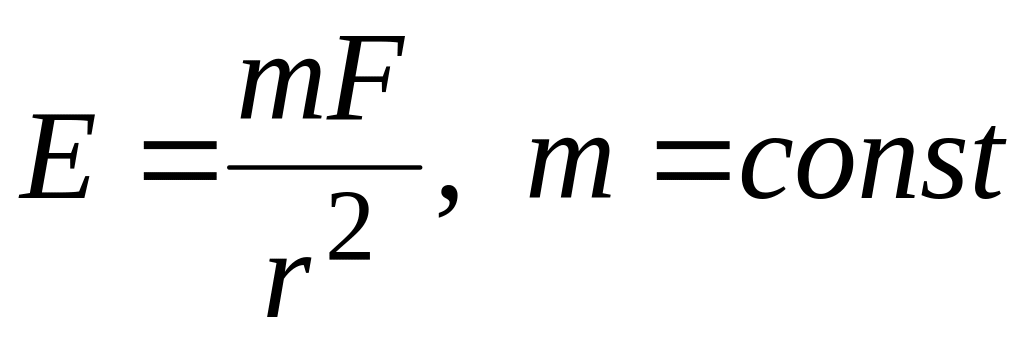 ).
).
Полоса жести шириной «а» должна быть согнута в виде открытого желоба, так, чтобы поперечное сечение желоба имело форму кругового сегмента. Каким должен быть центральный угол, опирающийся на этот сегмент для того, чтобы вместимость желоба была наибольшей?
Через точку (3;5) провести прямую с отрицательным угловым коэффициентом так, чтобы площадь треугольника, образованного этой прямой и осями координат, была наименьшей?
Сосуд, состоящий из цилиндра, заканчивающийся снизу полусферой, должен вмещать 18 л. воды. Найти размеры сосуда, при которых на его изготовление пойдет наименьшее количество материала.
Найти радиус основания и высоту конуса наименьшего объема, описанного около шара радиуса R.
При каких линейных размерах закрытая цилиндрическая банка данной вместимости будет иметь наименьшую полную поверхность?
Найти радиус основания и высоту цилиндра с наибольшей боковой поверхностью, который можно вписать в шар радиуса R.
Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R.
Каковы должны быть коэффициенты
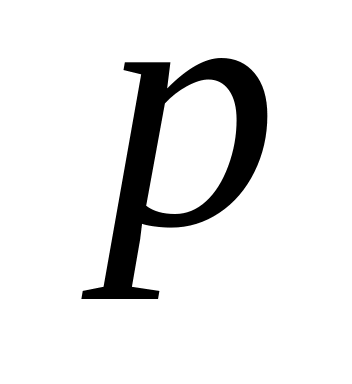 и
и
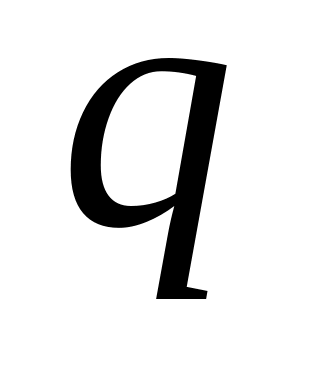 трехчлена
трехчлена
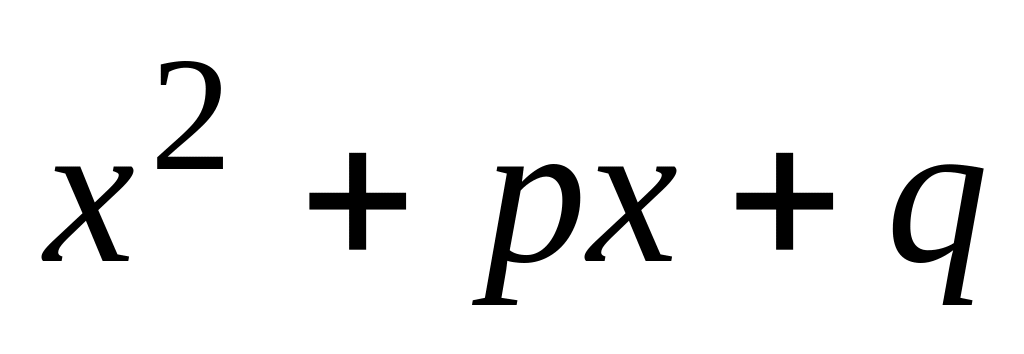 ,
чтобы этот трехчлен при
,
чтобы этот трехчлен при
 имел минимум, равный
имел минимум, равный
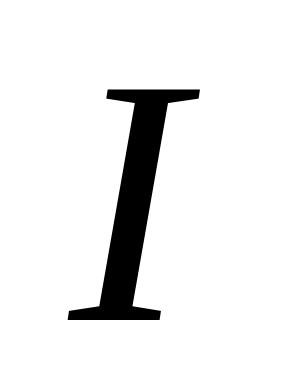 ?
?
Лампа висит над центром круглого стола радиуса R. При какой высоте лампы над столом освещенность предмета, лежащего на краю стола, будет наилучшая? (Освещенность прямо пропорциональна косинусу угла падения лучей света и обратно пропорциональна квадрату расстояния от источника).

Через точку А (2;1) провести прямую с отрицательным угловым коэффициентом так, чтобы сумма длин отрезков, отсекаемых ею на осях координат, была наименьшей.
Проволокой длиной 20м требуется огородить клумбу, которая должна иметь форму кругового сектора. Какой следует взять радиус круга, чтобы площадь клумбы была наибольшей?
Требуется поставить палатку данного объема V имеющего форму прямого кругового конуса. Найти отношение высоты конуса к радиусу его основания, при котором на палатку уйдет наименьшее количество материала.
Энергия, затрачиваемая в единицу времени на движение парохода, пропорциональна кубу скорости парохода, развиваемой им в стоячей воде. Найти наиболее экономичную скорость движения парохода, если требуется пройти определенное расстояние против течения, скорость которого составляет 6 км./ч.
Требуется из жести изготовить ведро данного объема V цилиндрической формы без крышки. Найти высоту цилиндра и радиус его основания, при котором на ведро уйдет наименьшее количество материала.
Дождевая капля, начальная масса которой равна
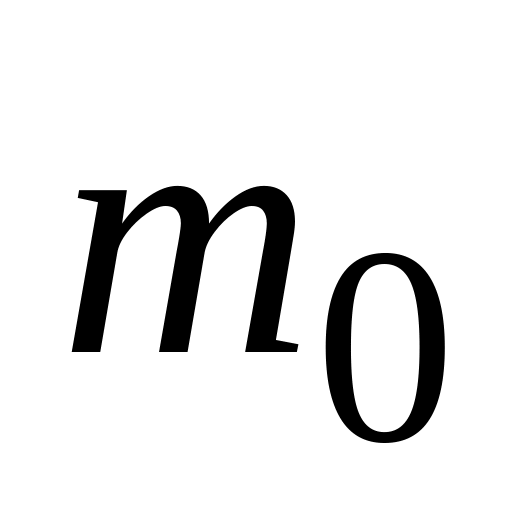 ,
падает под действием силы тяжести
равномерно испаряясь, так что убыль
массы пропорциональна времени
(коэффициент пропорциональности равен
К). Найти, через сколько секунд после
начала падения кинетическая энергия
капли будет наибольшей. При решении
задачи сопротивлением воздуха
пренебречь.
,
падает под действием силы тяжести
равномерно испаряясь, так что убыль
массы пропорциональна времени
(коэффициент пропорциональности равен
К). Найти, через сколько секунд после
начала падения кинетическая энергия
капли будет наибольшей. При решении
задачи сопротивлением воздуха
пренебречь.
Найти стороны прямоугольника наибольшей площади, который можно вписать в эллипс с осями
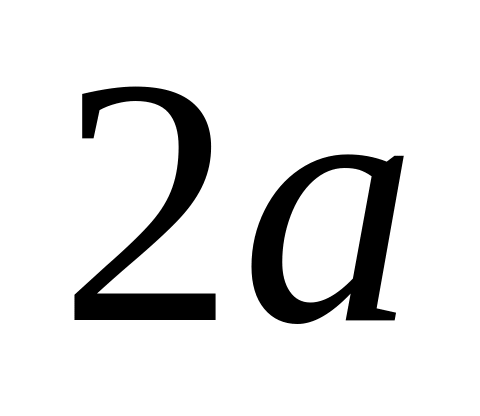 и
и
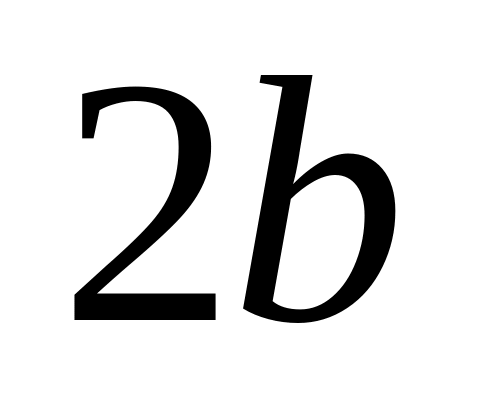 .
.
Из круглого бревна диаметра Д требуется вырезать балку прямоугольного сечения. Каковы должны быть ширина и высота этого сечения, чтобы балка оказывала наибольшее сопротивление на изгиб (сопротивление балки на изгиб пропорционально произведению ширины ее поперечного сечения на квадрат его стороны:
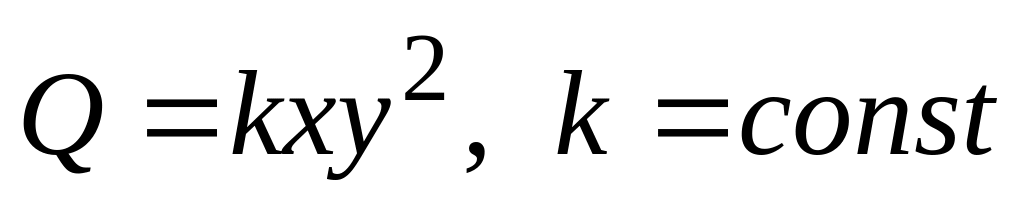 )?
)?
Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна 300 см. При каких размерах сторон прямоугольника окно будет пропускать наибольшее количество света?
Через какую точку эллипса
 следует
провести касательную, чтобы площадь
треугольника, составленного этой
касательной и осями координат, была
наименьшей.
следует
провести касательную, чтобы площадь
треугольника, составленного этой
касательной и осями координат, была
наименьшей.
Периметр равнобедренного треугольника равен 2р. Каковы должны быть его стороны, чтобы объем конуса, образованного вращением этого треугольника вокруг своей высоты, был наибольшим?
Периметр равнобедренного треугольника равен 2р. Каковы должны быть его стороны, чтобы объем тела образованного вращением этого треугольника вокруг его основания, был наибольшим?
Из круга вырезан сектор с центральным углом
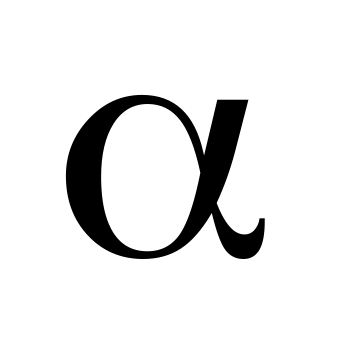 .
Из сектора свернута коническая
поверхность. При каком значении угла
объем полученного конуса будет
наибольшим?
.
Из сектора свернута коническая
поверхность. При каком значении угла
объем полученного конуса будет
наибольшим?
Требуется изготовить ящик с крышкой, объем которого был бы 72 см3, причем стороны основания относились бы как 1:2. Каковы должны быть размеры всех сторон, чтобы полная поверхность была наименьшей?
Кровельщик желает сделать открытый желоб наибольшей вместимости, у которого дно и бока были бы по 10 см и бока были бы одинаково наклонены ко дну. Какова должна быть ширина желоба наверху?
Сосуд с вертикальной стенкой высоты
 стоит на горизонтальной плоскости.
Определить положение отверстия, при
котором дальность струи будет наибольшая,
если скорость вытекающей жидкости по
закону Торричелли равна
стоит на горизонтальной плоскости.
Определить положение отверстия, при
котором дальность струи будет наибольшая,
если скорость вытекающей жидкости по
закону Торричелли равна
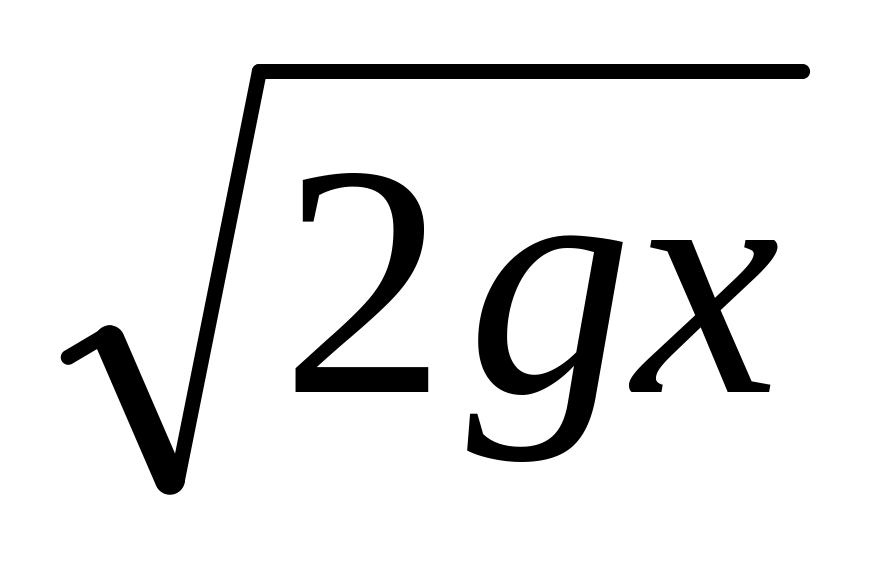 ,
где
,
где
 - глубина расположения отверстия, а
- глубина расположения отверстия, а
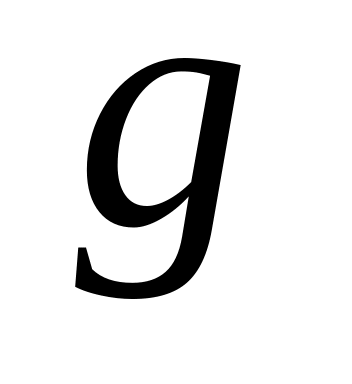 - ускорение свободного падения.
- ускорение свободного падения.
На параболе
 найти точку, ближайшую к точке (3;0).
найти точку, ближайшую к точке (3;0).
Открытый жестяной бак с квадратным основанием должен вмещать V литров. При каких размерах на изготовление бака потребуется наименьшее количество жести?
Задание 3: Найти наибольшее и наименьшее значение функции на отрезке.
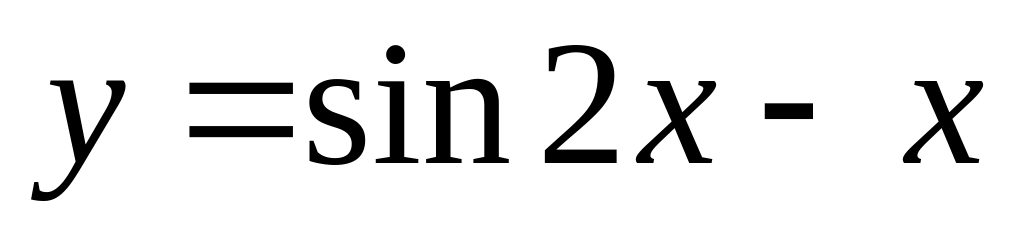 ,
,
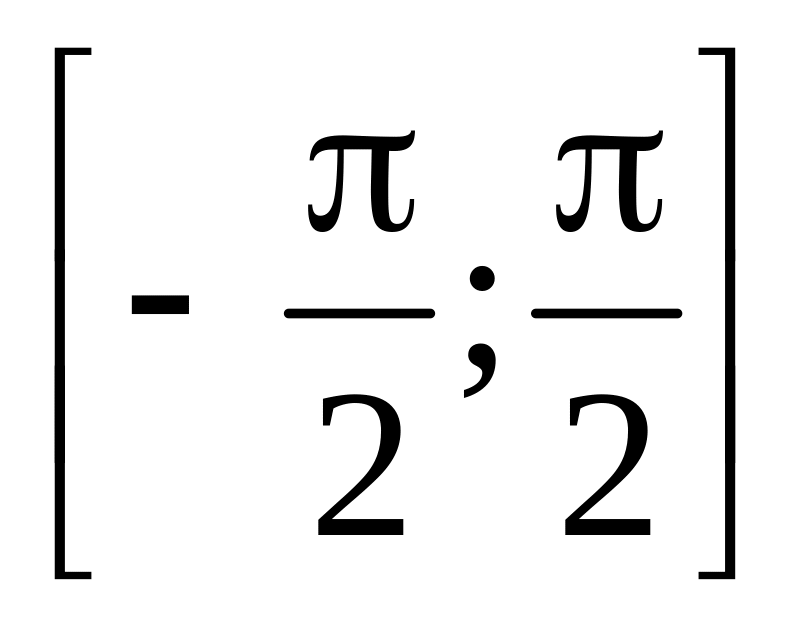 .
.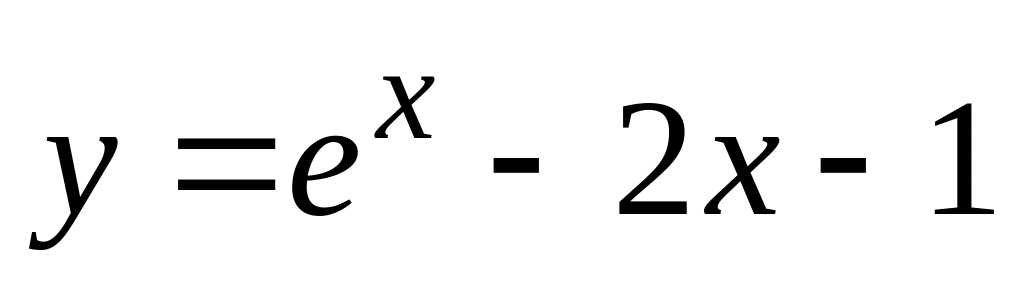 ,
,
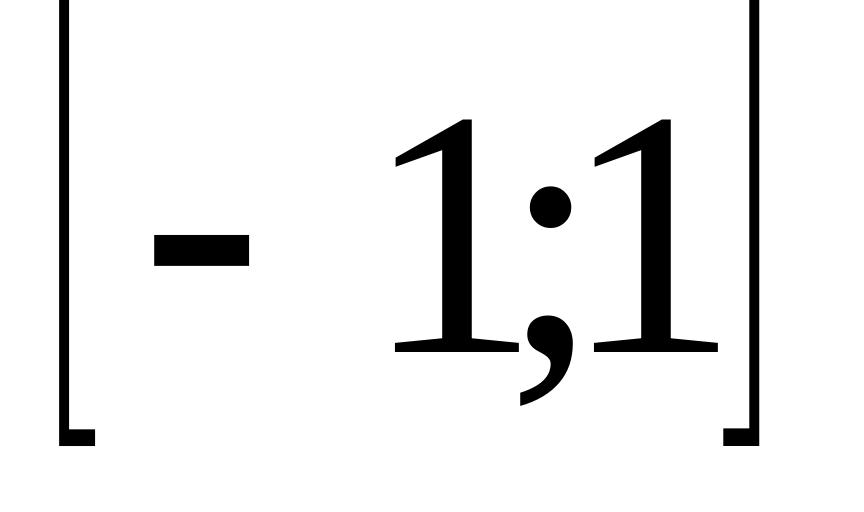 .
.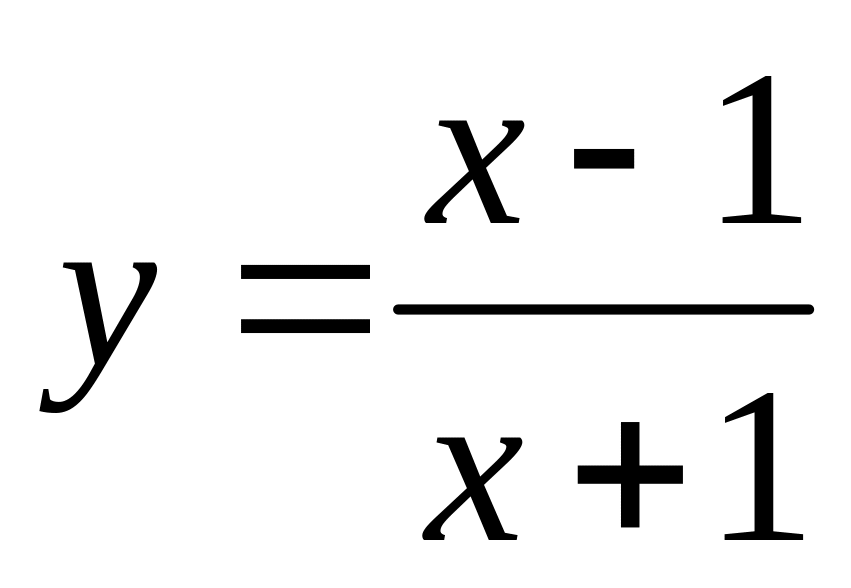 ,
,
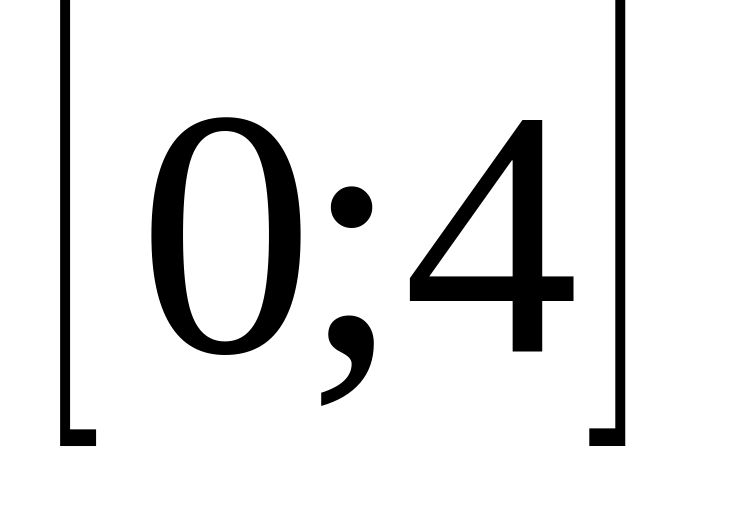 .
.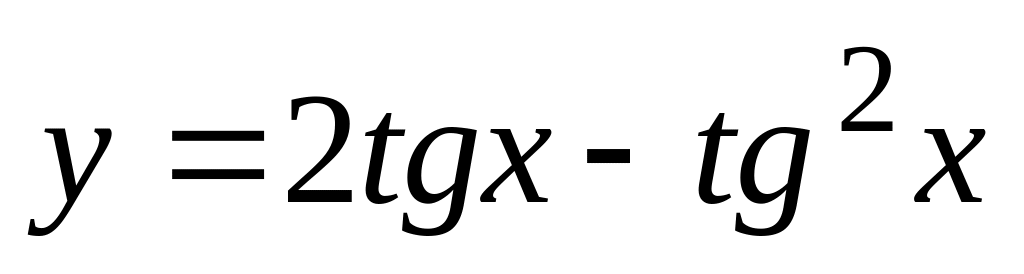 ,
,
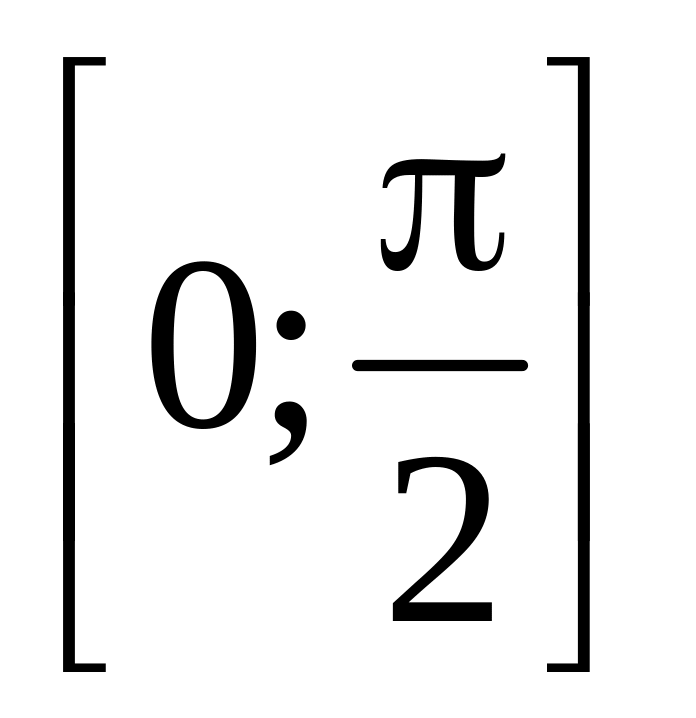 .
.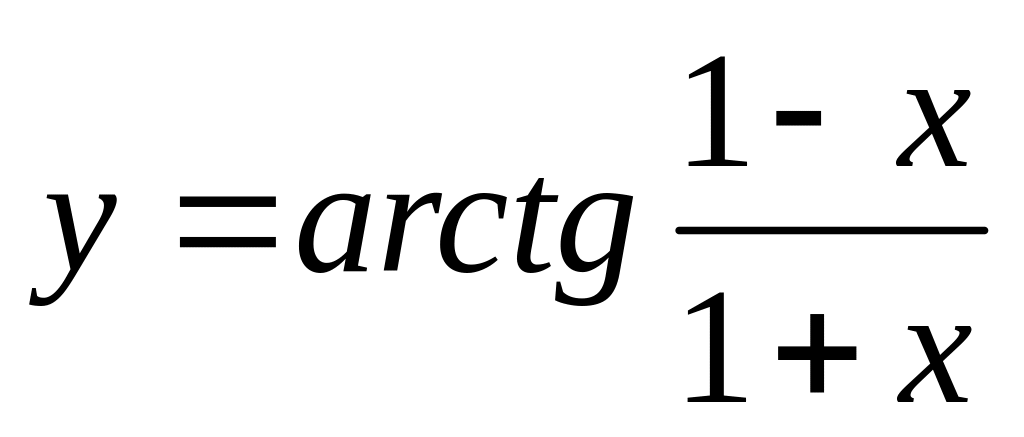 ,
,
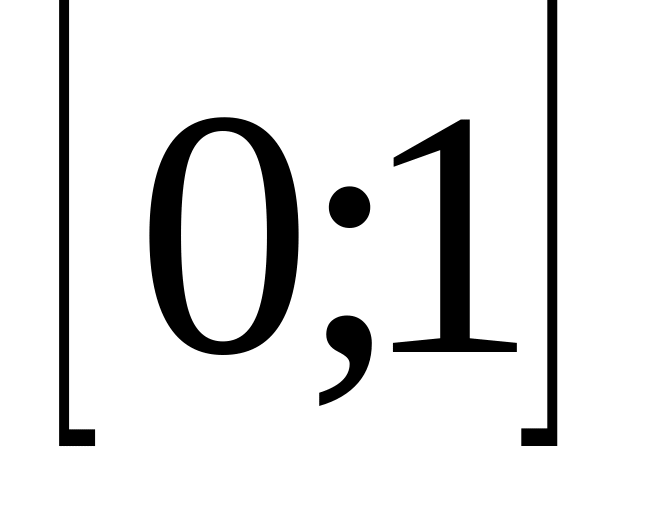 .
.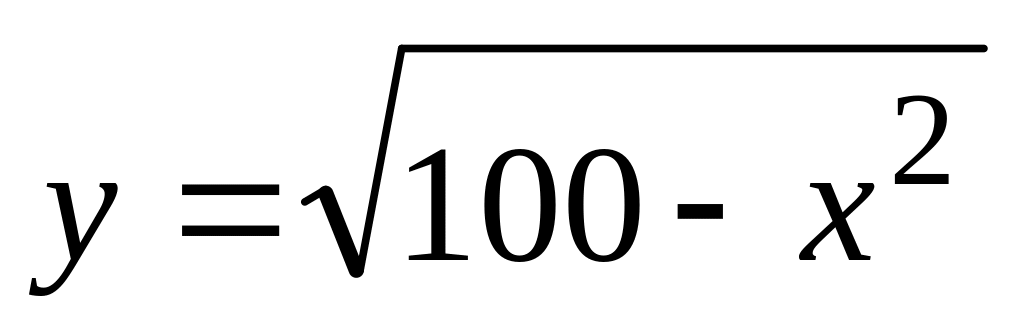 ,
,
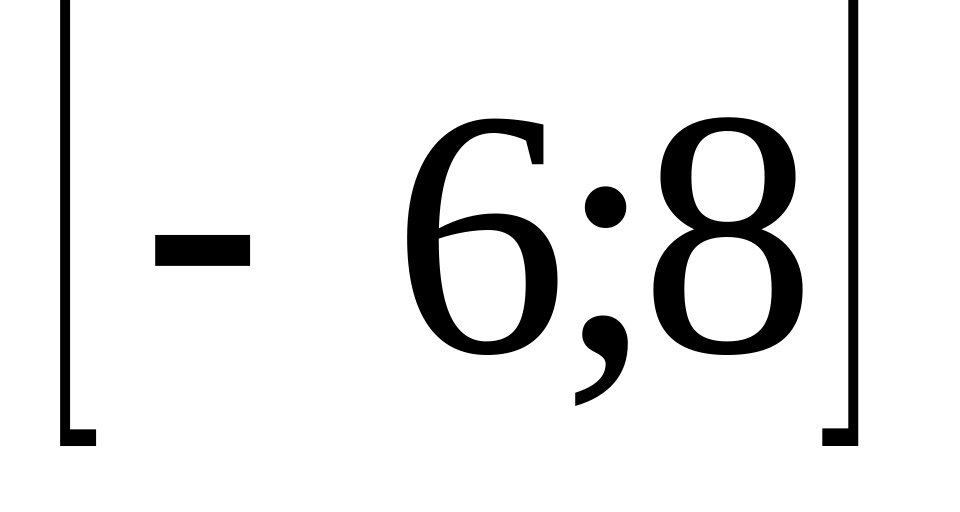 .
.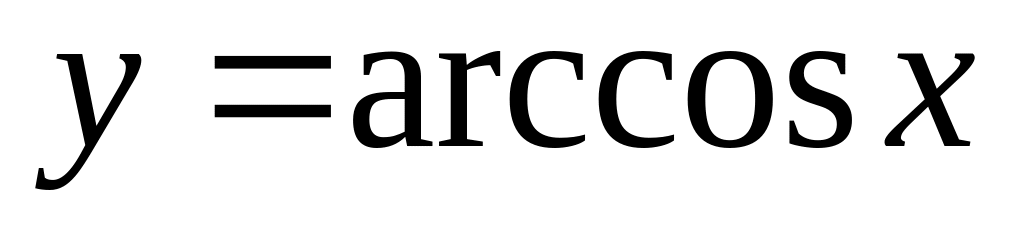 ,
во всей области существования.
,
во всей области существования.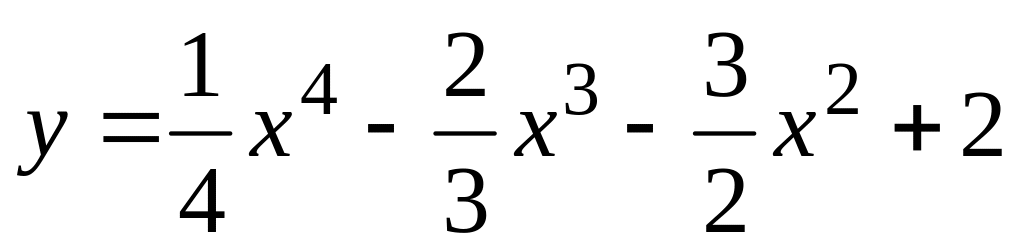 ,
,
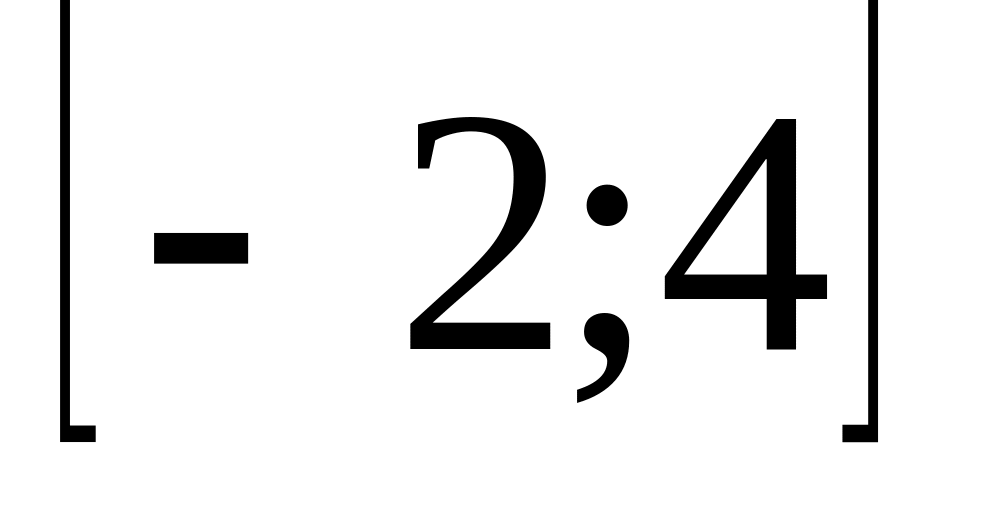 .
.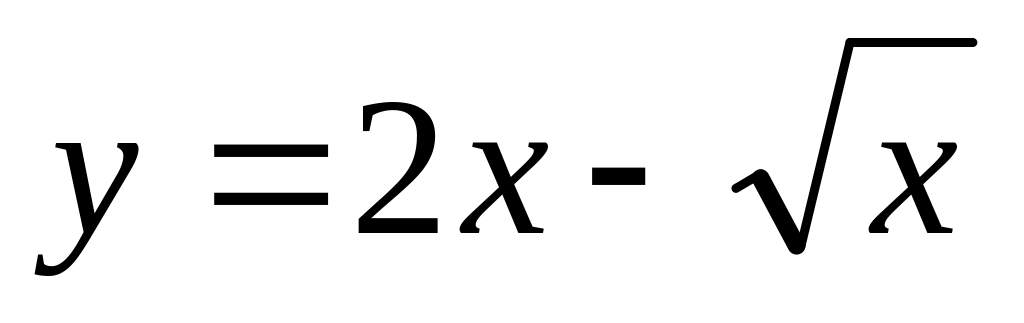 ,
.
,
. ,
,
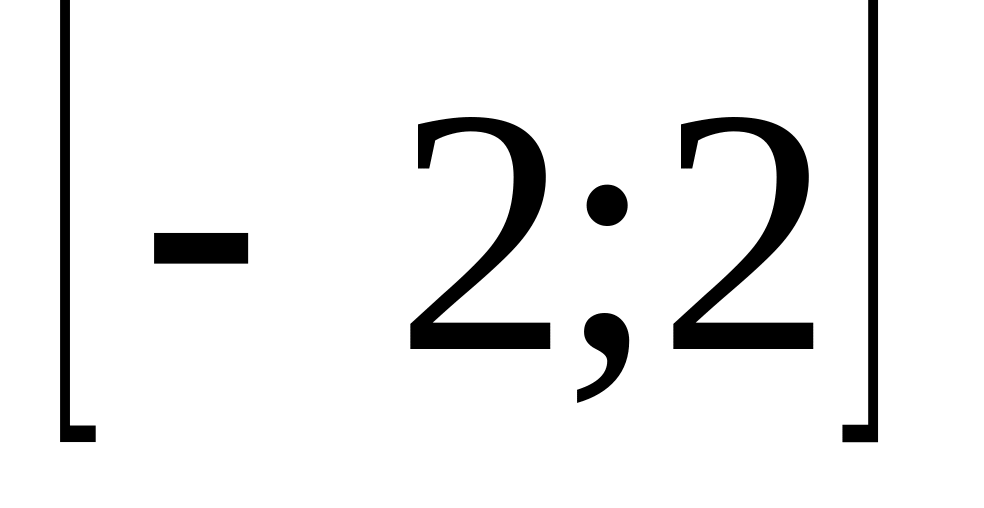 .
.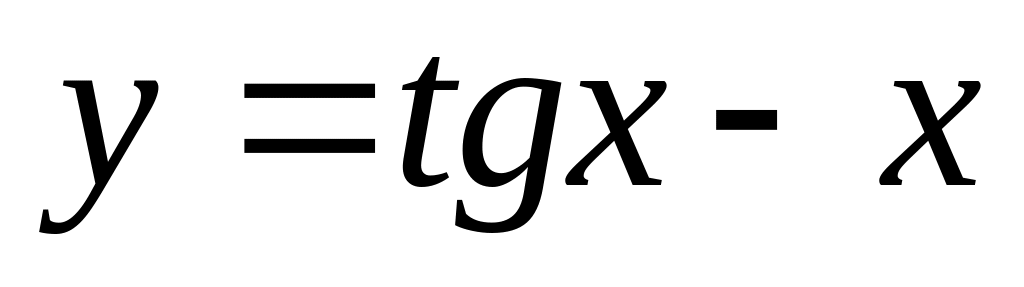 ,
,
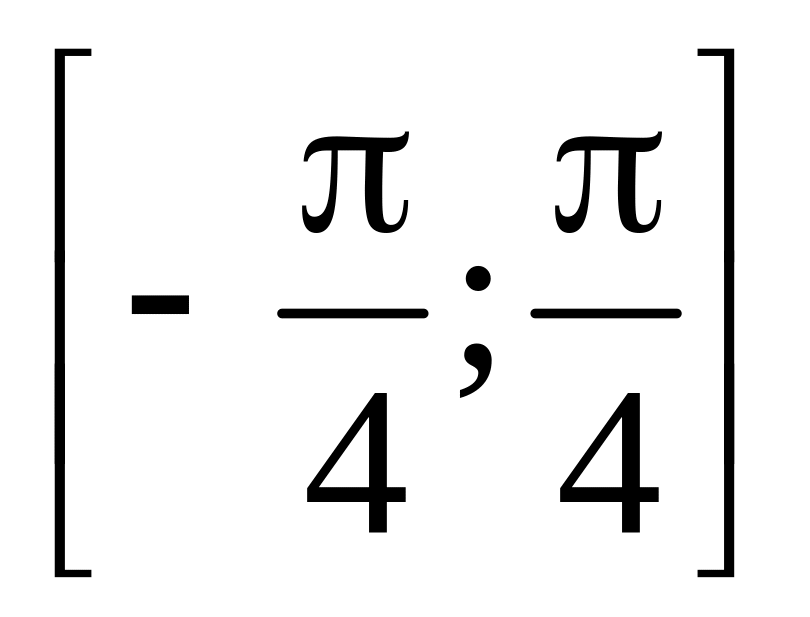 .
. ,
,
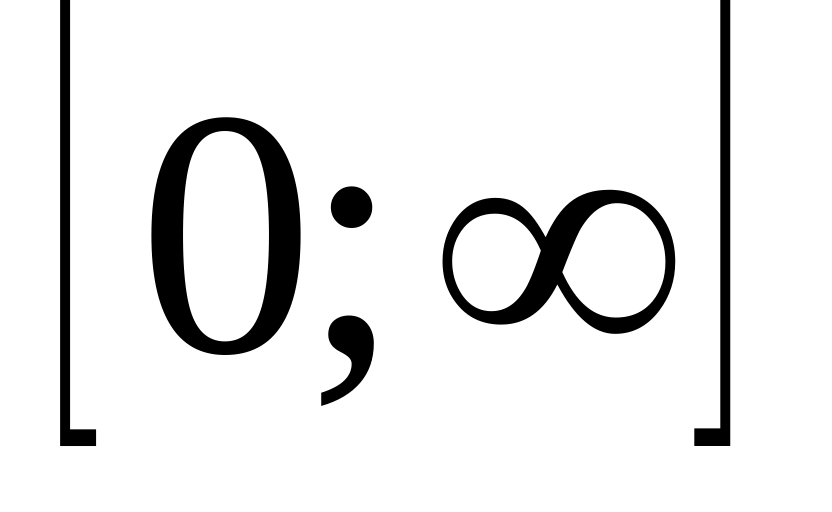 .
.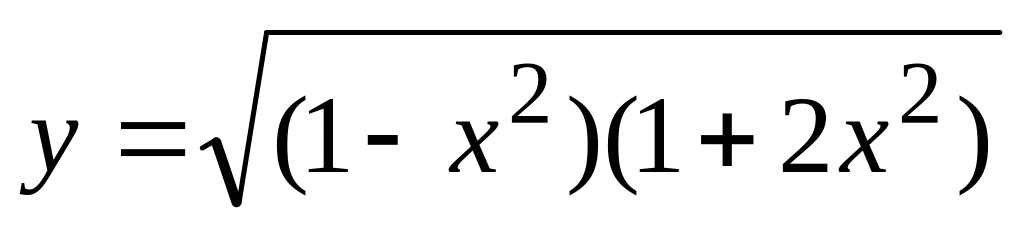 ,
,
 .
. ,
,
 .
.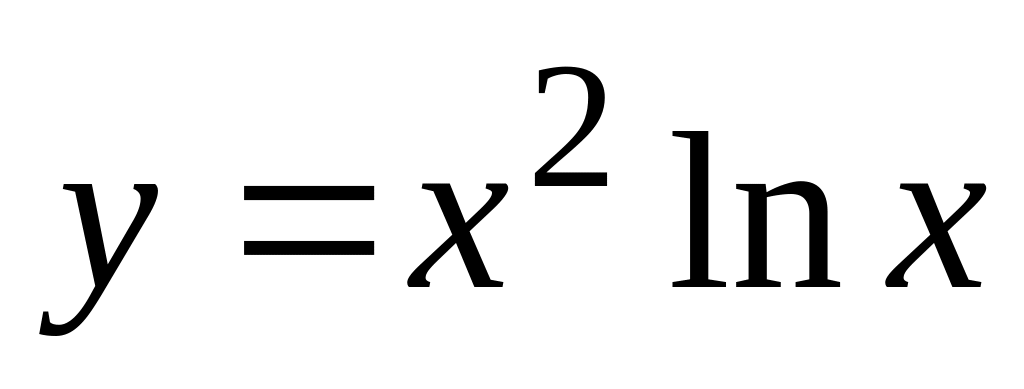 ,
,
 .
.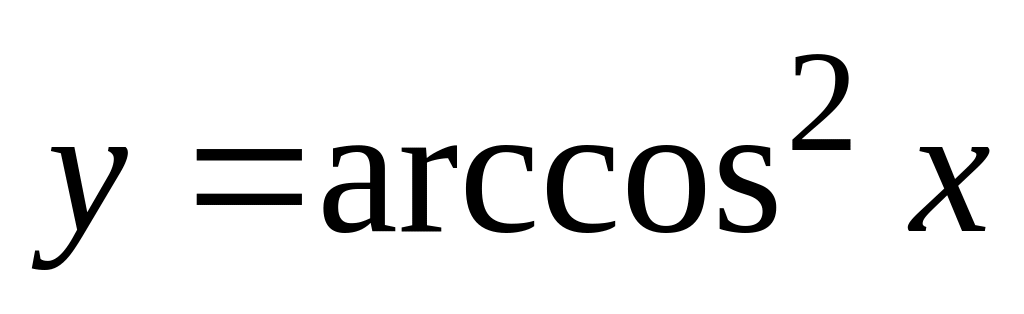 ,
,
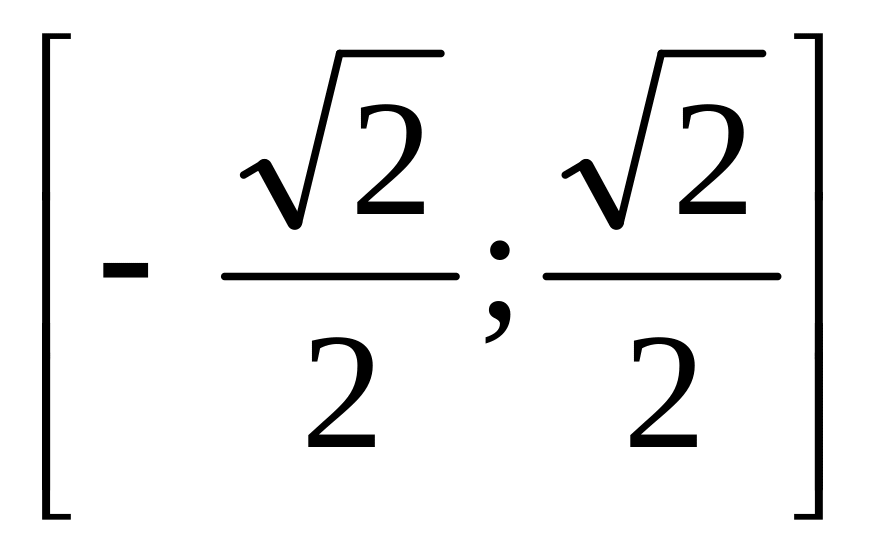 .
.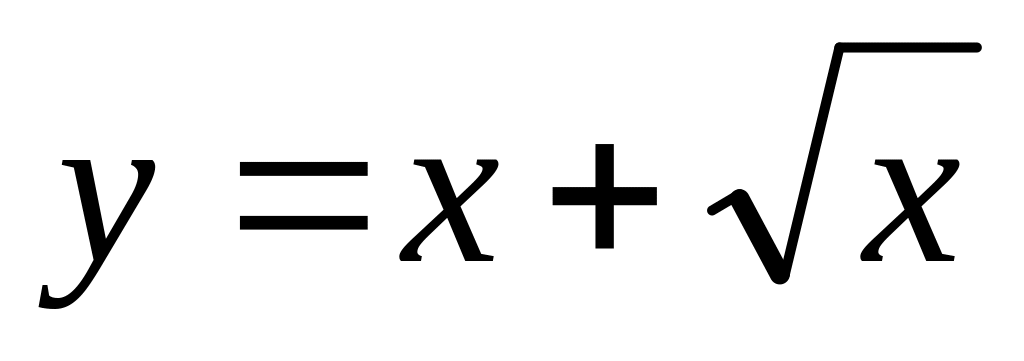 ,
.
,
.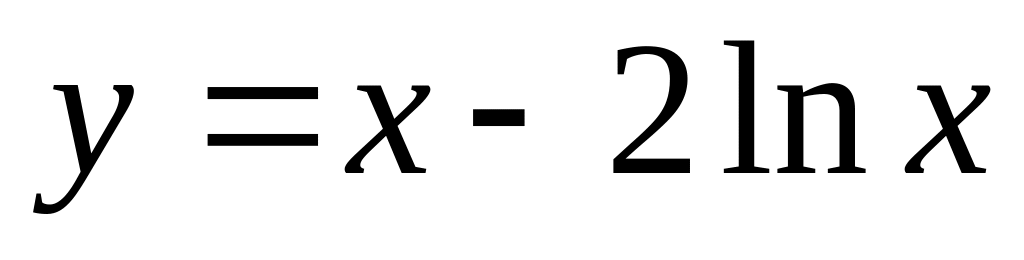 ,
,
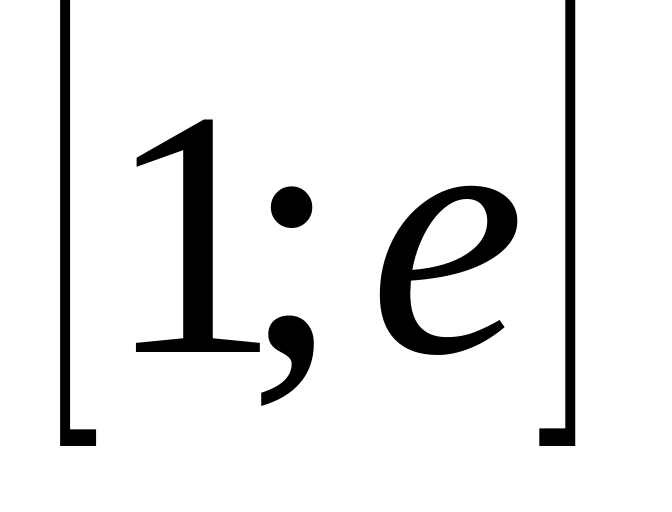 .
. ,
,
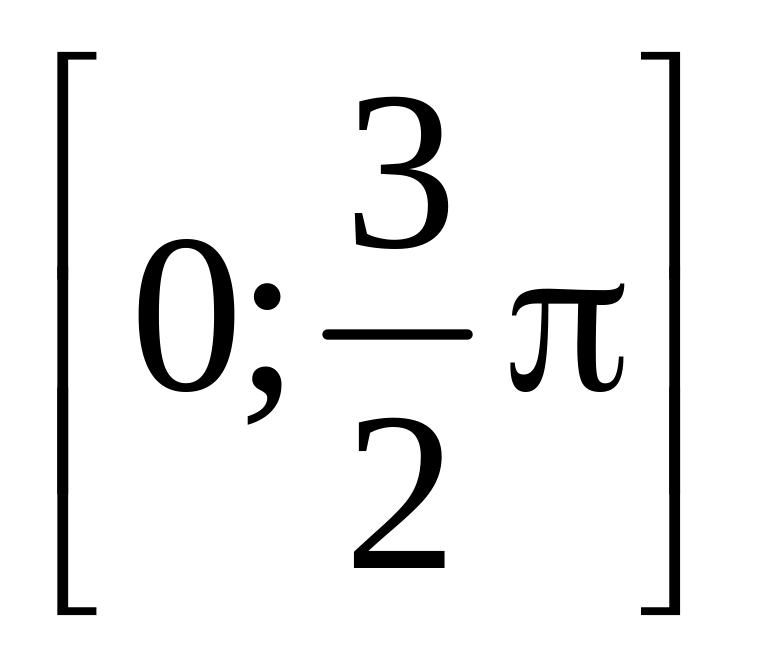 .
.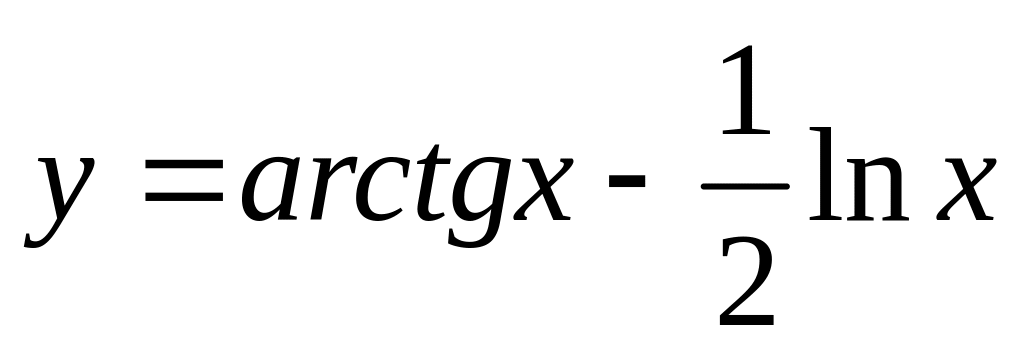 ,
,
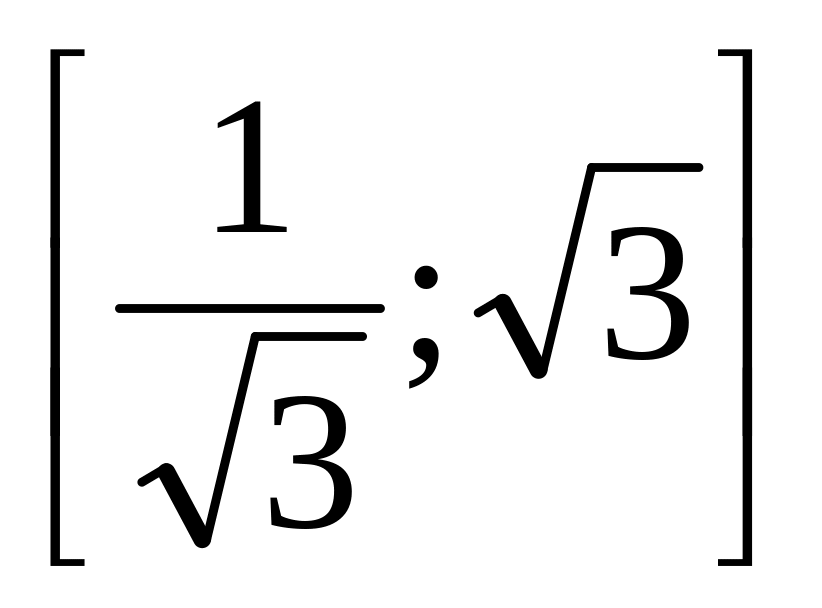 .
.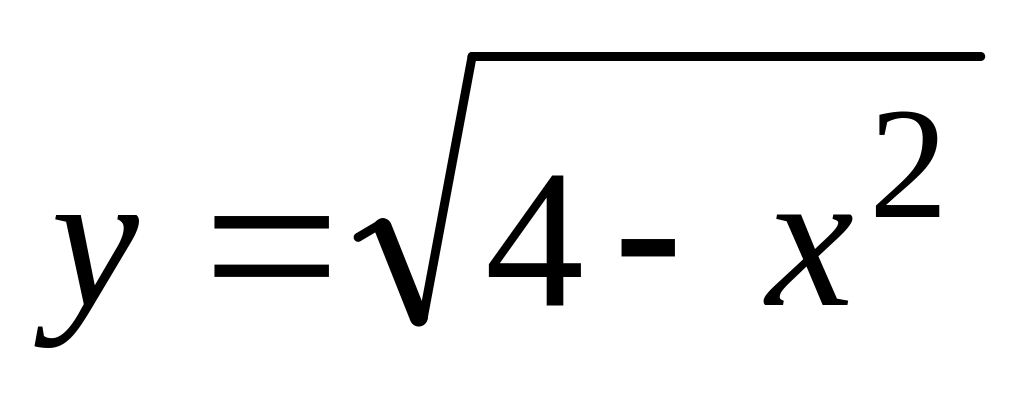 ,
.
,
. ,
,
 .
.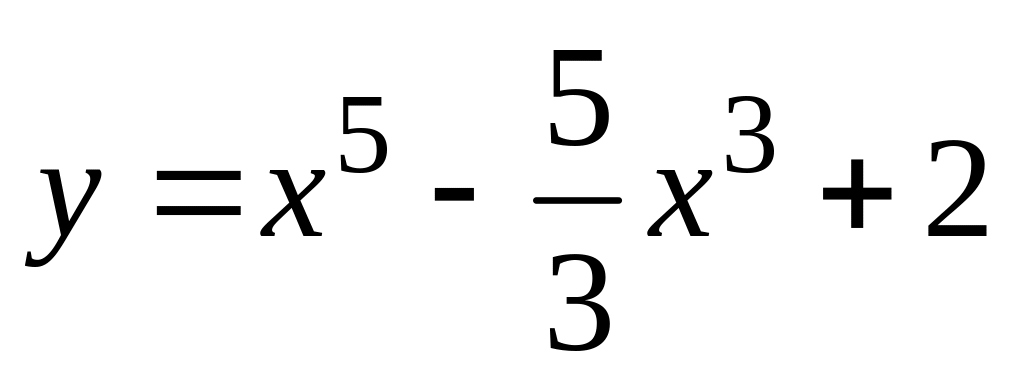 ,
,
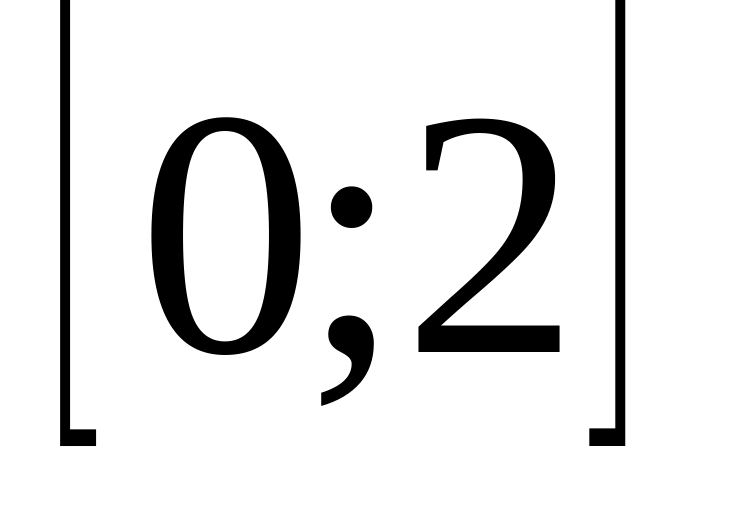 .
. ,
,
 .
.,
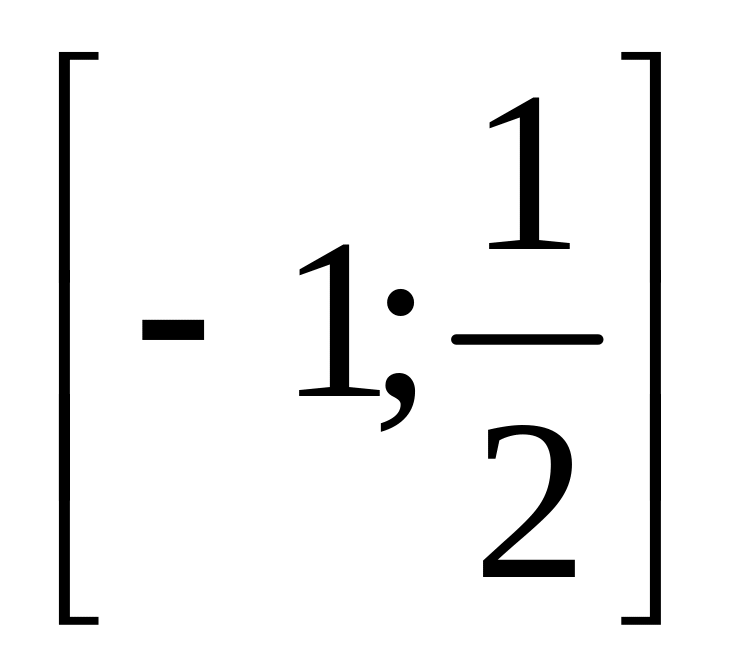 .
. ,
,
 .
. ,
.
,
.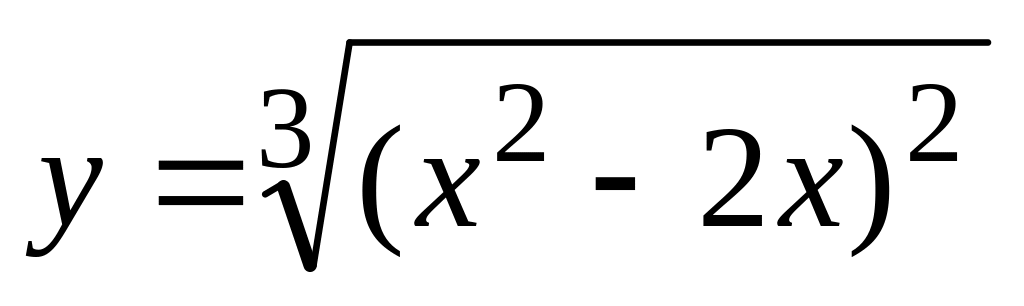 ,
.
,
.,
 .
.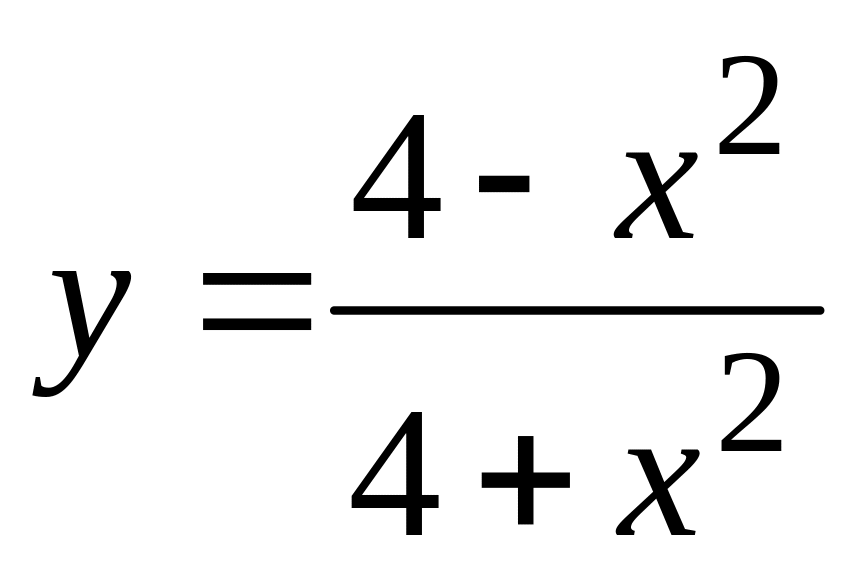 ,
,
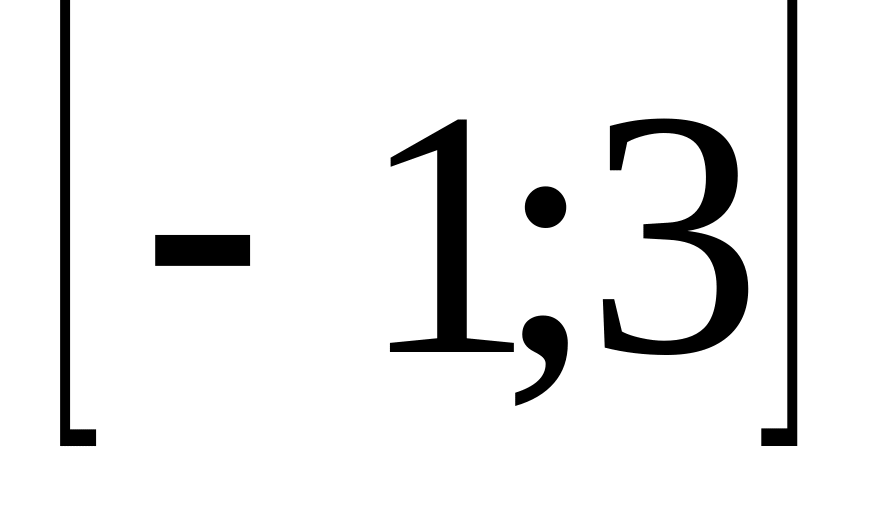 .
.
