Метод вариации произвольных постоянных

Пусть известно общее решение соответствующего однородного уравнения (13.14)

у₀=С₁у₁(х)+С₂у₂(х).

Найдем частное решение уравнения (13.13) данным методом. Будем искать частное решение неоднородного уравнения (13.13) в виде

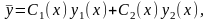(13.15)

рассматривая С₁ и С₂ как некоторые искомые функции от х.

Продифференцируем последнее равенство:

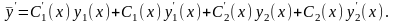
Для простоты подберем функции С₁ и С₂ так, чтобы выполнялось равенство

С¢₁(х)у₁(х)+С¢₂(х)у₂(х)=0.

Тогда предыдущее равенство примет вид

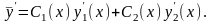
Дифференцируя это равенство найдем у¢¢

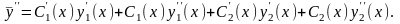
Подставляя выражения для у, у¢ и у¢¢ в уравнение (13.13) и группируя слагаемые, получим

Таким образом функция (13.15) является решением уравнения (13.13), если С₁(х) и С₂(х) удовлетворяют уравнениям системы

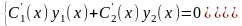(13.16)

в которой С¢₁(х) и С¢₂(х)-неизвестны, а у₁, у₂, у¢₁, у¢₂, f(x)-известны. Так как определителем этой системы является определитель Вронского

составленный из линейно независимых решений у₁(х) и у₂(х) однородного уравнения (13.14), то он не равен нулю, а значит система (13.16) имеет единственное решение относительно С¢₁(х) и С¢₂(х). Решая эту систему получим

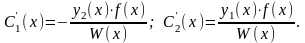
Интегрируя, найдем С₁(х) и С₂(х):

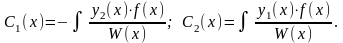
Подставляя их в (13.15) получим искомое частное решение уравнения (13.14).

13.7. Линейные однородные уравнения второго порядка с постоянными коэффициентами

Определение. Уравнение вида

у  + р у + q y = 0, (13.17)

где р, q  вещественные числа, называется линейным однородным уравнением второго порядка с постоянными коэффициентами.

Определение. Пусть дано линейное однородное уравнение второго порядка с постоянными коэффициентами (13.17).

Уравнение вида

k² + p k + q = 0 (13.18)

называется характеристическим уравнением уравнения (13.17).

Т е о р е м а 13.6. (о частных решениях уравнения (13.17)).

Если число k  действительный корень уравнения (13.18), то у = e^kx является частным решением уравнения (13.17).

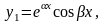
Если k_{1, 2} =  ±  i  комплексно сопряженные корни уравнения (13.16), то функции 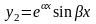являются частным решением уравнения (13.15).

Т е о р е м а 13.7. (об общем решении уравнения (13.17)).

Если корни характеристического уравнения (13.18) вещественные и различные (k₁  k₂), то общее решение уравнения (13.17) имеет вид

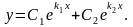
Если корни уравнения (13.18) вещественные и равные (k₁ = k₂), то общее решение уравнения (13.17) имеет вид

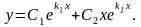
Если корни характеристического уравнения (13.18) комплексные 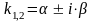, то общее решение (13.17) имеет вид

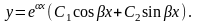
13.8. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами

Определение. Уравнение вида

у ¢¢ + р у ¢ + q y = f (x) (13.19)

где р, q – вещественные числа, называется линейным неоднородным уравнением второго порядка с постоянными коэффициентами.

Определение. Функцию f (x) будем считать специальной, если она представляет собой многочлен, или показательную функцию или тригонометрическую функцию sin bx или cos bx, или линейную комбинацию перечисленных функций.

Для уравнения (13.19) существует более простой метод нахождения частного решения , вид которого зависит от вида правой части f (x) этого уравнения.

Частное решение неоднородного уравнения может быть найдено по методу неопределенных коэффициентов:

1. по виду правой части уравнения (13.19) записывается форма частного решения с неопределенными коэффициентами;

2. затем таким образом сформированное частное решение подставляется в дифференциальное уравнение (13.19);

3. из полученного тождества определяются значения коэффициентов.

Запишем виды частных решений уравнения (13.19) для различных правых частей в виде таблицы.

Виды частных решений для различных правых частей линейных неоднородных дифференциальных уравнений

у  + р у  + q y = f (x)

Правая часть f (x)	Корни характеристического уравнения k2+ pk + q = 0	Вид частного решения
1. Рn(x)	k1, 2  0	Qn(x)
	k1 = 0, k2  0	xQn(x)
	k1, 2 = 0	x2Qn(x) Qn(x) – многочлен степени п с неопределенными коэффициентами.
2. аex	k1, 2  	Aex
	k1 = , k2  	Axex
	k1, 2 = 	Ax2ex
3. exPn(x)	k1, 2  	exQn(x)
	k1 = , k2  	xexQn(x)
	k1, 2 = 	x2exQn(x) Qn(x) – многочлен степени п с неопределенными коэффициентами.
4. а∙cos x а∙sin x а∙cos x + b sin x	k1, 2  ± i∙	А cos x + В sin x
	k1, 2 = ± i∙	(А cos x + В sin x)∙ х, А, В – неопределенные коэффициенты.
5. Pn(x) cos x Pn(x) sin x Pn(x) (cos x + sin x)	k1, 2  ± i∙	Rn(x)cos x+Sn(x)sin x
	k1, 2 = ± i∙	x(Rn(x)cos x+Sn(x)sin x) Qn(x) – многочлен степени п с неопределенными коэффициентами.
6. ex cos x ex sin x ex (a cos x + b sin x)	k1, 2   ± i∙	ex(А cos x + В sin x)
	k1, 2 =  ± i∙	ex х (А cos x + В sin x) А, В – неопределенные коэффициенты.
7. ex Pn(x) cos x ex Pn(x) sin x ex Pn(x) (cos x + sin x)	k1, 2   ± i∙	ex(Rn(x)cos x+Sn(x)sin x)
	k1, 2 =  ± i∙	xex(Rn(x)cos x+Sn(x)sin x) Qn(x) – многочлен степени п с неопределенными коэффициентами.
8. ex(Pn(x)∙cos x + + Qm(x)∙sin x)	k1, 2   ± i∙	ex(Rd(x)∙cos x + Sd(x)∙sin x)
	k1, 2 =  ± i∙	xex(Rd(x)cos x+Sd(x)sin x) Rd(x), Sd(x) – многочлены степени d = max (n, m) с неопределенными коэффициентами.