Лабораторная работа 6

Федеральное агенство по образованию РФ

СПбГЭТУ «ЛЭТИ»

Кафедра МО-ЭВМ

Факультет КТИ

ОТЧЕТ

по лабораторной работе № 6

Метод простых итераций.

Дисциплина: вычислительная мпатематика

Студент группы 4351

Кузьменко А.

Преподаватель:

Щеголева Н.Л.

Санкт-Петербург

2006

Лабораторная работа № 6

Метод простых итераций.

1. Постановка задачи.

Найти корень уравнения для функции с заданной точностью Eps методом простых итераций, исследовать скорость сходимости и обусловленность метода.

2. Теоретические сведения.

Метод простых итераций решения уравнения состоит в замене исходного уравнения эквивалентным ему уравнением и построении последовательности , сходящейся при n   к точному решению.

Если функция определена и дифференцируема на отрезке [a, b] и все ее значения то, если существует q, такое, что , то процесс итерации сходится при , и предельное значение – единственный корень уравнения на отрезке [a, b]

Рассмотрим один шаг итерационного процесса. Исходя из найденного на предыдущем шаге значения , вычисляется . Если , то принимается x_n = y и выполняется очередная итерация. Если же , то вычисления заканчиваются, и за приближенное значение корня принимается величина x_n = y. Погрешность результата вычислений зависит от знака производной при погрешность определения корня составляет , а при погрешность не превышает .

Для применения метода простых итераций определяющее значение имеет выбор функции в уравнении , эквивалентном исходному. Функцию необходимо подбирать так, чтобы . Это обусловливается тем, что если на отрезке (a, b), то последовательные приближения будут колебаться около корня c, если же , то последовательные приближения будут сходиться к корню c монотонно. Следует также помнить, что скорость сходимости последовательности {x_n} к корню c функции тем выше, чем меньше число q.

3. Анализ задачи.

Составим уравнение эквивалентное исходному . Исходное уравнение имеет 5 корней:

Составить функцию , удовлетворяющую условиям сходимости метода итераций для всех корней одновременно довольно проблематично.

Пусть. График функции выглядит следующим образом (также приведен график y=x):

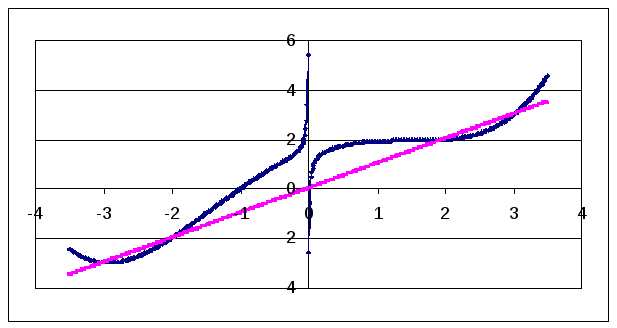
Условиям сходимости для корня x₁ удовлетворяет интервал [-3.22, -2.56], а для корня x₄ – интервал [0,34, 2.54], в окрестностях остальных корней .

Если , то график выглядит следующим образом:

И возможно найти корни x₂ и x₅ (интервалы сходимости соответственно – [-2.55, -0.15] и [2.55, 3.22] ).

Для того, чтобы найти корень x₃ построим функцию . Ее график имеет вид:

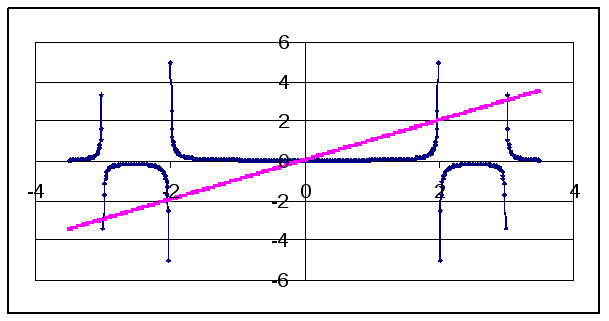
Интервал сходимости – [-1.34, 1.77].

Всем интервалам сходимости, приведенные выше, соответствует , для уменьшения q необходимо ограничивать интервалы.

4. Текст программ.

Приведен текст программы для

double ITER(double X0,double Eps,int &N)

{

if(Eps<=0.0){puts("Неверное задание точности\n");getch();exit (1);}

double X1=F(X0);

double X2=F(X1);

N = 2;

while( (X1 - X2)*(X1 - X2) > fabs((2*X1-X0-X2)*Eps) )

{

X0 = X1;

X1 = X2;

X2 = F(X1);

N++;

}

return(X2);

}

#include "methods.h"

double delta;

void main()

{

int k;

long int s;

float eps1,delta1,a1;

double eps,x0,x;

printf("введите delta:");

scanf("%f",&delta1);

delta = delta1;

printf("введите eps:");

scanf("%f",&eps1);

eps = eps1;

printf("введите x0:");

scanf("%f",&a1);

x0 = a1;

x = ITER (x0,eps,k);

printf("x=%f k=%d\n",x,k);

getch();

}

double F(double x)

{

extern double delta;

double s;

if (x==0) {printf ("деление на  0!"); getch(); exit(1);}

{ s = x + 0.04*( (pow(x,4))-(13*(x*x))+36-(1/x) );

s = Round( s,delta );

return(s);

}

}

double F1(double x)

{

extern double delta;

double s;

if (x==0) {printf ("деление на  0!"); getch(); exit(1);}

{ s = 1 + 0.04*( 4*pow(x,3)-26*x+1/(x*x) );

s = Round (s,delta);

return(s);

}

}

5. Вычислительный эксперимент.

С помощью описанных ранее функций φ(x) и составленных на их основе программ, найдем значения корней исходного уравнения (с разной точностью).

Исходные данные: x01=-2.6, x02=-2.5, x03=1.7, x04=0.4, x05=3.2, delta=0.000001.

eps	x1	k1	x4	k4	x2	k2	x5	k5	x3	k3
0,1	-2,990491	3	1,946682	2	-2,04655	3	3,018182	2	0,027997	2
0,01	-2,990491	3	1,969991	3	-2,029841	4	3,009072	3	0,027997	2
0,001	-2,988378	4	1,974081	4	-2,025262	6	3,009072	3	0,027786	3
0,0001	-2,988718	5	1,974987	6	-2,025089	7	3,010933	6	0,027786	3
0,00001	-2,988665	6	1,975014	7	-2,025044	9	3,010902	7	0,027786	3
0,000001	-2,988672	8	1,97502	9	-2,025042	10	3,010907	9	0,027786	3

Для исследования сходимости метода рассмотрим процесс нахождения корня x₄ . Возьмем различные интервалы сходимости, так, чтобы проследить зависимость скорости сходимости от числа q=max |φ(x)|.

[a,b]	q	[a,b]	q	[a,b]	q
[0.34, 2.54]	1	[0.48, 2.38]	0.7	[0.71, 2.18]	0.4
	0.9	[0.55, 2.32]	0.6	[0.82, 2.09]	0.3
[0.43, 2.44]	0.8	[0.62, 2.25]	0.5	[0.95, 1.98]	0.2

Тогда, при выборе x0 из указанных интервалов, получим различное количество итераций (delta=eps=0.000001):

0,34	9	2,54	10	Видно, что чем меньше число q, тем быстрее сходится итерационный процесс.
0,38	9	2,49	9
0,43	9	2,44	9
0,48	9	2,38	9
0,55	9	2,32	9
0,62	8	2,25	8
0,71	8	2,18	8
0,82	8	2,09	8
0,95	8	1,98	6

Исследуем скорость сходимости на примере интервала [0.82, 2.09], где q=0,3. Размер каждого следующего интервала между приближениями через предыдущий можно оценить по формуле: .

Пусть delta=eps=0.000001, x0=2.09, тогда:

n	xn	(xn - xn-1)теор	(xn - xn-1)практ	Видим, что оценка верна и (xn - xn-1)теор < (xn - xn-1)практ
0	2,09
1	2,002661	0,857142857	0,087339
2	1,980562	0,037431	0,022099
3	1,97608	0,009471	0,004482
4	1,975221	0,001920857	0,000859
5	1,975059	0,000368143	0,000162
6	1,975028	6,94286E-05	3,1E-05
7	1,975022	1,32857E-05	6E-06
8	1,975021	2,57143E-06	1E-06

Исследуем обусловленность метода простых итераций на примере этого же корня. Число обусловленности задачи _=1/|f (1,975021)| = 0,04931. Задана требуемая точность eps=0,0001 и при различной задаваемой точности вычисления функций задача имеет разную обусловленность.

В столбце “теоретически” вычисляется отношение eps/delta и выводится “да”, если _ меньше его (задача хорошо обусловлена) и “нет” в обратном случае. В столбце “практически” вычисляется разность найденного значения x и эталона (значения корня с наименьшей погрешностью) и выводится “да”, если это значения меньше заданной точности результата (eps). В результате получим:

x0	eps	delta	x	теоретически		практически
2	0,00000001	1E-08	2	eps/delta	обусл	погр y	соотв
0,5	0,0001	0,01	2	0,01	нет	0,00502	нет
1,5	0,0001	0,003333	2	0,03	нет	0,00033	нет
0,4	0,0001	0,002	2	0,05	да	0,00102	нет
2,1	0,0001	0,001429	2	0,07	да	0,00019	нет
0,4	0,00001	0,000125	2	0,08	да	2,1E-05	нет
1,4	0,00001	0,000111	2	0,09	да	0,0006	нет
1,9	0,00001	0,0001	2	0,1	да	2,1E-05	нет
0,6	0,00001	3,33E-05	2	0,3	да	1,8E-05	нет
1,5	0,0001	0,0002	2	0,5	да	2,1E-05	да
0,35	0,00001	0,00002	2	0,5	да	1E-06	да
2,53	0,00001	1,67E-05	2	0,6	да	5E-06	да
2,2	0,00001	1,43E-05	2	0,7	да	0	да
0,7	0,00001	1,25E-05	2	0,8	да	9E-06	да
1,6	0,000001	1,11E-06	2	0,9	да	0	да
0,9	0,000001	0,000001	2	1	да	1E-06	да

6. Выводы.

Метод простых итераций довольно прост с точки зрения вычислений и имеет достаточно быструю сходимость. Однако для его применения необходимо провести предварительный анализ задачи для нахождения функции φ(x). При этом, если функция имеет несколько корней, которые необходимо найти, то отыскание одной функции φ(x) проблематично.

Скорость сходимости метода зависит от функции φ(x). Также для успешного применения этого метода необходимо знать достаточно хорошее приближение корня, как и в методе Ньютона.

Поскольку очередной элемент итерационной последовательности вычисляется с точностью вычисления функции φ(x) (delta), то независимо от числа обусловленности конкретной задачи метод дает результат, соответствующий требуемой точности, только если она не превосходит delta.