Лекция 4. Методы многомерной оптимизации

4.1.Метод Нелдера-Мида

Симплекс-метод нахождения локального минимума функции от нескольких переменных изобретен Нелдером и Мидом. Данный метод считается самым эффективным из прямых методов поиска экстремума. В двухмерном пространстве симплекс – это треугольник заданный тремя точками (вершинами), в трехмерном пространстве симплекс формируют вершины тетраэдра. В n-мерном пространстве симплекс формируется вершинами из n+1 точек.

Для двух переменных симплексом является треугольник, и метод – это схема поиска, который сравнивает значения функции в трех вершинах треугольника. Наихудшая вершина, в которой функция f(x,y) принимает наибольшее значение, отбрасывается и заменяется новой вершиной. Формируется новый треугольник, и поиск продолжается. При этом строится последовательность треугольников (они могут иметь различную форму), значения функции, в вершинах которой становятся все меньше и меньше. Уменьшается размер треугольника, и координаты точки минимума найдены.

В формулировке алгоритма используется термин "симплекс" (обобщенный n-мерный треугольник). С его помощью находим минимум функции от n переменных. Он эффективен и компактен при вычислении.

Геометрическая интерпретация преобразований симплекса приведена для двумерного пространства. В симплексном методе применяются операции преобразования симплекса: отражение, растяжение, сжатие.

Исходный треугольник BGW

Предположим, что нужно минимизировать функцию . Для начала зададим три вершины треугольника. Вычислим значения функции в каждой вершине. Введем обозначения: В – наилучшая вершина (где значение ЦФ наименьшее), G – хорошая (следует за наилучшей) и W – наихудшая вершина (значение ЦФ наибольшее). Упорядочим значения функции таким образом, чтобы .

Средняя точка хорошей стороны

При построении используется средняя точка отрезка, соединяющего лучшие вершины В и G. Находим ее посредством усреднения координат:

Отражение, использующее точку R

Функция убывает при движении вдоль стороны треугольника от вершины W к вершине В так же, как при движении вдоль стороны от вершины W к G. Следовательно, существует возможность, что функция принимает наименьшие значения в точках, которые лежат вдали от вершины W на противоположной стороне между вершинами В и G. Выберем для проверки точку R, т. е. точку, полученную путем "отражения" треугольника относительно стороны BG. Чтобы найти R, сначала определяем среднюю точку М стороны BG. Затем проводим линию от вершины W к М и обозначаем длину полученного отрезка через d. Этот отрезок продолжается через точку М на длину d до точки R (рис. 4.1).

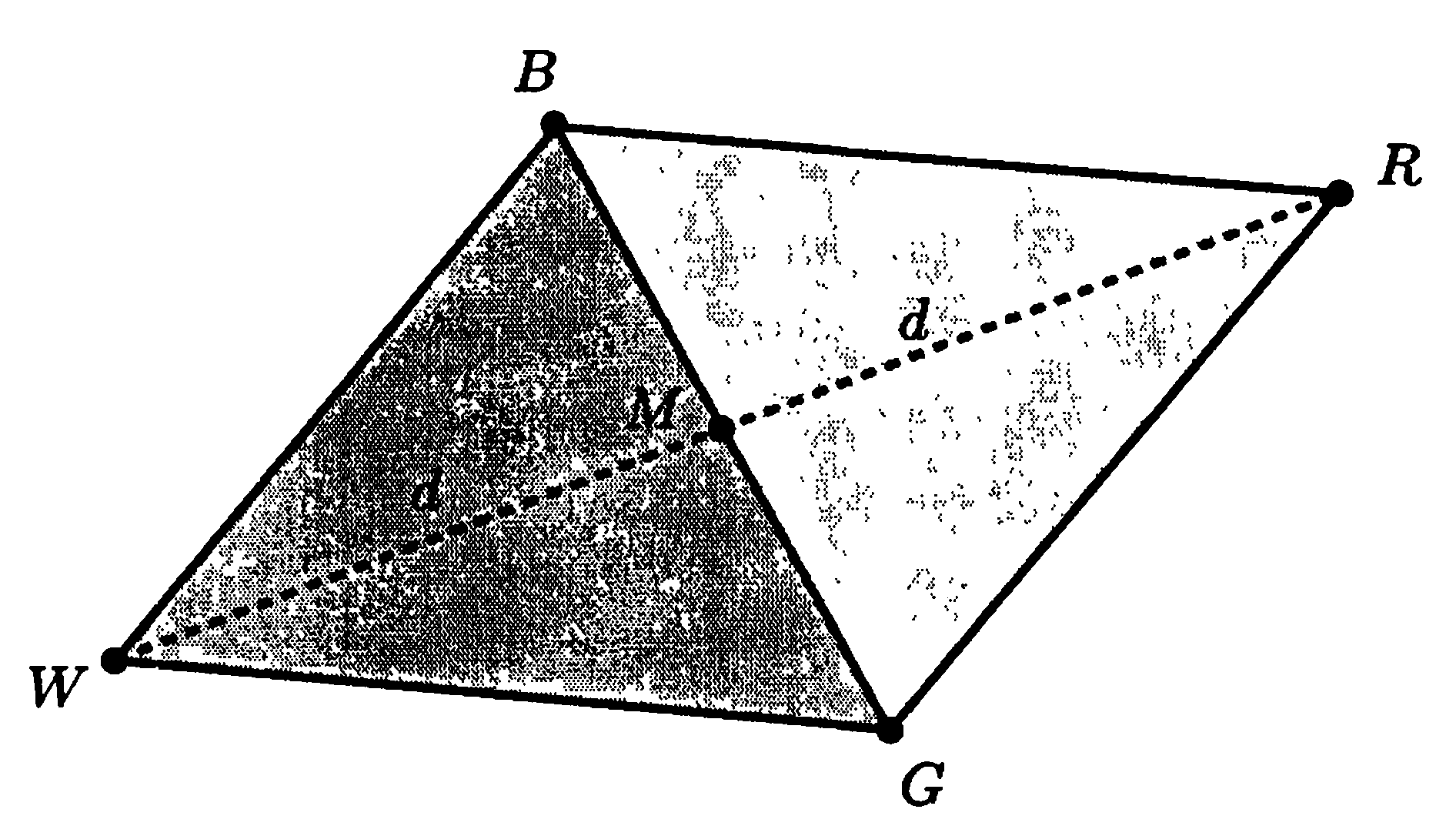
Рис. 4.1. Треугольник BGW, средняя точка М и отраженная точка R для метода Нелдера-Мида

Формула для вектора R имеет вид

R = М + (М – W) = 2М – W.

Расширение, использующее точку Е

Если значение функции в вершине R меньше значения функции в вершине W, то выбрано правильное направление в сторону минимума. Возможно, минимум находится несколько дальше, чем точка R. Поэтому продлим отрезок через вершины М и R к точке Е. Получится вытянутый треугольник BGE. Точку Е находим, двигаясь на расстояние d вдоль линии, соединяющей вершины М и R (рис. 4.2).

Рис. 4.2. Треугольник ABGW, точка R и продолженная точка Е

Если значение функции в вершине Е меньше значения функции в вершине R, значит, найдена лучшая вершина, чем R. Формула для вектора Е имеет вид

Е = R + (R - М) = 2R - М.

Сжатие, использующее точку С

Если значения функции в точках R и W одинаковы, следует проверить другую точку. Возможно, значение функции меньше в точке М, но нельзя заменять вершину W точкой М, так как три точки должны составлять треугольник. Рассмотрим две средние точки С₁ и С₂, которые лежат на отрезках WM и MR соответственно (рис. 4.3).

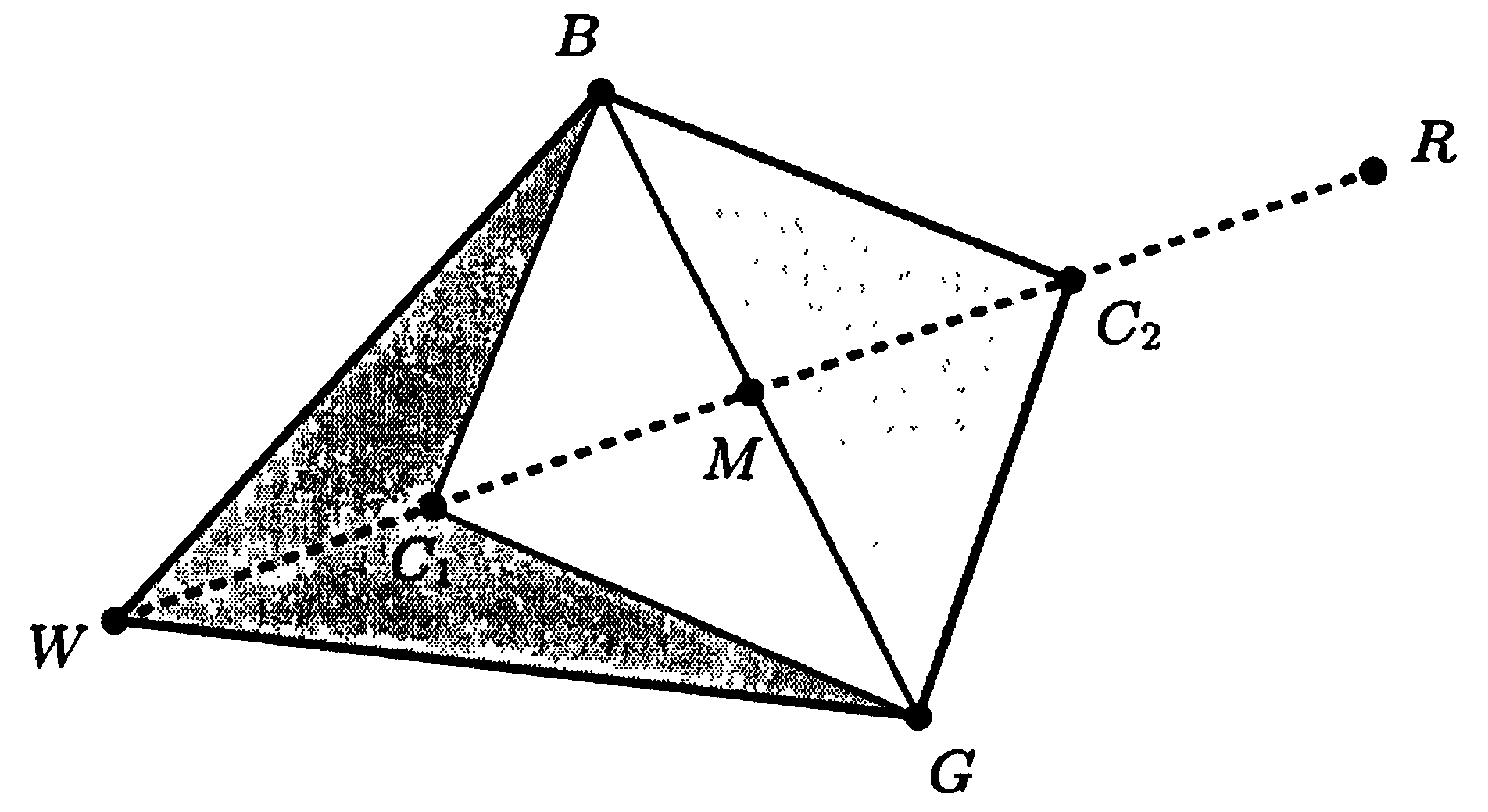
Рис. 4.3. Сжатие точки С₁ или С₂ для метода Нелдера-Мида

Точку, в которой функция принимает наименьшее значение, обозначаем через С и получаем новый треугольник BGC.

Сокращение по направлению к В

Если значение функции в точке С не меньше, чем значение в W, точки G и W следует "стянуть" к точке В (рис. 4.4).

Рис. 4.4. Сокращение треугольника к точке В

Точку G заменяем точкой M, a W – точкой S, которая является средней точкой на отрезке, соединяющем точки В и W.

Численно эффективный алгоритм будет вычислять функцию только при необходимости. На каждом шаге находим новую вершину, которой заменяем вершину W. После ее нахождения в дальнейшем исследовании не будет необходимости и шаг итерации будет завершен.

Алгоритм Нелдера-Мида

1. Задать начальный симплекс, вычислить значения ЦФ в вершинах симплекса, выбрать вершины B, W, G.

2. Если выполнены условия окончания поиска, то объявить точку B минимумом и перейти на 500

3. Выполнить операцию отражения для получения вершины R.

4. Если f(R) < f(G), то перейти на 5 (отражение, либо растяжение)

Иначе перейти на 6 (сжатие либо растягивание)

5. Если f(B) < f(R) то заменить W на R,

иначе вычислить Е и f(E),

Если f(E) < f(B) то замена W на Е

иначе замена W на R.

Перейти на 2

6. Если f(R) < f(W) то

замена W на R

Вычислить С = (М+ R)/2 или С = (М+ R)/2 и f(С)

Если f(С) < f(W) то замена W на С

иначе вычислить S и f(S)

замена W на S, замена G на M

Перейти на 2.

7. Конец алгоритма

Поиск минимума ЦФ завершается, когда размеры симплекса или разность между значениями в вершинах симплекса становятся достаточно малыми. Часто используют дисперсия

где – значения ЦФ в вершинах симплекса, – среднее значение ЦФ в вершинах симплекса

.

Выполнение условий окончания поиска соответствует либо малому ребру симплекса, либо попаданию стационарной точки внутрь симплекса, либо одновременному выполнению обоих условий.

Основным преимуществом симплексного метода является воз­можность работы с большим симплексом, т. е. сильно разнесенными точками. Это помогает избежать сжатия симплекса в точке локального минимума. Симплексный метод предпочтителен при выявлении области минимума функции ошибок, т. е. начального приближения к точке минимума при переходе к другим методам оптимизации.