
1.2 Поперечно-электрические поля
Чтобы определить типы электромагнитных волн в прямоугольном волноводе и проанализировать структуру электромагнитных полей, необходимо решить уравнение (15) при общих граничных условиях (3). Применительно к поперечно-электрическому полю ( или ) граничные условия имеют вид
![]() при
при ![]() ;
; ![]() ;
;
![]() при
при ![]() ;
; ![]() . (21)
. (21)
Используя выражения (17), при условии (21) получаем
![]() при
;
;
при
;
;
![]() при
;
. (22)
при
;
. (22)
Напомним, что для (или ) поля .
Решение волнового уравнения (15) осуществляется методом разделения переменных. Будем искать решение в виде
![]() , (23)
, (23)
где
![]() и
и
![]() -
функции, зависящие только от
-
функции, зависящие только от
![]() и
и
![]() соответственно.
Подставляя последние выражения в
уравнение (15), получим,
соответственно.
Подставляя последние выражения в
уравнение (15), получим,
![]() ,
,
откуда следует, что
![]() и
и ![]() ; (24)
; (24)
![]() ,
,
где
![]() и
и
![]() - произвольные постоянные разделения.
- произвольные постоянные разделения.
Как известно, общее решение уравнений (24), можно представить следующим образом:
![]() ,
,
![]() .
.
Следовательно,
в соответствии с (23) проекция
![]() будет равна
будет равна
![]() , (25)
, (25)
причем постоянная распространения в соответствии с (12) и (24) определяется как
![]() .
.
Чтобы найти входящие
в выражение для
![]() неизвестные величины, воспользуемся
граничными условиями (22). Из первого
условия вытекает, что
неизвестные величины, воспользуемся
граничными условиями (22). Из первого
условия вытекает, что
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Из второго условия получается:
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Таким образом,
![]() , (26)
, (26)
![]() , (27)
, (27)
![]() . (28)
. (28)
Здесь введено
обозначение
![]() .
.
Подставив значение
![]() в равенства (17) и (18), получим выражения
для комплексных амплитуд остальных
составляющих векторов электромагнитного
поля в прямоугольном волноводе для
поперечно-электрических волн
в равенства (17) и (18), получим выражения
для комплексных амплитуд остальных
составляющих векторов электромагнитного
поля в прямоугольном волноводе для
поперечно-электрических волн
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
Отметим, что при
![]() волны в волноводе существовать не могут,
так как в этом случае все компоненты
поля, за исключением
,
обращаются в нуль. Из этого следует, что
числа
и
волны в волноводе существовать не могут,
так как в этом случае все компоненты
поля, за исключением
,
обращаются в нуль. Из этого следует, что
числа
и
![]() могут принимать любые значения, равные
0,1,2,3,..., но не могут быть одновременно
равными нулю.
могут принимать любые значения, равные
0,1,2,3,..., но не могут быть одновременно
равными нулю.
Следовательно, в
прямоугольном волноводе могут существовать
бесчисленное множество типов
поперечно-электрических волн, определяемых
значениями чисел
и
.
Эти волны обозначаются символами
![]() (или
(или
![]() ).
В общем случае компоненты поля записываются
в виде суммы различных типов волн по
индексам
и
.
).
В общем случае компоненты поля записываются
в виде суммы различных типов волн по
индексам
и
.
Вдоль сторон
![]() и
и
![]() поперечного сечения волновода
распределение поля имеет характер
стоячей волны, причем величина
определяет число полуволн стоячей
волны, укладывающихся вдоль оси
на интервале
,
а
-
число
полуволн стоячей волны вдоль оси
на интервале
поперечного сечения волновода
распределение поля имеет характер
стоячей волны, причем величина
определяет число полуволн стоячей
волны, укладывающихся вдоль оси
на интервале
,
а
-
число
полуволн стоячей волны вдоль оси
на интервале
![]() .
.
Поле будет распространяться вдоль оси в виде бегущей волны, если постоянная распространения равна чисто мнимой величине
![]() , (29)
, (29)
где
![]() - фазовая
постоянная (продольное волновое число
волновода).
- фазовая
постоянная (продольное волновое число
волновода).
В противном случае поле в волноводе быстро уменьшается с расстоянием вследствие экспоненциального множителя .
Из выражений (27) и (29) следует, что
![]() . (30)
. (30)
С учетом сказанного продольная составляющая магнитного поля (28) примет вид
![]() . (31)
. (31)
Из равенства (30) следует, что в прямоугольном волноводе поперечно-электрическая волна ( ) при данных размерах и будет незатухающей, если
![]() .
.
Отсюда следует неравенство
![]() ,
,
или
![]() .
.
Величина
![]() (32)
(32)
имеет размерность
![]() и носит название критической частоты
волновода.
и носит название критической частоты
волновода.
Критической частоте соответствует критическая длина волны, которая определяется формулой
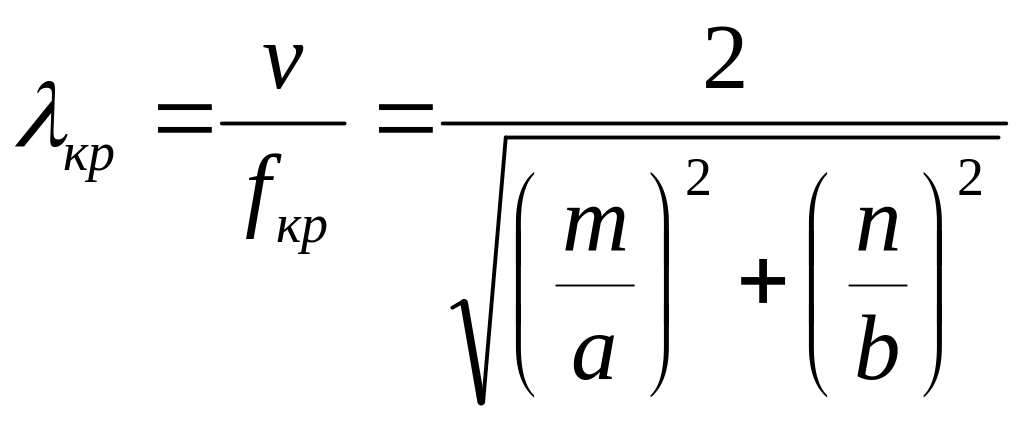 , (33)
, (33)
Таким образом, условие распространения волны по волноводу имеет вид
![]() или
или ![]() . (34)
. (34)
Фазовая скорость волны определяется по формуле
 , (35)
, (35)
а скорость переноса энергии равна
![]() . (36)
. (36)
Длина волны в волноводе определяется выражением
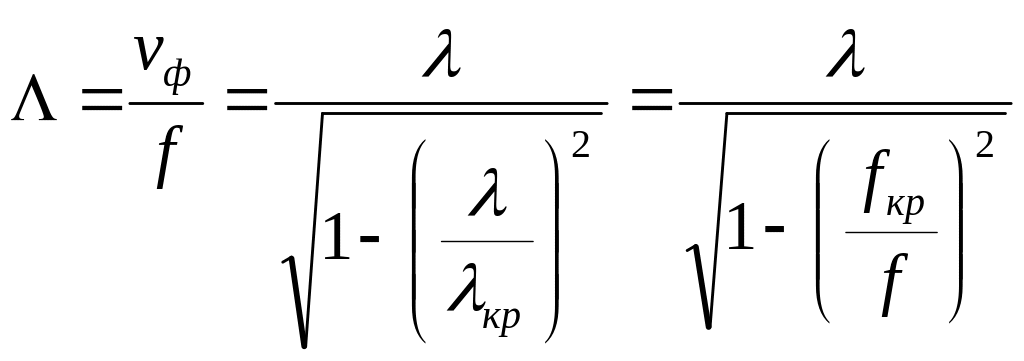 . (37)
. (37)
Из выражения (37) для длины волны в волноводе следует, что она отличается от длины волны в свободном пространстве и от длины волны в среде, заполняющей волновод.
Из выражения для фазовой скорости (35) видно, что волновод является дисперсной средой, так как фазовая скорость, а, следовательно, и скорость переноса энергии, зависит от частоты колебаний источника радиоволн.
При решении задач
теории волноводов, кроме понятия
волнового сопротивления среды
![]() ,
заполняющей волновод, пользуются
понятием характеристического сопротивления
волновода
,
заполняющей волновод, пользуются
понятием характеристического сопротивления
волновода
![]() .
Характеристическое сопротивление в
случае
.
Характеристическое сопротивление в
случае
![]() волн определяется в виде
волн определяется в виде
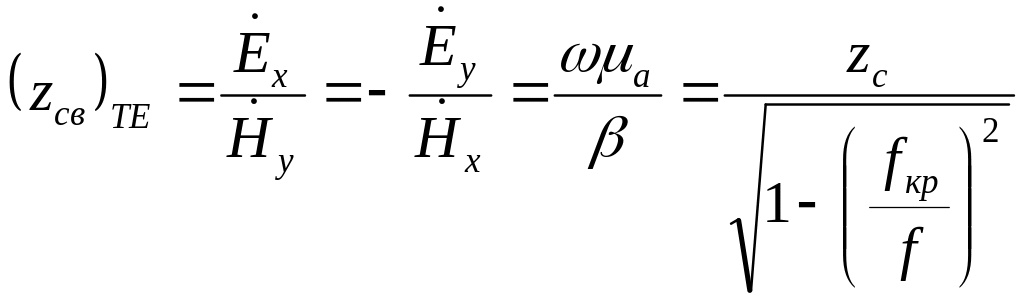 . (38)
. (38)
Из выражения (32)
следует, что при одинаковых размерах
поперечного сечения волновода критическая
частота растет с увеличением
и
,
т.е. высшие типы поперечно-электрических
волк (с большими значениями
и
)
имеют более высокие критические частоты
по сравнению с низшими типами.
Следовательно, для передачи электромагнитной
энергии при заданной частоте источника
колебаний по волноводу с наименьшими
поперечными размерами необходимо
возбуждать в нем волну с наименьшими
значениями
и
.
При размере
большем
это будет
волна
![]() (или
(или
![]() ).
Этот тип волны, называемый основным
типом волны в прямоугольном волноводе,
находит наибольшее применение на
практике.
).
Этот тип волны, называемый основным
типом волны в прямоугольном волноводе,
находит наибольшее применение на
практике.
Мощность, передаваемая
через поперечное сечение волновода
волной
![]() по определению равна
по определению равна
![]() , (39)
, (39)
где ![]() - поперечное сечение волновода;
- поперечное сечение волновода;
![]() -
продольная составляющая вектора
Пойнтинга [1,2].
-
продольная составляющая вектора
Пойнтинга [1,2].
Для прямоугольного
волновода эта величина равна
![]() ,
следовательно (приложение А)
,
следовательно (приложение А)
![]() , (40)
, (40)
где ![]() и
и
![]() - величины, комплексно-сопряженные
составляющим
- величины, комплексно-сопряженные
составляющим
![]() и
и
![]() соответственно.
соответственно.
Следует отметить, что правая часть выражения (39) справедлива лишь для волновода прямоугольного сечения.
