4 Тема 4. Определение стоимости денег во времени и ее использование в финансовых расчетах

Перед финансовым менеджером всегда стоит проблема: либо инвестировать средства в мероприятия с большей степенью прибыльности, но с большим риском и большим по продолжительности временем получения прибыли, либо выбрать вариант вложения с меньшей прибылью, но с большей гарантией возврата денежных средств в более короткие сроки. В этом случае прибыль можно получать регулярно и через непродолжительные сроки, что особенно важно в условиях инфляции.

С течением времени ценность денег изменяется, и «сегодняшние деньги» с точки зрения их покупательной способности имеют большее значение, чем «завтрашние». В результате сравнения различных вариантов прибыльности денежных вложений ключевое положение занимает ставка процента. В финансовом анализе она рассматривается не как категория денежного рынка, а как прикладной элемент всех денежных расчетов.

Процент – это доход от предоставления капитала в долг в различных формах, либо от инвестиций производственного или финансового характера, т.е. денежная его форма, величина в абсолютном выражении.

Процентная ставка – отношение процента к предоставляемому в долг капиталу, величина, характеризующая интенсивность начисления процентов. В финансовых расчетах используются две формы выражения процентной ставки. Величина получаемого дохода определяется, исходя из:

• величины вкладываемого капитала;

• срока, на который он инвестируется (предоставляется в долг);

• размера и вида процентной ставки.

Ставка процента показывает, в какой пропорции соотносится ценность сегодняшних и будущих денежных величин.

Ставка процента связана сформированием фондов потребления и накопления собственных средств.

Наращение (рост) первоначальной суммы долга – это увеличение суммы долга за счет присоединения начисленных процентов, дохода.

Множитель (коэффициент) наращения – величина, показывающая, во сколько раз возрос первоначальный капитал (отношение наращенной суммы к первоначальному капиталу).

Следует различать понятия периода и интервала начисления.

Период начисления – промежуток времени, за который начисляется процент. Как правило, период начисления совпадает со сроком, на который предоставляются деньги. Период начисления может разбиваться на интервалы начисления.

Интервал начисления – минимальный период, по прошествии которого происходит начисление процента.

При росте процентных платежей используются понятия первоначальной (теперешней) суммы долга и будущей (наращенной) стоимости вклада, т.е. стоимости вклада (кредита) с учетом прибавления к ней процентных платежей.

Содержание расчетов для наиболее прибыльного варианта денежных вкладов состоит в том, чтобы по известной теперешней стоимости капитала (настоящей, сегодняшней) определить будущие объемы выплат и наоборот исходя из будущей стоимости рассчитать теперешнюю.

В первом случае к теперешней стоимости прибавляется процент, а во втором – из будущей стоимости отнимается учетный (дисконтный) процент.

При вычислении будущей стоимости процент подлежит оплате в конце срока кредитования, при вычислении теперешней стоимости – выплачивается перед установленным сроком.

Существуют два способа определения и начисления процентов.

Декурсивный способ – проценты начисляются в конце каждого интервала начисления. Их величина определяется исходя из величины предоставленного капитала.

Декурсивная процентная ставка (ссудный %) – это выраженное в процентах (долях единиц) отношение суммы начисленного за определенный интервал дохода к сумме, имеющейся на начало данного периода.

Антисипативный способ (предварительный) – проценты начисляются в начале каждого интервала начисления, сумма процентных денег определяется из наращенной суммы.

Антисипативная процентная ставка (учетная ставка) – это выраженное в процентах (долях единиц) отношение суммы дохода, выплачиваемого за определенный интервал, к величине наращенной суммы, полученной по прошествии этого интервала.

В странах с развитой рыночной экономикой антисипативный способ применяется в период высокой инфляции. В мировой практике наибольшее распространение нашел декурсивный способ начисления и определения процентов. В украинской практике понятие ссудного процента и учетной ставки обычно не различается и обозначается собирательным термином «процентная ставка».

Простые и сложные ставки ссудного процента

Простые ставки ссудных процентов (декурсивных процентов) применяются обычно в краткосрочных финансовых операциях, когда интервал начисления совпадает с периодом начисления (и составляет, как правило, срок менее 1 года), или после каждого интервала начисления, по которому выплачиваются проценты.

Таким образом, если процент начисляется на исходную сумму, то ставка процента называется простая.

Введем следующие обозначения:

i, i (%) – простая годовая ставка ссудного процента;

I – процент или общая сумма процентных денег за весь период начисления;

І_г – сумма процентных денег, выплачиваемых за год;

Р – величина первоначальной денежной суммы (теперешняя, настоящая, современная стоимость);

S – наращенная сумма (будущая стоимость денег);

К_н – коэффициент наращения;

n – продолжительность периода начисления в годах;

– продолжительность периода в днях;

К – продолжительность года в днях.

В зависимости от способа определения продуктивности финансовой операции различают точный и обыкновенный (коммерческий) процент. При этом возможны два варианта:

1. используется точное число дней ссуды, определяемое по специальной таблице, где показаны порядковые номера каждого дня года, и из номера, соответствующего дню окончания займа, вычитают номер первого дня;

2. берется приблизительное число дней ссуды, когда продолжительность полного месяца принимается равной 30 дням. Этот метод используется, когда не требуется большая точность расчетов, при частичном погашении кредита.

Таким образом, возможны три варианта расчета наращенной суммы:

1 Точный процент получается, когда за временную базу берут фактическое число дней в году (К = 365 или 366 дней) и точное число дней ссуды.

2 Обыкновенный процент с точным числом дней ссуды содержит расчет с использованием приближенного числа дней в году (К = 360) и точного числа дней ссуды.

3 Обыкновенный процент с приближенным числом дней ссуды рассчитывается с приближенным числом дней в году и приближенным числом дней ссуды.

На практике используются разные системы приближенных расчетов (таблица 4.1).

Таблица 4.1 – Системы приближенных расчетов

Система	Число дней в месяце		Число дней в году	День приема / выдачи вклада
	Неполный месяц	Полный месяц
А) Германия	Факт	30	360	-1
Б) Англия	Факт	Факт	Факт	-1
В) Франция	Факт	Факт	365	-1

Формулы для определения этих величин следующие:

1. i(%) = (I_г/P)100% (4.1)

2. i = I_г/P (4.2)

3. I = I_гn (4.3)

4. S = Р+I (4.4)

5. К_н = S/P (4.5)

6. n = (4.6)

Используя данные формулы, получаем основные формулы для определения наращенной суммы:

, (4.7)

. (4.8)

Определение величины наращенной суммы S (будущей стоимости денег по известной первоначальной сумме денег) называется компаундингом.

На практике часто возникает обратная задача: по известной величине наращенной суммы определить необходимую величину первоначальной суммы. Определение величины первоначальной денежной суммы Р по заданной величине наращенной суммы S называется дисконтированием. Формулу, которая отражает операцию дисконтирования, получаем из формулы (4.7):

. (4.9)

Преобразуя формулу (4.7), получаем еще несколько формул для определения неизвестных величин:

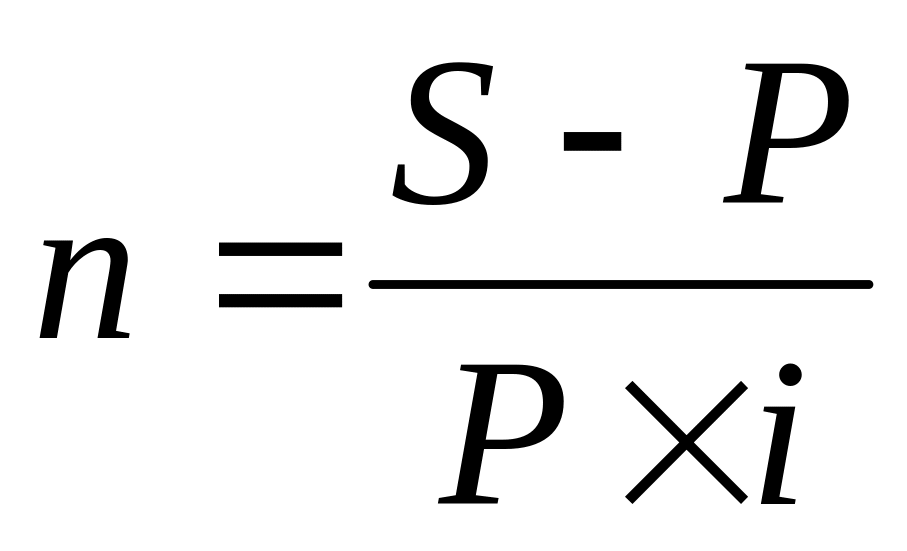1. (4.10)

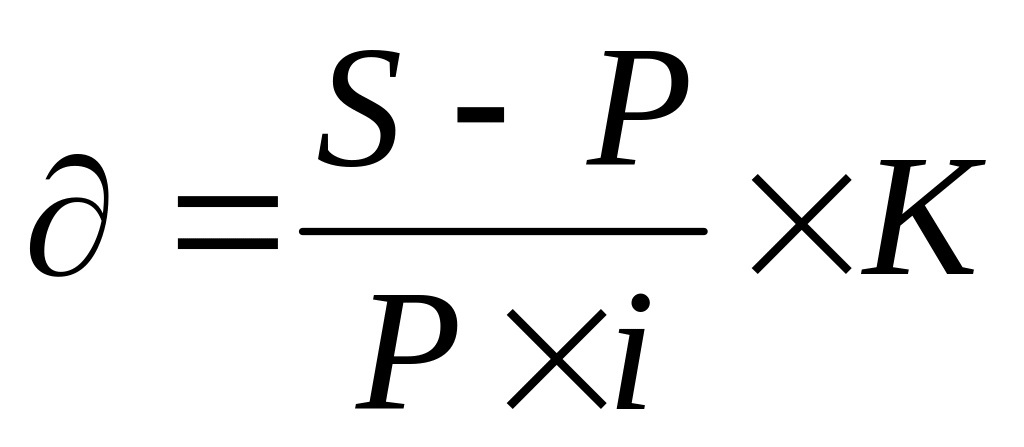2. (4.11)

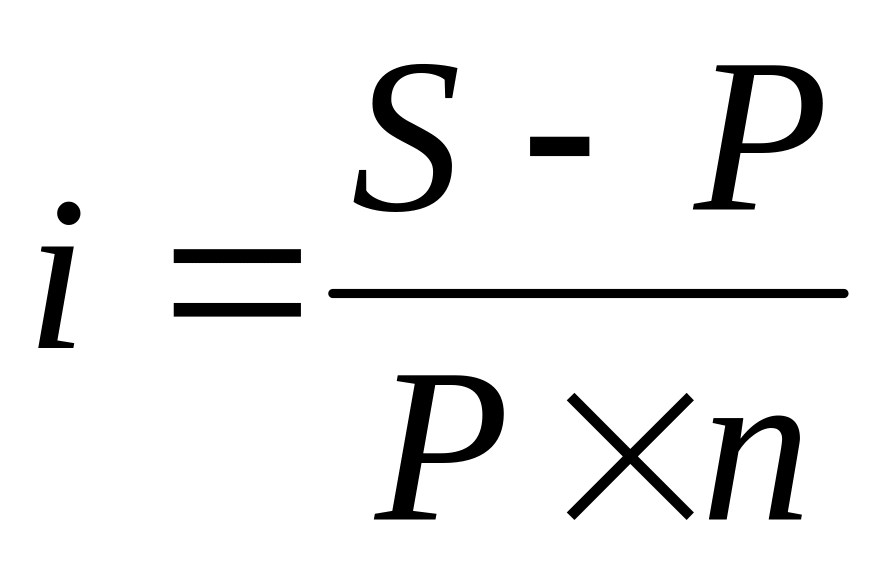3. (4.12)

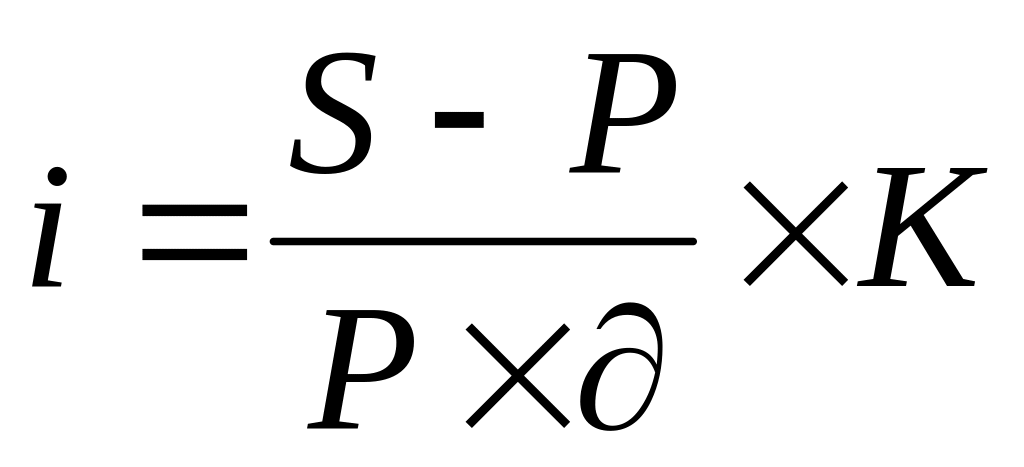4. (4.13)

Рассмотрим случай, когда на разных интервалах исчисления применяются разные процентные ставки. Если на последовательных интервалах начисления n₁, n₂, …, n_N используют ставки процента i₁, i₂, …, i_N, то сумма процентных денег в конце первого интервала начисления составит

.

В конце второго интервала начисления: и т.д….

При n интервалах начислений наращенная сумма составит

. (4.14)

Множитель начисления (коэффициент) будет равен

. (4.15)

Если после очередного интервала начисления доход, то есть начисленные за данный интервал проценты, не выплачиваются, а присоединяются к денежной сумме, имеющейся на начало этого интервала, то для определения наращенной суммы применяют формулу сложных процентов. Т.е. при реинвестировании дохода проценты начисляются на уже наращенную стоимость по сложной процентной ставке:

Введем обозначения:

i_c – годовая ставка сложного ссудного процента;

k_н.с – множитель (коэффициент) наращения в случае сложных процентов;

j – номинальная ставка сложных ссудных процентов.

Если за интервал начисления принимается год, то по прошествии первого года наращенная сумма в соответствии с формулой (4.7) составит

S₁= P(1+i_c)

Еще через год это выражение применяется уже к сумме S₁, то есть

S₂ = S₁(1+i_c) = P(1+i_c)² и т.д.

Очевидно, что по прошествии n лет, наращенная сумма составит:

S = P(1+i_c)ⁿ (4.16)

Множитель наращения будет равен

k_н.с = P(1+i_c)ⁿ (4.17)

Сравнивая данную формулу (4.17) с формулой коэффициента наращения для простых ставок ссудных процентов (4.5), можно отметить, что чем больше период начисления, тем больше разница в величине наращенной суммы при начислении простых и сложных процентов. Эту разницу можно наглядно представить с помощью графиков, изображенных на рисунке 4.1.

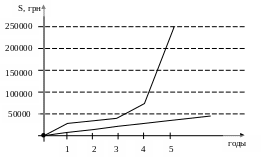
Рисунок 4.1 – Наращение вложенной суммы по простой и сложной

процентным ставкам (i = i_c = 200%)

Первоначальная сумма составляет 1000 грн. (на графике она сливается с нулевой точкой из-за значительности получаемых на следующих этапах сумм). Процентная ставка – 200% в год. Верхняя линия соответствует наращению денежной массы в случае применения сложной процентной ставки. Она представляет собой пример экспоненциального роста (чем больше n, тем круче кривая уходит вверх). Нижняя линия соответствует случаю простых процентов и является прямой с очень небольшим углом наклона.

Не всегда стоит отдавать предпочтение более высокой простой процентной ставке по сравнению с более низкой сложной суммой. Сумма, наращенная по сложной процентной ставке, уже через небольшое количество интервалов начисления может превысить сумму, наращенную по простой ставке (см. рис.4.1).

Если срок ссуды n (годы) не является целым числом, то коэффициент наращения рассчитывается по формуле

, (4.18)

где – целое число лет начисления;

– оставшаяся дробная часть года.

На практике предпочитают пользоваться формулой (4.17) с соответствующим нецелым показателем степени. Однако с точки зрения сущности начисления процента этот способ является приблизительным, и погрешность при вычислениях будет тем больше, чем больше значение входящих в формулу величин. Приблизительный метод дает меньший, чем в действительности, результат.

Рассмотрим случай, когда уровень ставки сложных процентов является разным на различных интервалах начисления.

Пусть n₁, n₂, …, n_N – продолжительность интервалов начисления в годах; i₁, i₂, …, i_N – годовые ставки процентов, соответствующие данным интервалам, тогда наращенная сумма в конце первого интервала начисления в соответствии с формулой (4.7) составит:

.

В конце второго интервала начисления составит

и т.д.

При N интервалах начисления наращенная сумма в течение всего периода начисления составит

. (4.19)

Если все интервалы начисления одинаковы (как это обычно бывает и на практике) и ставка сложного процента одинакова, то формула 4.19 принимает вид:

(4.20)

Начисление сложных процентов может осуществляться не один, а несколько раз в году. В этом случае оговаривается номинальная ставка процентов j – годовая ставка, исходя из которой определяется величина ставки процентов к применяемой на каждом интервале сумме начисления. При m равных интервалах начисления и номинальной процентной ставке j величина ставки процентов, применяемой на каждом интервале начисления, будет равна j/m.

Если срок ссуды составляет n лет, то аналогично формуле (4.17), получаем выражение для определения наращенной суммы

, (4.21)

где mn – общее число интервалов начисления за весь срок ссуды.

Если общее число интервалов начисления не является целым числом (произведение mn – целое число интервалов начисления, а – оставшаяся дробная часть интервала начисления), то выражение (4.21) принимает вид

. (4.22)

Т.е. для целого числа периодов начисления используется формула сложных процентов, а для оставшейся дробной части используется формула простых процентов (4.7).

В настоящее время наиболее распространенным является начисление процентов по полугодиям, поквартальное, ежемесячное, ежедневное. Такие проценты, начисляемые с определенной периодичностью, называются дискретными.

В мировой практике часто применяется также непрерывное начисление сложных процентов (т.е. продолжительность интервалов стремится к 0, а количество интервалов стремится к ). В этом случае для начисления наращенной суммы используются следующее выражение:

. (4.23)

Для практических результатов можно использовать известную в математике формулу

,

где – основание натурального логарифма.

Из этой формулы следует: .

Тогда для вычисления наращенной суммы получаем формулу

. (4.24)

Коэффициент наращения при непрерывном начислении сложных процентов дает максимальную величину наращенной суммы при прочих равных условиях, т.е. при одинаковых значениях n, j, P.

На рис. 4.2 показаны кривые роста первоначальной денежной суммы в 1000 грн.

При одинаковой номинальной процентной ставке 200% и различном количестве интервалов начисления в году m (1-я кривая – ежегодное начисление; 2-я – начисление по полугодиям; 3-я – поквартальное начисление; 4-я – ежемесячное; 5-я – непрерывное).

Чем короче интервал начисления, тем больше величина наращивания суммы.

Рисунок 4.2 – Кривые роста инвестиционной суммы при различных количествах интервалов начисления в году (номинальная процентная ставка j = 200% годовых)

Аналогично случаю простых процентов, полученные формулы можно преобразовать, выражая одни величины через другие в зависимости от того, что известно, а что требуется найти.

Так, из формулы (4.16) получаем величину первоначальной денежной суммы по известной наращенной (дисконтирование):

. (4.25)

Из формулы (4.25) следует, что текущий денежный эквивалент (Р) будущей денежной суммы (S) тем ниже, чем отдаленнее срок ее получения (n) и чем выше норма доходности (ic).

Из формулы (4.16) имеем

. (4.26)

Из формулы (4.21)

. (4.27)

Применяя опцию логарифмирования к формулам (4.16) и (4.21) имеем:

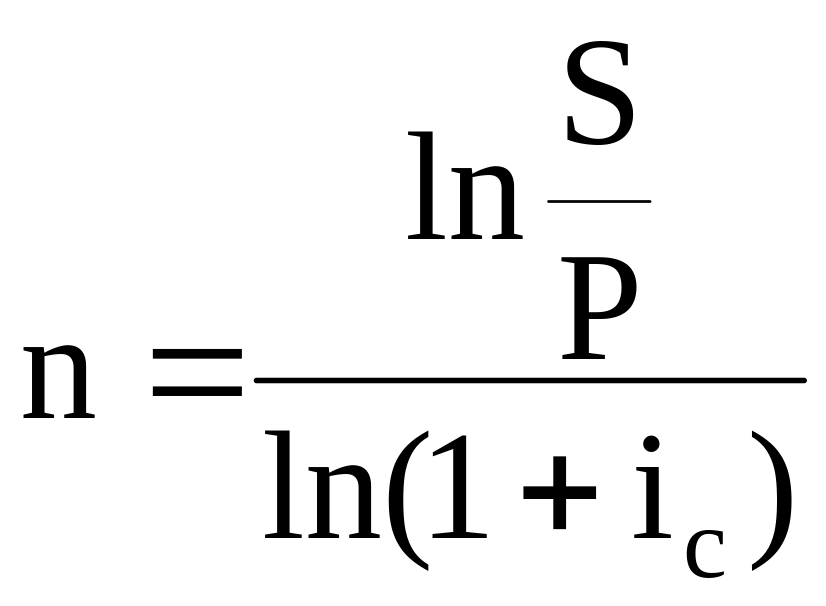, (4.28)

. (4.29)

Существует несколько правил, позволяющих быстро рассчитать срок удвоения первоначальной денежной суммы, зная конкретную процентную ставку.

1 Правило «70» .

2 Правило «69» .

Эти правила дают относительно точный результат для <100%, чем больше будет и превышать 100%, тем больше будет погрешность вычислений . При этом срок удвоения, полученный по правилам “70” или “69”, будет больше, чем в действительности.

Простые и сложные учетные ставки процентов

При антисипативном способе начисления процентов сумма получаемого дохода рассчитывается исходя из суммы, получаемой по прошествии интервала начисления, то есть из наращенной суммы. Эта сумма и считается величиной получаемого кредита. Так как в этом случае проценты начисляются в начале каждого интервала начисления, то заемщик получает эту сумму за вычетом процентных денег. Такая операция называется дисконтированием по учетной ставке.

Дисконтом называется доход, полученный по учетной ставке, то есть разница между размером кредита и непосредственно выдаваемой суммой.

Введем обозначения:

d (%), d – простая годовая учетная ставка;

D_г – сумма процентных денег, выплачиваемых за год;

D – общая сумма процентных денег;

S – сумма, которая должна быть возвращена;

Р – сумма, получаемая заемщиком.

Тогда, согласно определениям, имеем следующие формулы:

1. d = D_г/S d(%) = (D_г/S)100% (4.30)

2. D_г = Sd (4.31)

3. D = nD_г = ndS (4.32)

4. P = S-D = S(1- nd) = S(1-(/k)d) (4.33)

5. S = P/(1-nd) = P/(1-(/k)d) (4.34)

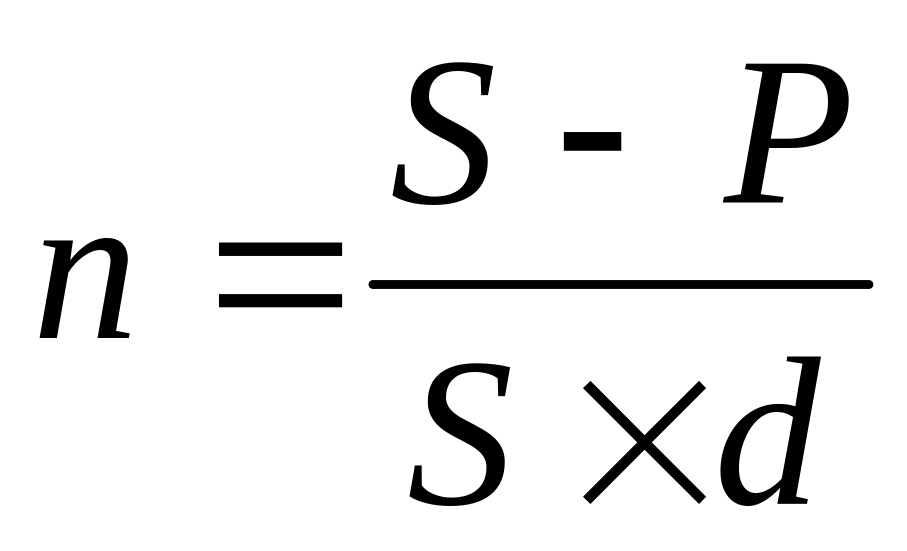6. (4.35)

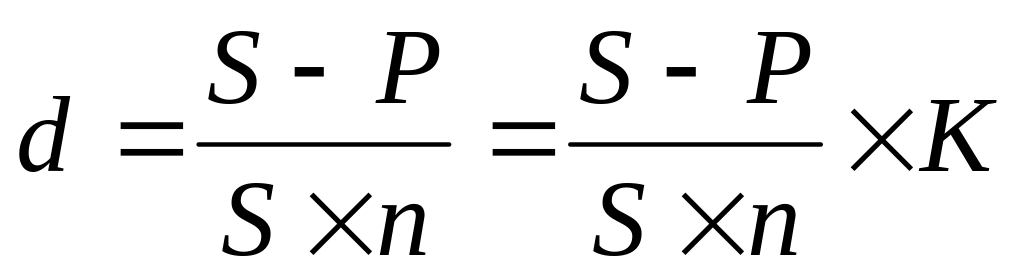7. (4.36)

На практике учетные ставки применяются, как правило, при покупке векселей и других денежных обязательств.

Антисипативный способ начисления сложных процентов

Введем обозначения:

сложная учетная годовая ставка;

коэффициент (множитель) наращения для сложной учетной ставки;

номинальная годовая учетная ставка.

По прошествии 1-го года наращенная сумма S в соответствии с формулой (4.34) составит

,

еще через год эта формула будет применяться уже к сумме S1 и

….

По прошествии n лет наращенная сумма составит

. (4.37)

Множитель наращения

. (4.38)

Формулы (4.16) и (4.37) показывают, что при равенстве ссудного процента и учетного процента наращивание первоначальной суммы во втором случае (антисипативный метод) идет быстрее. Поэтому в литературе можно встретить утверждение, что декурсивный способ начисления процентов (4.16) более выгоден для заемщика, т.е. заемщик получит больше, а антисипативный метод (4.37) более выгоден для кредитора. Для небольших процентных ставок расхождение между наращенными суммами не столь значительно (рис.4.3).

Но с ростом процентной ставки разница в величине наращенной суммы становится огромной (рис.4.4), и сравнение двух методов с точки зрения выгодности утрачивает смысл.

Из формулы (4.37) следует, что для периодов начисления, превышающих 1 год (n>1), учетная ставка может принимать значения только строго меньше 100%, иначе величины S и P не будут иметь смысла, становясь бесконечными или даже отрицательными.

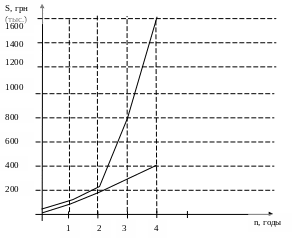
Рисунок 4.3 – Декурсивный (нижняя кривая) и антисипативный (верхняя кривая) способы начисления сложных процентов при =

Рисунок 4.4 – Декурсивный метод и антисипативный методы начисления сложных процентов при =

Для периода начисления, не являющегося целым числом, имеем:

, (4.39)

;

где – целое число лет начисления;

– оставшаяся дробная часть периода начисления.

При учетной ставке, изменяющейся в течение срока ссуды, наращения суммы рассчитывается:

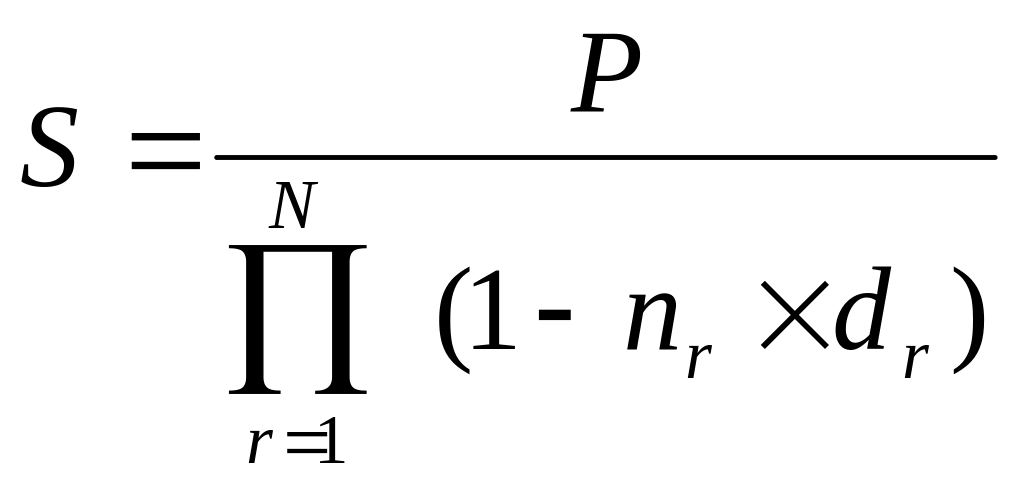, (4.40)

где n₁, n₂, …, n_N – продолжительность интервала начисления в годах;

d₁, d₂, …, d_N – учетные ставки, соответствующие данным интервалам.

При начислении процентов m раз в году:

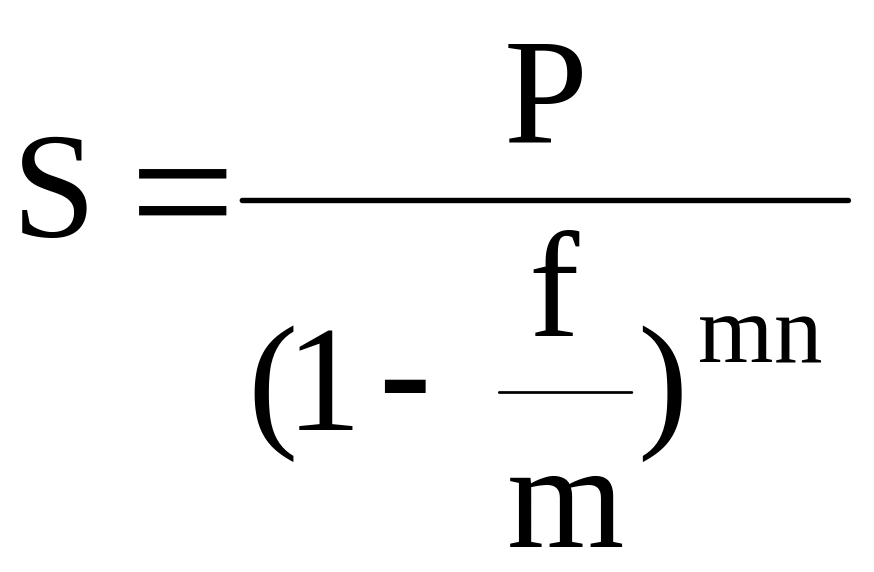, (4.41)

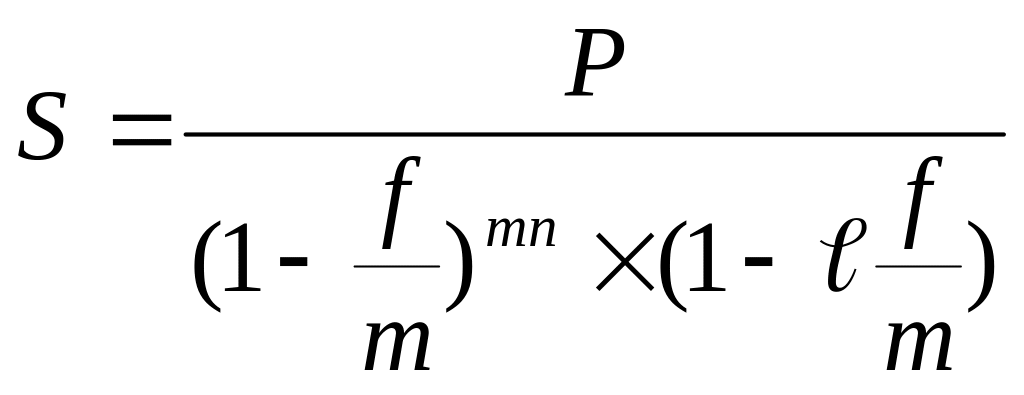. (4.42)

где mn – целое число интервалов начисления за весь период начисления;

- оставшаяся дробная часть интервала начисления.

При непрерывном начислении процентов S рассчитывается по формуле

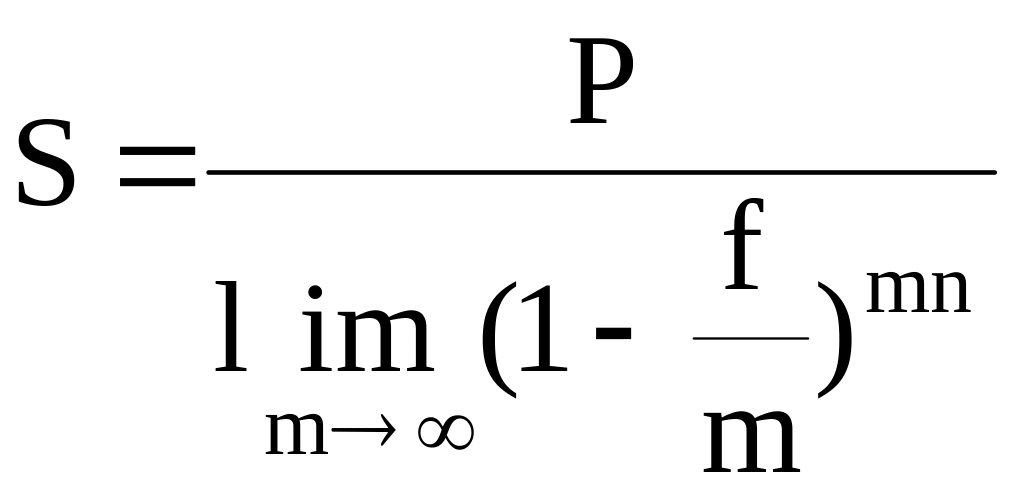. (4.43)

Из полученных формул путем преобразований получим формулы для определения первоначальной суммы Р, срока начисления n и величины учетной ставки dc:

, (4.44)

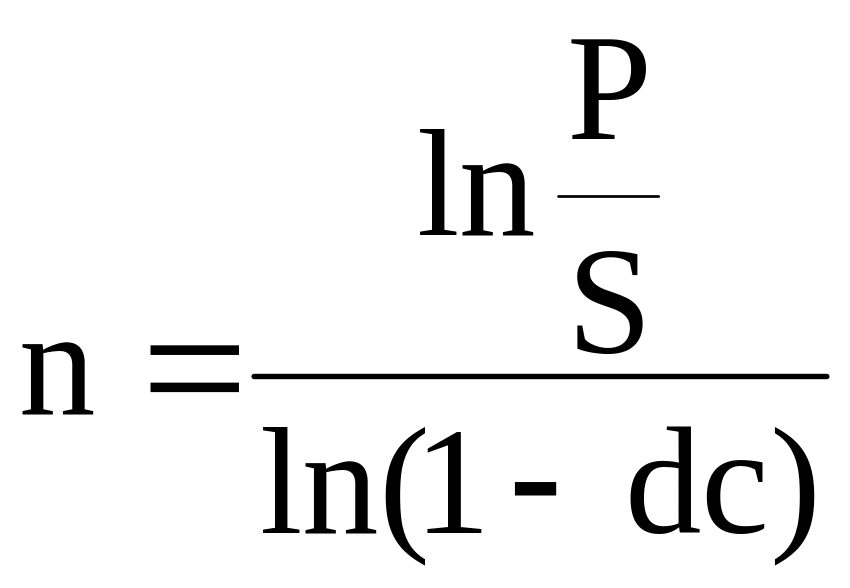, (4.45)

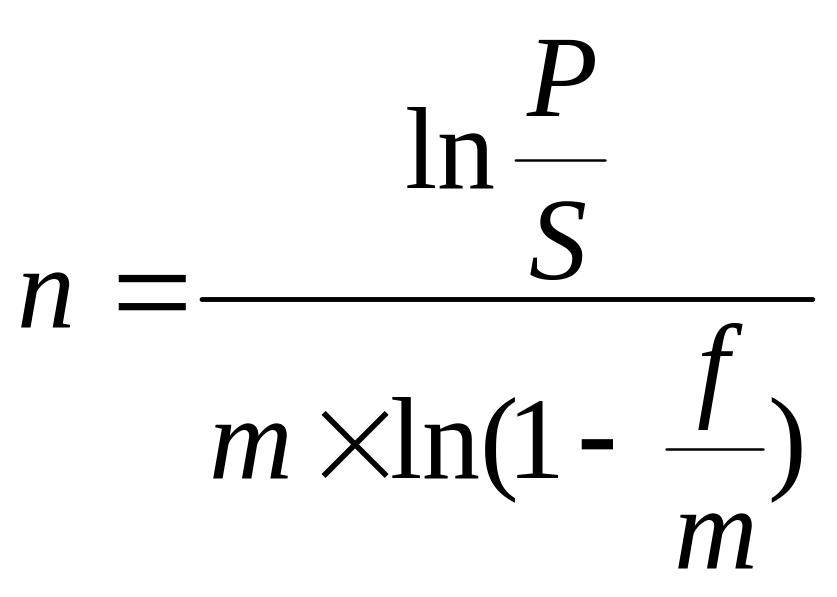, (4.46)

, (4.47)

. (4.48)

Эквивалентность процентных ставок различного вида

Эквивалентные процентные ставки – это такие процентные ставки различного вида, применение которых при одинаковых начальных условиях дает одинаковые финансовые результаты.

Эквивалентные процентные ставки необходимо знать в тех случаях, когда существует возможность выбора условий финансовой операции и требуется инструмент для корректного сравнения различных процентных ставок.

Для нахождения эквивалентных процентных ставок используют уравнения эквивалентности, сущность составления которых заключается в следующем:

• выбирается величина, которую можно рассчитать при использовании разных процентных ставок. Обычно в качестве такой величины рассматривается наращенная сумма S;

• на основе равенства двух выражений для данной величины, составляется уравнение эквивалентности, из которого путем соответствующих преобразований получается соотношение, выражающее зависимость между процентными ставками различного вида.

Рассмотрим случай, когда все условия финансовой операции совпадают, т.е. первоначальный капитал Р, временная база К, метод расчета процентов (точный или обыкновенный) и период начисления n одинаковы.

Повторим формулы для определения наращения суммы S при различных способах начисления процентов:

(4.7)

S = P/(1-nd) (4.34)

S = P(1+i_c)ⁿ (4.17)

(4.41)

(4.43)

Приравнивая эти формулы попарно, можно получить соотношение, выражающее зависимость между любыми двумя различными процентными ставками. Приравнивая соотношения (4.7) и (4.34), получаем:

,

, (4.49)

. (4.50)

Приравнивая формулы (4.7) и (4.17), получаем соответствие между простой и сложной ставками ссудных процентов:

,

, (4.51)

. (4.52)

Из формул (4.7) и (4.41) получаем взаимосвязь между простой ставкой ссудных процентов и номинальной годовой ставкой ссудных процентов j при условии начисления процентов несколько раз в году (m раз).

,

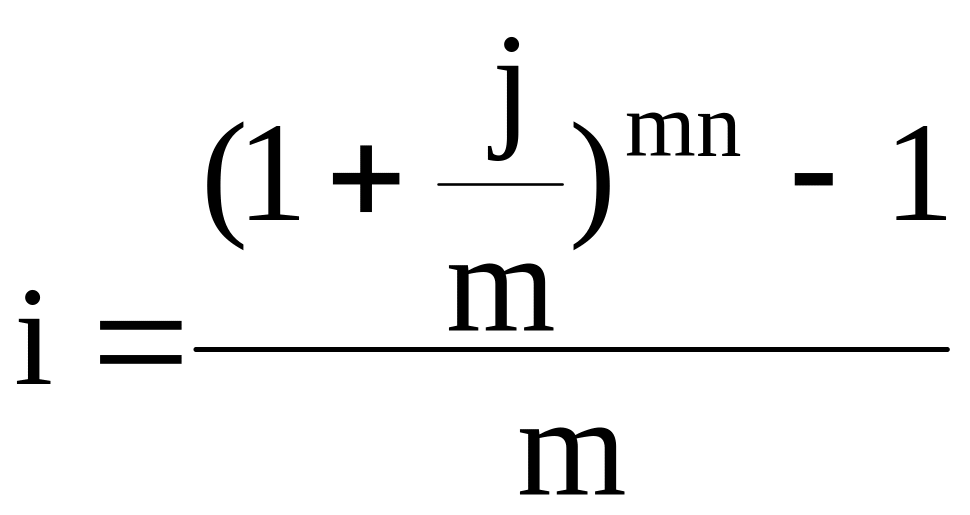, (4.53)

. (4.54)

Для различных случаев сложных процентов получаем уравнение эквивалентности, приравнивая формулы (4.17) и (4.41):

,

, (4.55)

. (4.56)

Полученная по формуле (4.55) годовая ставка сложных процентов, эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов, которую необходимо знать для того, чтобы оценить реализацию доходной финансовой операции или сравнить процентные ставки в случае, когда используются различные интервалы начисления.

Очевидно, что значение эффективной процентной ставки больше значения номинальной (ic>j) и совпадает при m = 1.

Из формул (4.17) и (4.37) имеем соотношение между сложной ставкой ссудных процентов ic и сложной учетной ставкой dc.

,

, (4.57)

. (4.58)

Анализ полученных формул позволяет сделать следующие выводы:

1 Эквивалентность различных процентных ставок никогда не зависит от величины первоначальной суммы Р (для данного рассматриваемого случая, когда первоначальная сумма Р предполагается одинаковой).

2 Эквивалентность процентных ставок всегда зависит от продолжительности периода начисления за исключением случая эквивалентности между сложными процентными ставками разного вида или если период начисления один и тот же.

Концепция и методический инструментарий учета фактора инфляции

В финансовом менеджменте постоянно приходится считаться с фактором инфляции, которая с течением времени обесценивает стоимость находящихся в обращении денежных средств.

Влияние инфляции сказывается на многих аспектах финансовой деятельности предприятия. В процессе инфляции происходит относительное занижение стоимости отдельных материальных активов, используемых предприятием (основных средств, запасов товарно-материальных ценностей и т.п.); снижение реальной стоимости денежных и других его финансовых активов (дебиторской задолженности, нераспределенной прибыли, инструментов финансового инвестирования и т.п.); занижение себестоимости производства продукции, вызывающее искусственный рост суммы прибыли и приводящее к росту налоговых отчислений с нее; падение реального уровня предстоящих доходов предприятия и т.п. Особенно сильно фактор инфляции сказывается на проведении долгосрочных финансовых операций предприятия.

Стабильность проявления фактора инфляции и его активное воздействие на результаты финансовой деятельности предприятия определяют необходимость постоянного учета влияния этого фактора в процессе финансового менеджмента.

Концепция учета влияния фактора инфляции в управлении различными аспектами финансовой деятельности предприятия заключается в необходимости реального отражения стоимости его активов и денежных потоков, а также в обеспечении возмещения потерь доходов, вызываемых инфляционными процессами, при осуществлении различных финансовых операций.

Реализация этой концепции в практике финансового менеджмента и использование соответствующего её методического инструментария требуют знания связанных с ней следующих базовых понятий.

Инфляция – процесс постоянного превышения темпов роста денежной массы над товарной, в результате чего происходит переполнение каналов обращения деньгами, сопровождающееся их обесцениванием и ростом цен.

Темп инфляции – показатель, характеризующий размер обесценивания денег в определенном периоде, выраженный приростом среднего уровня цен в процентах к их номиналу на начало периода.

Индекс инфляции – показатель, характеризующий общий рост уровня цен в определенном периоде, определяемый путем суммирования базового их уровня на начало периода и темпа инфляции в рассматриваемом периоде.

Инфляционная премия – дополнительный доход, выплачиваемый кредитору или инвестору с целью возмещения финансовых потерь от обесценения денег в связи с инфляцией.

1 Методический инструментарий прогнозирования годового темпа и индекса инфляции основывается на ожидаемых среднемесячных её темпах.

При прогнозировании годового темпа инфляции используется следующая формула:

, (4.59)

где – прогнозируемый годовой темп инфляции, выраженный десятичной дробью;

– ожидаемый среднемесячный темп инфляции в предстоящем периоде, выраженный десятичной дробью.

По этой формуле может быть рассчитан не только прогнозируемый годовой темп инфляции, но значение этого показателя на конец любого месяца предстоящего года.

При прогнозировании годового индекса инфляции используется следующая формула:

(4.60)

или

, (4.61)

где – прогнозируемый годовой индекс инфляции;

– прогнозируемый годовой темп инфляции;

– ожидаемый среднемесячный темп инфляции.

2 Методический инструментарий формирования реальной процентной ставки с учетом фактора инфляции основывается на прогнозируемом номинальном её уровне, на финансовом рынке и результатах прогноза годовых темпов инфляции. В основе расчета реальной процентной ставки лежит модель Фишера, которая имеет следующий вид:

, (4.62)

где – реальная процентная ставка;

– номинальная процентная ставка;

– темп инфляции.

3 Методический инструментарий оценки стоимости денежных средств с учётом фактора инфляции.

При оценке будущей стоимости денежных средств с учётом фактора инфляции используется формула-модификация рассмотренной ранее модели Фишера

, (4.63)

где – номинальная будущая стоимость вклада, учитывающая фактор инфляции;

– первоначальная сумма вклада;

– реальная процентная ставка;

– прогнозируемый темп инфляции;

– количество интервалов, по которым осуществляется каждый процентный платёж, в общем периоде времени.

При оценке настоящей стоимости денежных средств с учётом фактора инфляции используется формула

, (4.64)

где – реальная настоящая сумма вклада, учитывающая фактор инфляции.

4 Методический инструментарий формирования необходимого уровня доходности финансовых операций с учётом фактора инфляции.

При определении необходимого размера инфляционной премии используется формула:

, (4.65)

где – сумма инфляционной премии в определённом периоде;

– первоначальная стоимость денежных средств;

– темп инфляции.

При определении общей суммы необходимого дохода по финансовой операции с учётом фактора инфляции используется формула

, (4.66)

где – общая номинальная сумма необходимого дохода по финансовой операции;

– реальная сумма необходимого дохода по финансовой операции, исчисленная по простым или сложным процентам с использованием реальной процентной ставки;

– сумма инфляционной премии в определённом периоде.

При определении необходимого уровня доходности финансовых операций с учётом фактора инфляции используется формула

, (4.67)

где – необходимый уровень доходности финансовых операций с учётом фактора инфляции;

– общая номинальная сумма необходимого дохода по финансовой операции;

– реальная сумма необходимого дохода по финансовой операции.

Следует отметить, что прогнозирование темпов инфляции представляет собой довольно сложный и трудоёмкий вероятностный процесс, в значительной степени подверженный влиянию субъективных факторов. Поэтому в практике финансового менеджмента может быть использован более простой способ учёта фактора инфляции. В этих целях стоимость денежных средств пересчитывается заранее из национальной валюты в одну из «сильных» свободно конвертируемых валют по курсу на момент проведения расчётов. Процесс наращения или дисконтирования стоимости осуществляется затем по реальной процентной ставке. Такой способ позволяет вообще исключить из расчётов фактор инфляции внутри страны.