Практична робота №5

Побудова перевіряючих тестів для комбінаційних логічних схем.

Дослідження особливостей побудови тестів

із застосуванням d - алгоритму.

Мета: Навчитися формувати тести для діагностування комбінаційних схем із застосуванням d –алгоритму.

Теоретичні відомості

Метод активізації багатомірного шляху (d-алгоритм), запропонований К.Ф.Ротом, є першим алгоритмічним методом побудови тестів для беззалишкових комбінаційних схем. Іншими словами, цей алгоритм гарантує знаходження тесту для заданої несправності, якщо такий тест існує.

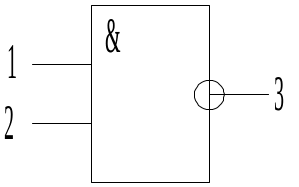
Алгоритм Рота оснований на застосуванні кубічного опису булевих функцій, що є однією з можливих форм їхнього завдання. Серед кубічних представлень булевих функцій, що використовуються у зазначеному алгоритмі, першими є так звані сингулярні куби, сукупністю яких є сингулярні покриття схеми, що реалізують булеву функцію. Для задання сингулярних кубів використовуються символи 0, 1, X, де Х означає, що змінна по даній координаті може приймати як нульове, так і одиничне значення. Як приклад на рис.5.1 приведена множина сингулярних кубів для елементів "2ТА-НІ" та "2АБО-НІ".

1 2 3 1 1 0 0 Х 1 Х 0 1

1 2 3 0 0 1 1 Х 0 Х 1 0

Рис.2.1.Приклади вироджених покриттів для елементів "2ТА-НІ" і "2АБО-НІ".

Розглянуті сингулярні куби використовуються для отримання d-кубів, при заданні яких застосовуються символи 0, 1, , . Символ може позначати як 0 так і 1, а приймає значення, протилежне символу . Для конкретної цифрової схеми всі символи приймають те саме значення 0 чи 1, а - відповідно 1 чи 0.

-куб, що описує поводження цифрової схеми, виходить у результаті виконання покоординатної операції перетинання двох сингулярних кубів із сингулярного покриття схеми, що мають різне значення по вихідній координаті, на підставі наступних співвідношень:

00=0	0X=0	X0=0
1  1=1	1X=1	X1=l
ХХ=Х	l0=	0l=

Так, наприклад, на підставі кубів та із сингулярного покриття елемента "2ТА-НІ" в результаті їх по координатного перетинання отримаємо -куб .

Для опису існування заданої несправності використовуються так звані примітивні -куби несправності, що складаються з вхідного набору, що дозволяє спостерігати несправність по виходу елемента, і символу чи у вихідній координаті. Для прикладу, приведеного на рис. 4.1, і несправності по виходу елемента "2АБО-НІ" відповідний примітивний -куб буде мати вигляд:

1	2	5
0	0

В даному випадку означає, що в справному стані по вихідній координаті повинний бути символ 1, а в несправному - 0. У той же час для кубів:

1	2	5
1	Х
Х	1

що описують поведінку елемента "2АБО-НІ" у випадку несправності 1 (“константна 1”) по його виходу, означає, що в справному стані на його виході повинний бути символ 0, а в несправному - 1.

- куб несправності порівняно легко будується для одного елемента схеми, на вході або на виході якого є присутня константна несправність. Однак основною задачею -алгоритму є побудова - куба несправності всієї розглянутої схеми. Для цієї мети використовується операція -перетину, введена Ротом з метою формалізації процедури активізації багатомірного шляху. Покоординатна операція -перетину ( ) визначається згідно табл.5.1.

Таблиця 5.1 Правила виконання операції -перетину

	0	1			Х
0	0				0
1		1			1
				
			
X	0	1			Х

Якщо при перетині кубів виникає хоча б один символ , то це вказує на протиріччя, що виникає на даній лінії внаслідок різних умов.

Безпосередньо -алгоритм складається з наступних основних етапів:

1. Вибирається примітивний -куб заданої несправності елемента цифрової схеми.

2. Активізуються можливі шляхи від елемента, що містить несправність, до виходу схеми. При цьому застосовується операція -перетину куба несправності з -кубами елементів, послідовно з'єднаних між вихідним несправним елементом і виходами схеми. У результаті початкового перетинання -куба несправності з -кубом наступного елемента отримується -куб заданої несправності, що описує поводження схеми з двох елементів.

Послідовність перетинань -кубів несправності з -кубами елементів, що знаходяться на шляхах транспортування несправності, часто називають процедурою -проходу. Закінчується -прохід тільки тоді, коли хоча б на одній з вихідних координат не буде отримане значення символу чи .

3. Виконується зворотна фаза як процедура послідовного перетинання отриманого -куба заданої несправності, що описує поводження несправності елемента, і елементів, що лежать на шляхах транспортування несправності із сингулярними кубами інших елементів.

Практичне застосування -алгоритму розглянемо на прикладі цифрової схеми, приведеної на рис.4.1, у випадку несправності .

Спочатку побудуємо множину сингулярних кубів та -кубів для елементів "2АБО-НІ" і "4АБО-НІ" і примітивні -куби несправності елемента "2АБО-НІ", що необхідні для реалізації -алгоритму.

Відповідно будемо мати наступні сингулярні куби:

"2АБО-НІ" 1 2 3 0 0 1 1 Х 0 Х 1 0

"4АБО-НІ" 1 2 3 4 5 0 0 0 0 1 1 Х Х Х 0 Х 1 Х Х 0 Х Х 1 Х 0 Х Х Х 1 0

Відповідні -куби:

"2АБО-НІ" 1 2 3 0 0

"4АБО-НІ" 1 2 3 4 5 0 0 0 0 0 0 0 0 0 0 0 0

примітивний -куб несправності:

"2АБО-НІ" 1 2 3 0 0 1 Х Х 1

або

"2АБО-НІ" 1 2 3 0 0 0 1 1 0 1 1

Використовуючи отримані множини кубів, побудуємо тестовий набір для виявлення несправності комбінаційної схеми, приведеної на рис.4.1. Для цього спочатку з множини примітивних -кубів несправності елемента 2 ("2АБО-НІ") виберемо куб , що описує несправне поводження елемента при . Далі на першому кроці -проходу виконаємо процедуру -перетину -куба несправності з -кубом , що описує елемент 5, і відповідно отримаємо:

	1	2	3	4	5	6	7	8	9	10	11	12
	Х	0	0	Х	Х		Х	Х	Х	Х	Х	Х
	0	Х	Х	Х	Х		Х	Х		Х	Х	Х
	0	0	0	Х	Х		Х	Х		Х	Х	Х

(цифри 1-12 – номера полюсів схеми).

З огляду на те, що несправність може транспортуватися через елементи 5 і 6 схеми одночасно, перетнемо отриманий куб з -кубом, що описує елемент 6:

	1	2	3	4	5	6	7	8	9	10	11	12
	0	0	0	Х	Х		Х	Х		Х	Х	Х
	Х	Х	Х	0	Х		Х	Х	Х		Х	Х
	0	0	0	0	Х		Х	Х			Х	Х

Куб перетинається з -кубом елемента "4АБО-НІ":

	1	2	3	4	5	6	7	8	9	10	11	12
	0	0	0	0	Х		Х	Х			Х	Х
	Х	Х	Х	Х	Х	Х	Х	Х			0
	0	0	0	0	Х		Х	0			0

Поява символу у вихідній координаті свідчить про закінчення -проходу. Зворотна фаза -алгоритму для розглянутого прикладу буде складатися в послідовному перетинанні куба із сингулярними кубами елементів 4 і 7. В результаті отримаємо:

	1	2	3	4	5	6	7	8	9	10	11	12
	0	0	0	0	Х		Х	0			0
	Х	Х	Х	Х	1	Х	Х	0	Х	Х	Х	Х
	0	0	0	0	1		Х	0			0
	Х	Х	Х	Х	Х	Х	1	Х	Х	Х	0	Х
	0	0	0	0	1		1	0			0

Таким чином, остаточно отримаємо куб , який показує, що при подачі на входи схеми (рис. 4.1) набору і наявності несправності на полюсі 6 схеми формується значення нуля, що буде зафіксовано і на вихідному полюсі 12 схеми. При відсутності зазначеної несправності на полюсі 12 схеми буде формуватися значення одиниці. Таким чином, вхідний набір 0000 є тестом для несправності .

Розглянутий -алгоритм дозволяє побудувати тест для кожної несправності комбінаційної цифрової схеми, якщо такий тест існує. Крім того, даний алгоритм здатний ідентифікувати наявність надлишковості в цифровій схемі, вимагає порівняно невеликого обсягу пам'яті і відрізняється невисокою трудомісткістю, що дозволяє широко використовувати його в системах автоматичної генерації тестів.

Для спрщення автоматизації розглянутого методу необхідно додатково будувати допоміжні таблиці. Розглянемо ще один приклад генерації тестів за допомогою -алгоритму для комбінаційної схеми рис. 5.1, в якому використовується дещо інший підхід.

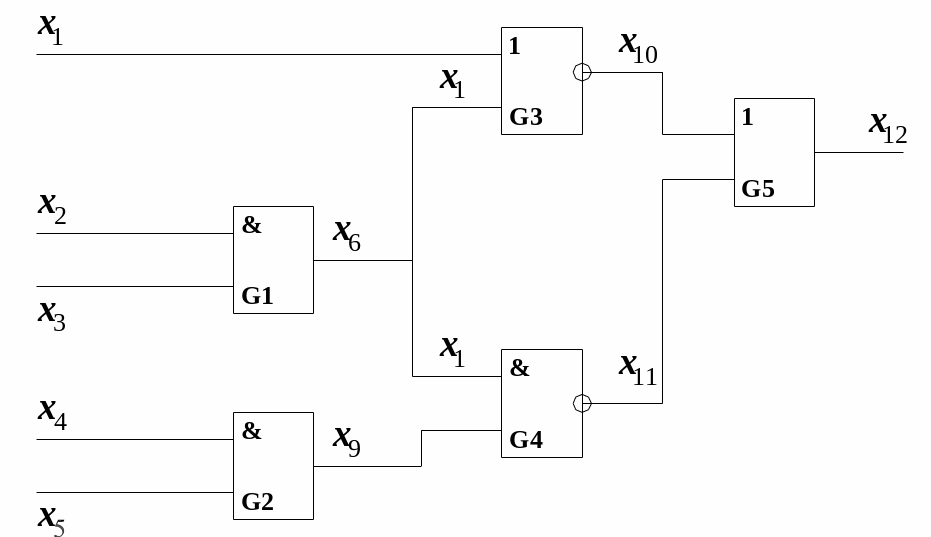
Рис. 5.1. Комбінаційна схема.

Таблиця 5.2. містить ( )-куби для схеми зображеної на рис.5.1. Порожні клітинки відповідають невизначеним значенням Х. Таблиця 5.3. містить 0 (1)-куби.

Таблиця 5.2. ( )-куби для схеми зображеної на рис.5.1.

Лінії Куб		X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	X11	X12
1	2	3	4	5	6	7	8	9	10	11	12	13	14
				1
			1
				1
1	2	3	4	5	6	7	8	9	10	11	12	13	14
			1
						1
					1
						1
					1
								0
		0
								0
		0
										1
									1
										1
									1
												0
											0
												0
											0

1	2	3	4	5	6	7	8	9	10	11	12	13	14
Розгал.

Таблиця 5.3. 0(1) – куби покриття схеми рис.5.1.

Лінії Куб		X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	X11	X12
1	2	3	4	5	6	7	8	9	10	11	12	13	14
	С1		0	Х			0
	С2		Х	0			0
	С3						0
	С4						0
	С5		1	1			1
	С6				0	Х				0
	С7				Х	0				0
	С8									0
	С9									0
	С10				1	1				1
	С11	1						Х			0
	С12	Х						1			0
	С13										0
	С14										0
	С15	0						0			1
	С16								1	1		0
	С17								0	Х		1
	С18								Х	0		1
	С19											1
	С20											1
	С21										0	0	0
	С22										1	Х	1
	С23										Х	1	1
	С24												1
	С25												1

Крім цих таблиць використовується куб для поточних значень ліній схеми та кілька стеків. Спочатку всім рядкам куба присвоюється невизначені значення Х. Далі в вноситься простий куб відповідної несправності. Далі виконується розповсюдження до одного з виходів схеми. Воно виконується шляхом обрання послідовника несправного логічного елемента та перетину з одним з його -кубів. При виконанні операції -перетину проводять вибір одного з або -кубів, а решта варіантів зберігаються в стеку.

За цією послідовністю кроків можна сформулювати алгоритм у вигляді псевдокоду:

-алгоритм (несправність )

{

Вибір простого -куба несправності ;

Занесення елементів наступників в границю;

- розповсюдження ();

Довизначення ();

Return();

}

- розповсюдження ()

// активізує шляхи з , -значеннями від несправності до

// зовнішнього виходу

{

while (є необроблені елементи в -границі)

{

Вибір наступного необробленого елементу з -границі;

while (є необроблені елементи наступники)

{

Вибір слідуючого елемента-наступника;

Вибір -куба елемента наступника;

-перетин обраного -куба з поточним тест-кубом ;

if (перетин пустий або не визначений) continue;

// перехід на кінець циклу

if (всі -куби елемента використовувались і не дали результата) break;

if (перетин всіх -кубів успішний)

{

Занесення елементів наступників значень в границю;

Збереження стану алгоритма в стеку;

Break;

}

else if ( перетин -куба з тестовим пустий) повернення();

else if (протиріччя при виконанні опереації перетину) break;

}

if (жоден з варіантів не дав -розповсюдження)

повернення();

}

return;

}

Довизначення ()

// дає значення зовнішніх входів, що відповідають умовам

// -розповсюдження

{

J-координати тестового куба з визначиними значеннями 0,1;

if (J містить тільки зовнішні входи)

тест побудовано, останов;

for (кожного не підтвердженного сигналу в G)

{

вибір 0,1 сигналу z з J з найбільшим рангом;

if (входи елемента з виходом z всі рівні або)

break;

while (є необроблені 0(1)-куби логічного елемента z)

{

вибір наступного необробленого 0(1) куба елемента z;

if (немає необроблених 0(1) кубів)

{

if (немає вибору в стеці імплікації) stop;

несправність надмірна;

else if (є альтернативний вибір)

then вивільнення зі стека альтернативного значення;

else

{

повернення();

-розповсюдження();

}

}

if (0(1)-куб перетинається з z) видалення z з J та занесення в J-границю значень входів z;

break;

if (перетин пустий) відмітка поточного 0(1)-куба як відпрацьованого;

}

}

return;

}

Повернення()

{

if (зовнішній вихід міститься в -границі)

Довизначення();

else вивільнення зі стеку імплікації альтернативного значення);

if (немає варіантів в стеці імплікації) stop;

несправність надмірна;

else return;

}

Розглянемо застусування -алгоритму для побудови теста несправності схеми зображеної на рис. 5.1.

При ініціалізації отримуємо куб , що наведений в таблиці 5.4. Елементи та однаково наближені до виходу, -границя містить елементи . Обираємо для -розповсюдження елемент . Перетинаючи -куб вузла розгалуження елемента з кубом , як це зображено в таблиці 5.4 б), в), отримуємо куб . Поповнюємо -границю . Далі обираємо -куб елемента та перетинаючи його з , отримуємо , як показано в таблиці 5.4. г). Так як ми досягнули зовнішнього виходу, то етап -розповсюдження завершено. Далі слід виконати процедуру довизначення. Стек довизначення повинен містити на даний момент елементи . Обираємо 1-куб елемента та виконуючи його перетин з кубом , як наведено в таблиці 5.4. д), отримуємо . Аналогічно довизначаємо входи (табл. 5.4 е). В результаті отримуємо тест .

Таблиця 5.4. Реалізація -алгоритму

	1	2	3	4	5	6	7	8	9	10	11	12
	Х	1	1	Х	Х		Х	Х	Х	Х	Х	Х

а)

Х

1

1

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

1

1

Х

Х

Х

Х

Х

Х

б)

Х

1

1

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

1

Х

Х

Х

1

1

Х

Х

1

Х

Х

в)

Х

1

1

Х

Х

1

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

Х

0

Х

1

1

Х

Х

1

0

г)

	Х	1	1	Х	Х				1	0
	Х	Х	Х	1	1	Х	Х	Х	1	Х	Х	Х
	Х	1	1	1	1				1	0

д)

	Х	1	1	1	1				1	0
	1	Х	Х	Х	Х	Х	Х	Х	Х	0	Х	Х
	1	1	1	1	1				1	0

е)

Слід зазаначити, що для схем, що містять багато єлементів "додавання за модулем 2" (схем контроля парності) процедура - розповсюдження виконується достатньо легко, однак при виконанні процедури довизначення часто виникають протиріччя і для таких схем - алгоритм вимагає значних витрат часу. Для цього класу схем було розроблено метод PODEM, який добре зарекомендував себе і для інших схем.