Тема № 2. Графический метод решения задач линейного программиро­вания.

Каноническая и стандартная формы записи задачи линейного программирования. Гео­метрическое изображение системы ограничений. Линия уровня линей­ной функции. Этапы решения задачи.

Содержание основных понятий темы

Каноническая задача линейного программирования помимо дополнительных (тривиальных) ограничений включает систему ограничений, состоящую только из уравнений

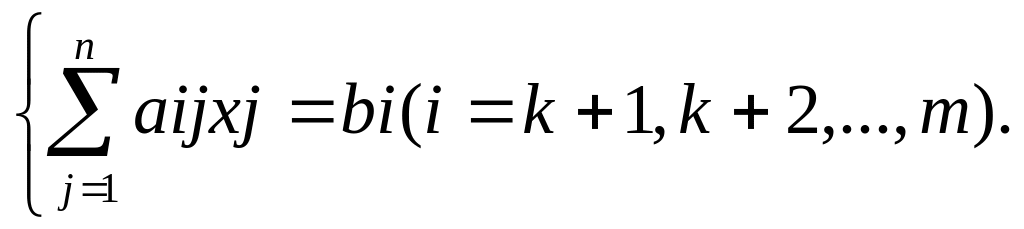
Стандартная задача линейного программирования помимо дополнительных (тривиальных) ограничений включает в качестве ограничений только неравенства

Графический метод решения задач линейного программирования применяется только для случая, когда задача имеет две независимые переменные.

Задача линейного программирования для двух переменных имеет вид:

Графическим решением уравнений, входящих в систему ограничений, являются уравнения прямых, которые можно записать в виде

Множеством решений неравенств с двумя переменными является одна из двух плоскостей, на которые вся плоскость делится прямой включая и эту прямую, а другая полуплоскость с этой же прямой является множеством решений неравенства

Задача 1.

Построить график множества решений следующий неравенств:

а) б)

Решение.

Множества решений приведенных неравенств есть полуплоскость.

а) Границей первой полуплоскости является прямая .

Представим уравнение этой прямой в виде . Ее график показан на рис.1.

Для определения искомой полуплоскости зададим произвольную контрольную точку, не лежащую на построенной прямой. Например, точку с координатами (0,0). Подставив эти координаты в неравенство видим, что оно не выполняется, так как 8 0. Поэтому искомой является верхняя полуплоскость;

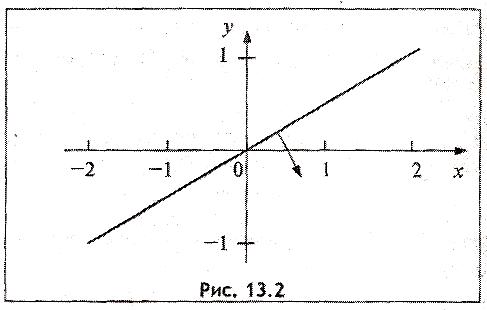
б) границей второй полуплоскости является прямая . Представим это уравнение в виде . График исследуемой прямой показан на рис.2.

В данном случае точка с координатами (0,0) лежит на этой прямой. Поэтому выбираем точку с координатами (0,-1) и подставляем эти координаты в неравенство . Так как неравенство выполняется (4>0), то искомой является нижняя полуплоскость.

рис.2.

Выпуклое замкнутое множество точек плоскости имеющее конечное число угловых точек, называется выпуклым многоугольником, если оно ограниченное, и выпуклой мно­гоугольной областью, если оно неограниченное.

Множество решений совместной системы ли­нейных неравенств с двумя переменными

является выпуклым многоугольником (или выпуклой многоугольной областью).

Знаки некоторых или всех неравенств могут быть .

Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью ре­шения системы.

Область решений системы, удовлетворяющая условиям неотри­цательности ( ), называется областью допустимых решений.

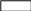
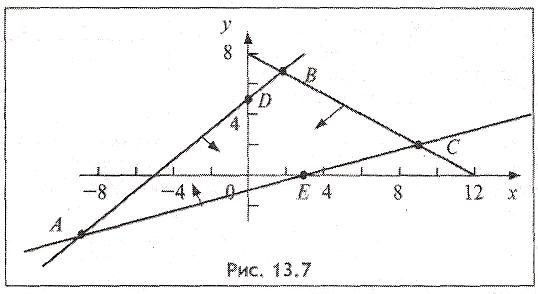
Задача 2.

Построить область решений и область допустимых решений системы неравенств:

и определить координаты угловых точек, области допустимых решений.

Решение.

Областью решений является треугольник АВС, представленный на рис. 3.

Сторона АВ треугольника, образованная границей первого неравенства системы, определяется уравнением прямой . Для нахождения искомой полуплоскости зададим контрольную точку с координатами (0,0). Подставим эти координаты в неравенство , видим, что оно выполняется, так как 0 20. Поэтому искомой является нижняя полуплоскость.

Сторона ВС треугольника, образованная границей второго неравенства системы, определяется, уравнением прямой . Для контрольной точки с координатами (0,0) неравенство выпол­няется, так как 0 24. Поэтому искомой также является нижняя полу­плоскость.

Сторона СD треугольника, образованная границей третьего нера­венства системы, определяется уравнением прямой . Для кон­трольной точки с координатами (0,0) неравенство выполня­ется, так как 0 3 . Поэтому искомой является верхняя полуплоскость.

Областью допустимых решений системы неравенств является пятиугольник ODBCE. Координаты угловых точек (вершин) этого пятиугольника находятся как координаты точек пересечения соответствующих пря­мых.

Например, точка В является точкой пересечения первой и второй прямых, т.е. её координаты являются решением системы двух уравнений:

Решив эту систему, получим . Аналогично находим

Если задача линейного программирования имеет оптимальное решение, то линейная функция принимает максимальное значение в одной из угловых точек многоугольника решений.

При решении задачи линейного программирования графическим способом используется линия уровня.

Линией уровня функции F(x,y) называется множество всех точек (x,y), в которых функция принимает постоянное значение a.

В случае линейной функции F= cx+dy все линии уровня являются прямыми, перпендикулярными общему вектору нормали , определяемому соотношением

где i, j - орты осей x, y соответственно. Координатами вектора являются коэффициенты целевой функции F(x,y).

Алгоритм графического метода решения задачи линейного программирования:

1. На координатной плоскости ХОУ построить область допустимых решений, соответствующую ограничениям (многоугольная область).

2. Если это множество равно нулю, то задача неразрешима.

3. Построить вектор а и провести линии уровня а = сх + dy . Прямую а, передвигать в направлении вектора а в случае максимизации функции (и в противоположном направлении в случае минимизации) пока она не покинет пределов многоугольной области. Предельная точка (или точки) области при этом движении является точкой максимума (минимума).

4. Если А - первая точка встречи прямой уровня с областью допустимых решений, F ( А) = а_о , то прямая F (х, у) = а при а < а_о не имеет общих точек с областью допустимых решений. Отсюда следует, что а_о является минимальным значением целевой функ­ции F = сх + dy в области допустимых решений.

5. Если А - последняя точка встречи прямой уровня с областью допустимых решений, то F ( А) = а_о является максимальным значе­нием целевой функции

F = сх + dy в области допустимых решений.

6. Найти координаты точки максимума, решив два уравнения прямых, получаемых из соответствующих ограничений и дающих при пересечении искомую точку.

7. Если окажется, что линия уровня параллельна одной из сто­рон области допустимых решений, то экстремум достигается во всех точках соответствующей стороны. Задача в этом случае будет иметь бесчисленное множество решений.

Задача 3 (задача об использовании ресурсов).

Предприятие выпускает сливочное и шоколадное мороженое. Для изготовления мо­роженого используются молоко и наполнители, расходы которых на 1 кг мороженого приведены в таблице. Маркетинговые исследования показали, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено что спрос на шоколадное мороженое не превышает 350 кг в сутки. Роз­ничная цена 1 кг сливочного мороженого равна 16 руб., шоколадного — 14 руб.

Какое количество мороженного каждого вида должно производиться, что бы доход от его реализации был максимальным?

Исходный продукт	Расход исходного продукта на 1 кг мороженого		Запас, кг
	Сливочное	Шоколадное
Молоко	0,8	0,5	400
Наполнители	0,4	0,8	365

Решение.

Если – суточный объем выпуска сливочного мороженого, а – суточный объем выпуска шоколадного мороженого, то задача линейного программирования можно записать в виде

при условиях

Область допустимых решении OABCDE представлена на рис. 4.

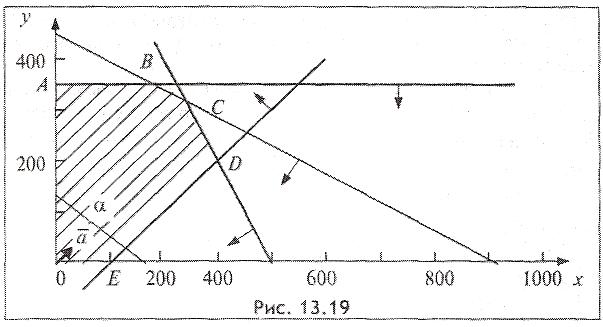
Действительно, соответствующие границы ограничений представлены уравнениями прямых:

Вектор и линии уровня определяются соотношениями

Перемещаем линию уровня по направлению вектора . Точкой выхода из области допустимых решении является точка С. Её координаты определяются как пересечение прямых:

Отсюда находим

руб.

Таким образом, для получения максимального дохода, равного 9200 руб., предприятие должно выпускать 312,5 кг сливочного мороженого и 300 кг шоколадного.

Самостоятельно решите следующие задачи:

1. Построить множество решений линейных неравенств:

1) , 2) , 3) ,

4) 5) 6)

2.2. Построить область решений и область допустимых решений следующих

систем неравенств:

1) 2) 3) 4)

2.3. Построить множества решений систем линейных неравенств и найти координаты их угловых точек.

1) 2) 3)

4) 5) 6)

7) 8) 9)

10) 11) 12)

2.4. Решить графически задачу линейного программирования:

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

2.5. Цех для изготовления двух видов продукций использует четыре груп­пы оборудования в количествах, указанных в таблице. Сколько единиц каж­дого вида продукции необходимо изготовить, чтобы получить максимальную прибыль?

Группа оборудования	Необходимое количество единиц оборудования на единицу продукции		Количество оборудования в группе
	I	II
А	2	2	12
В	1	2	8
С	4	0	16
D	0	4	12
Доход (тыс. руб. на 1 шт.)	2	4

2.6. Для производства кирпича двух марок (I, ΙΙ) предприятие использует оборудование трех видов (А, В, С), имеющееся в количествах соответственно не более 13, 9_, 8 у.е. Для производства одного кирпича I типа требуется 2 у.е. оборудования вида - А, 0 у.е. - вида В., 2 у.е. - вида С; для производства одного кирпича, II типа - 2, 3, 0 у.е. Известно, что от реализации одного кирпича I ти­па прибыль составляет 3 ден. ед_. ΙΙ типа - 4 ден. ед. Спланируйте производст­во так. чтобы получить наибольшую прибыль.

2.7. Фирма выпускает прогулочные и спортивные велосипеды. Ежемесяч­но сборочный цех способен собрать 600 прогулочных и 300 спортивных велосипедов, Готовая продукция проверяется на двух стендах; А и В, Каждый про­гулочным велосипед проверяется 0,3 ч на стенде А и 0,1 ч на стенде В, а каж­дый спортивный велосипед проверяется 0,7 ч на стенде А и 0,3 ч на стенде В. По технологическим причинам стенд А не может работать более 240 ч в ме­сяц, в стенд В - не более 120 ч в месяц. Каждый прогулочный велосипед приносит фирме доход 50 руб., а каждый спортивный велосипед - 90 руб. Сколь­ко прогулочных и сколько спортивных велосипедов должна ежемесячно вы­пускать фирма, чтобы ее прибыль была наибольшей?

2.8. На трёх станках обрабатываются два типа деталей, причем каждая проходит обработку на всех станках. Время обработки детали на каждом станке и время работы станка в течение цикла производства, а также прибыль от реализации одной детали приведены в таблице.

Виды Типы Станков дет.	Время обработки одной детали (ч)		Время работа станка в тече­нии цикла производства (ч)
	I	ΙΙ
1 - й станок	4	2	16
2 – й станок	1 3	6	30
3 – й станок	2	0	12
Прибыль от реализации одной детали (руб.)	3	4

Составьте план производства, обеспечивающий наибольшую прибыль.

2.9. Можно закупить корм двух видов (I и II). В каждой единице корма I ви­да содержатся 1 ед. витамина А, 2 ед. витамина В и нет витамина С; в каждой единице, корма II вида - 2 ед. витамина А, 1 ед. витамина В и 1 ед. витамина С. Животному необходимо дать в сутки не менее 10 ед. витамина А, 10 ед. витамина В и 4 ед. витамина С. Составить наиболее дешевый рацион питания животного. Если стоимость единицы корма I вида равна 2 ден. ед., а стоимость единицы корма II вида - 4 ден. ед.