МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

ВОСТОЧНОУКРАИНСКОГО НАЦИОНАЛЬНОГО УНИВЕРСИТЕТА

имени ВЛАДИМИРА ДАЛЯ

( г.Северодонецк )

Кафедра высшей и прикладной математики

БОГДАНОВ А.Е.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к самостоятельной работе

по дисциплине

“ДИСКРЕТНАЯ МАТЕМАТИКА “.

Для студентов дневной и заочной форм обучения

направления подготовки 6.050102

“Компьютерная инженерия”

УТВЕРЖДЕНО

на заседании кафедры

высшей и прикладной

математики

Протокол № от

Северодонецк 2011

УДК 519

Методические указания к самостоятельной работе по дисциплине “Дискретная математика” для студентов дневной и заочной форм обучения направления подготовки 6.050102 “Компьютерная инженерия ”.(электронное издание)/Сост. А.Е.Богданов -Северодонецк: ТИ ВНУ им. Владимира Даля, 2011. – 64 с.

Составлено на основании программы математических дисциплин для инженерно-технических специальностей высших учебных заведений.

Составитель: А.Е. Богданов, доц.

Ответственный за выпуск: О.В. Поркуян, доц.

Рецензент: А.Н. Иванов, доц.

Оглавление

1. Программа………………………………………………………….. 4

2. Индивидуальные задания…………………………………………. 6

3. Пример выполнения задания……………………………………… 43

Литература………………………………………………………........... 64

Программа

Раздел 1. Теория множеств.

1. Основные понятия теории множеств.

2. Соответствия. Функции. Отображения.

3. Понятие алгебры. Алгебра множеств Кантора.

4. Бинарные отношения.

5. Бинарное отношение эквивалентности.

6. Бинарное отношение порядка. Упорядоченные множества.

7. Решетки (структуры). Изоморфизм.

8. Отношения (обобщение). Алгебраические системы.

Раздел 2. Комбинаторный анализ.

1. Основные определения комбинаторного анализа.

2. Формулы расчета перестановок и сочетаний.

3. Бинома и полином

4. Подстановки

5. Метод включений и исключений

6. Метод производящих функций

Раздел 3. Теория графов.

1. Первоначальные понятия теории графов.

2. Операции над графами. Способы задания графов.

3. Маршруты, цепи, циклы и другие характеристики графа.

4. Алгебраическая форма представления графа (АФПГ).

Раздел 4. Некоторые приложения графов.

1. Эйлеровы графы. Алгоритм Флери. Гамильтоновы графы.

Метод Робертса-Флореса.

2. Пространство циклов графа.

3. Независимое (внутренне устойчивое) множество вершин

графа.

4. Вершинное число внешней устойчивости графа.

5. Плотность графа.

6. Раскраска графа.

7. Планарность графа.

Раздел 5. Оптимизационные алгоритмы теории графов.

1. Определение кратчайших путей. Алгоритм Дейкстры.

2. Максимальный поток через сеть. Алгоритм Форда-

Фалкерсона.

3. Алгоритм построения остова экстремального веса.

4. Задача коммивояжера: метод ветвей и границ. Ощая модель

задачи поиска.

5. Применение ориентированных деревьев в задачах теории

кодирования и диагностирования.

6. Алгоритм Гильберта-Мура построения оптимального дерева

бинарного поиска.

7. Сложность задач теории графов. Задача синтеза управляющих

систем.

Индивидуальные задания

1. Представить с помощью кругов Эйлера множественное выражение. Используя законы и свойства алгебры множеств, упростить заданное выражение.

2. Заданы множества кортежей. Показать, что эти множества представляют собой соответствия между множествами N₁ и N₂ , если N₁ = N₂ = . Дать полную характеристику этих соответствий.

3. Частично упорядоченное множество М задано множеством упорядо-ченных пар. Построить диаграмму и определить является ли данное множество решеткой. Если заданное множество является решеткой, то определить является ли решетка дедекиндовой , дистрибутивной.

4. Из колоды, содержащей 52 карты, вынули 10 карт. В скольких случаях среди этих карт окажется указанное количество указанных карт?

5. После обследования читательских вкусов оказалось, что 60% студентов читает журнал А, 65% − журнал В, 60% − журнал С, 55% − журнал Д, 40% − журналы А и В, 35% − журналы А и С, 30% − журналы А и Д, 40% − журналы В и С, 35% − журналы В и Д, 30% − журналы С и Д, 25% − журналы А, В и С, 20% − журналы А, В и Д, 20% − журналы А, С и Д, 15% − журналы В, С и Д, 10% − журналы А, В, С и Д. Сколько процентов студентов читает указанные журналы?

6. Решить рекуррентное соотношение.

7. Для неориентированного графа , у которого :

а) вычислить числа ;

б) определить хроматическое число .

8. Для заданной сети :

а) найти величину минимального пути и сам путь от вершины до вершины по алгоритму Дейкстры ;

б) используя алгоритм Форда-Фалкерсона, определить максималь-ный поток ( v₁ – вход , v₇ – выход сети ) и указать ми-нимальный разрез, отделяющий v₁ от v₇ ,

если задана матрица весов (длин, пропускных способностей) Р.

9. Используя алгоритм Краскала, построить остов с наименьшим весом для неориентированного взвешенного графа , у ко-торого , если заданы веса (длины) ребер.

ВАРИАНТ № 1

1.

2.

3. .

4. Хотя бы один «туз».

5. Не читает ни одного журнала.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 2

1.

2.

3. .

4. Ровно два «короля».

5. Читает только журнал А.

6.

7. .

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 3

1.

2.

3. .

4. Не менее трех «дам».

5. Читает только журналы А и В.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 4

1.

2.

3. .

4. Не более двух «валетов».

5. Читает только журналы А, В и С.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 5

1.

2.

3. .

4. Ни одного «короля».

5. Читает только один журнал.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 6

1.

2.

3. .

4. Хотя бы два «туза».

5. Читает менее четырех журналов.

6.

7. .

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 7

1.

2.

3. .

4. Ровно четыре «туза».

5. Читает не менее двух журналов.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 8

1.

2.

3. .

4. Не менее одного «валета».

5. Читает не более одного журнала.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 9

1.

2.

3. .

4. Не более трех «дам».

5. Читает только журнал В.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 10

1.

2.

3. .

4. Ни одного «туза».

5. Читает только журналы А и С.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 11

1.

2.

3. .

4. Хотя бы три «туза».

5. Читает только журналы А, В и Д.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 12

1.

2.

3. .

4. Ровно один «валет».

5. Читает только два журнала.

6.

7. .

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 13

1.

2.

3. .

4. Не менее двух «дам».

5. Читает менее трех журналов.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 14

1.

2.

3. .

4. Не более трех «королей».

5. Читает не менее трех журналов.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 15

1.

2.

3. .

4. Ни одного «валета».

5. Читает не более двух журналов.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 16

1.

2.

3. .

4. Хотя бы один «король».

5. Читает только журнал С.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 17

1.

2.

3. .

4. Ровно три «дамы».

5. Читает только журналы А и Д.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 18

1.

2.

3. .

4. Не менее двух «королей».

5. Читает только журналы А, С и Д.

6.

7. .

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 19

1.

2.

3. .

4. Не более двух «королей».

5. Читает только три журнала.

6.

7. .

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 20

1.

2.

3. .

4. Ни одной «дамы».

5. Читает менее двух журналов.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 21

1.

2.

3. .

4. Хотя бы два «короля».

5. Читает не менее одного журнала.

6.

7. .

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 22

1.

2.

3. .

4. Ровно два «валета».

5. Читает не более трех журналов.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 23

1.

2.

3. .

4. Не менее трех «валетов».

5. Читает только журнал Д.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

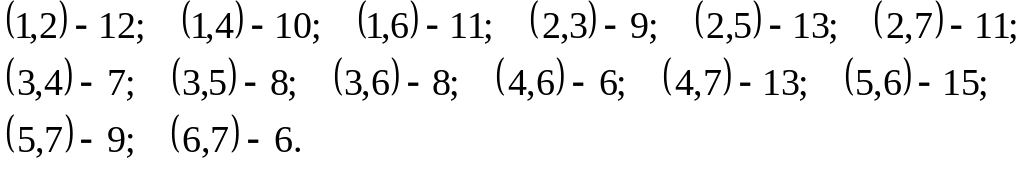
ВАРИАНТ № 24

1.

2.

3. .

4. Не более двух «дам».

5. Читает только журналы В и С.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 25

1.

2.

3. .

4. Хотя бы три «короля».

5. Читает только журналы В, С и Д.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 26

1.

2.

3. .

4. Ровно одна «дама».

5. Читает только журналы В и Д.

6.

7. .

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 27

1.

2.

3. .

4. Не менее трех «тузов».

5. Читает только один журнал.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 28

1.

2.

3. .

4. Не более двух «тузов».

5. Читает менее четырех журналов.

6.

7. .

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 29

1.

2.

3. .

4. Ровно две «дамы».

5. Читает не менее двух журналов.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 30

1.

2.

3. .

4. Не менее трех «королей».

5. Читает не более одного журнала.

6.

7. .

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 31

1.

2.

3. .

4. Ровно три «валета».

5. Читает только журналы С и Д.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 32

1.

2.

3. .

4. Не менее двух «тузов».

5. Читает не более трех журналов.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 33

1.

2.

3. .

4. Не более трех «тузов».

5. Читает только два журнала.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ВАРИАНТ № 34

1.

2.

3. .

4. Хотя бы две «дамы».

5. Читает менее трех журналов.

6.

7.

.

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

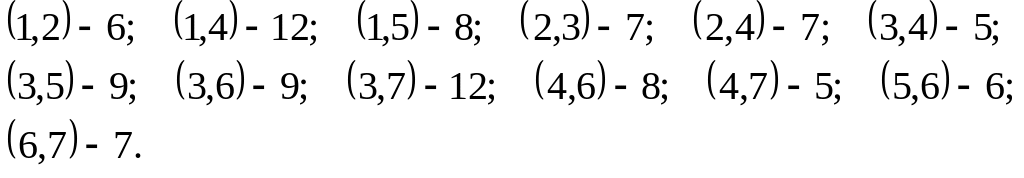
ВАРИАНТ № 35

1.

2.

3. .

4. Ровно три «короля».

5. Читает не менее трех журналов.

6.

7. .

v₁ v₂ v₃ v₄ v₅ v₆ v₇

8. Р = .

9.

ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ

1. Представить с помощью кругов Эйлера множественное выражение

.

Используя законы и свойства алгебры множеств, упростить заданное выражение.

□ Используя круги Эйлера и, учитывая, что операция пересечения вы-полняется раньше операции объединения, получим следующие рисунки:

Объединяя заштрихованные области, получим искомое множество:

Упростим заданное выражение:

=

.

■

2. Заданы множества кортежей:

.

Показать, что эти множества представляют собой соответствия между множествами N₁ и N₂ , если N₁ = N₂ = . Дать полную характеристику этих соответствий.

□ Найдем декартово произведение:

Видно, что заданные множества являются подмножествами этого пря-мого произведения. Следовательно, данные множества есть соответствия.

а) .

Область определения: . Следовательно, соответствие является частично определенным.

Область значений: . Следовательно, соответствие является сюръективным.

Образом элемента являются два элемента . Значит соответствие не является функциональным. Из этого следует, что соот-ветствие не является функцией, отображением.

б) .

Область определения: . Следовательно, соответствие является частично определенным.

Область значений: . Следовательно, соответствие не является сюръективным.

Образом любого элемента из является единственный элемент из . Следовательно, соответствие является функциональным, функци-ей. Соответствие является частично определенным. Это означает, что функция является частично определенной и не является отображением.

в) .

Область определения: .Следовательно,соответствие всюду определено.

Область значений: . Следовательно, соответствие не является сюръективным.

Образом любого элемента из является единственный элемент из . Следовательно, соответствие является функциональным, функци-ей. Так как соответствие всюду определено, то имеем полностью опреде-ленную функцию, т.е. имеем отображение N₁ в N₂ .

г) .

Область определения: . Значит, соответствие пол-ностью определено.

Область значений: . Значит, соответствие сюръек-тивно.

Образом любого элемента из N₁ является единственный элемент из N₂ . Следовательно, соответствие является функциональным, функцией.

Так как соответствие всюду определено, сюръективно, функционально и прообразом любого элемента из является единственный элемент из , то соответствие является взаимно однозначным.

Так как функция полностью определена и соответствие сюръективно, то имеем отображение N₁ на N₂ .

Так как для любых двух различных элементов из N₁ их образы из N₂ также различны, то отображение является инъективным.

Так как отображение является одновременно сюръективным и инъектив-ным, то имеем биективное отображение (взаимно однозначное отображе-ние).

■

3. Частично упорядоченное множество М задано множеством упорядо-ченных пар

.

Построить диаграмму и определить, является ли данное множество решеткой. Если заданное множество является решеткой, то определить, является ли решетка дедекиндовой , дистрибутивной.

□ Построим диаграмму:

Построим таблицу:

Пары элементов	Н.Г.	В.Г.	Н.Н.Г.	Н.В.Г.
1,2	1	2,5	1	2
1,3	1	3,4,5	1	3
1,4	1	4,5	1	4
1,5	1	5	1	5
1,6	1	6,2,5	1	6
2,3	1	5	1	5
2,4	1	5	1	5
2,5	2,6,1	5	2	5
2,6	6,1	2,5	6	2
3,4	3,1	4,5	3	4
3,5	3,1	5	3	5
3,6	1	5	1	5
4,5	4,3,1	5	4	5
4,6	1	5	1	5
5,6	6,1	5	6	5

Так как любая пара элементов имеет единственную наибольшую ниж-нюю грань и единственную наименьшую верхнюю грань, то заданное частично упорядоченное множество М является решеткой.

Решетка М является дедекиндовой, когда выполняется равенство:

для таких , что .

Решетка М не является дедекиндовой, т.к. указанное равенство не вы-полняется, например, для элементов 2, 3, 4:

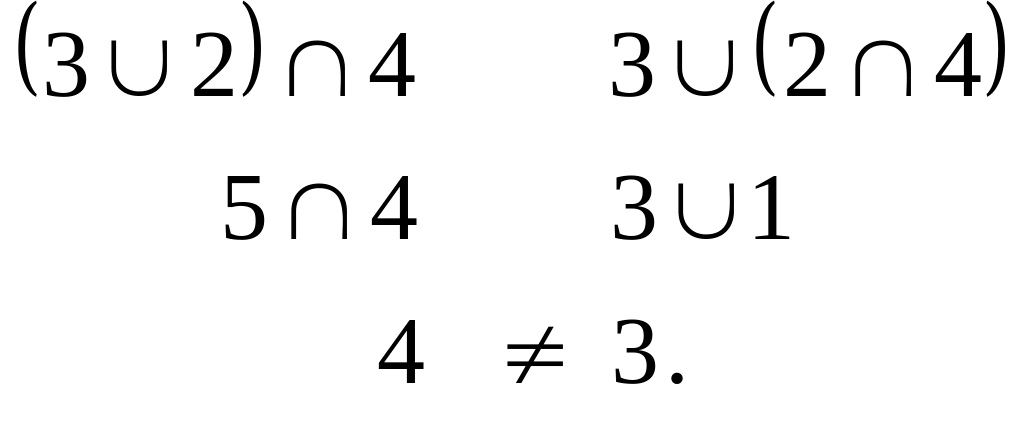
Одним из условий дистрибутивности решетки является ее дедекиндо-вость. Так как решетка М не является дедекиндовой, то она не является дистрибутивной решеткой.

■

4. Из колоды, содержащей 52 карты, вынули 10 карт. В скольких случаях среди этих карт окажется не более одной «шестерки»?

□ Не более одной «шестерки» означает, что среди извлеченных 10 карт может быть: либо ни одной «шестерки», либо одна «шестерка». Всего в колоде 4 «шестерки».

По правилу произведения:

− ровно нуль «шестерок» ( − нуль «шестерок» из четырех и − десять не «шестерок» из 48 карт, не содержащих «шестерок»);

− ровно одна «шестерка» ( − одна «шестерка» из четырех и − девять не «шестерок» из 48 карт, не содержащих «шестерок»).

Число не более одной «шестерки» среди выбранных 10 карт по правилу суммы будет равно

+ = =

=

=

= 47·46·44·43·41·39 + 16·47·46·22·43·41·5 = 6 540 715 896 + 6 708 426 560 =

= 13 249 142 456

■

5. При опросе сотрудников некоторого учреждения оказалось, что 60% сотрудников знают английский язык, 50% − французский, 50% − немецкий, 30% − английский и французский, 20% − французский и немецкий, 40% − английский и немецкий, 10% − английский, французский и немецкий. Сколько процентов сотрудников знают не менее двух языков.

□ Знать не менее двух языков – это знать два или три языка. Пусть − количество сотрудников, знающих не менее r языков из k языков. Тогда = + , где − количество сотрудников, знающих два языка; − количество сотрудников, знающих три языка. Количество сотрудников, знающих два языка, можно определить по формуле

,

т.е.

= + ,

где − количество сотрудников, знающих хотя бы два языка; − количество сотрудников, знающих три языка.

Пусть общее число сотрудников равно 1 или 100%. Тогда

= 0,3 + 0,2 + 0,4 = 0,9 и = 0,1 (по условию).

Следовательно,

1·0,9 − 3·0,1 = 0,6 или 60%.

По условию задачи = 0,1. Следовательно, количество сотрудников, знающих не менее 2 языков из 3 языков:

= 0,6 + 0,1 = 0,7 или 70%.

Для подсчета числа сотрудников, знающих не менее 2 языков, можно также воспользоваться формуле

= = = − =

= 1·0,9 − 2·0,1 = 0,2 или 70%.

■

6. Решить рекуррентное соотношение

□ Решить рекуррентное соотношение – это значит найти общий член последовательности , удовлетворяющей указанному рекуррентному соотношению.

Умножим заданное рекуррентное соотношение и просуммируем полученное выражение от нуля до бесконечности. В результате получим

или

,

или

.

Так как = , то

, , .

Тогда

) ) − ,

+ 9 t + 2t − 8t² = .

Отсюда

= = .

Методом неопределенных коэффициентов находим А, В и С:

,

пусть : , А = 1;

пусть : , В = −3;

пусть : , С = 2.

Тогда

= =

= = .

Следовательно, общий член последовательности имеет вид

= .

■

7. Для неориентированного графа , у которого ,

а) вычислить числа ;

б) определить хроматическое число .

□ Построим граф:

а) Вычислим числа .

1) :

Используя алгоритм выделения пустых подграфов, построим дерево:

Согласно определению :

.

2) :

Используя алгоритм выделения полных подграфов, построим дерево:

Здесь - полные подграфы. Видно, что мощность носителей всех под-графов равна трем, т.е.

.

3) :

Построим модифицированную матрицу смежности заданного графа G :

1 2 3 4 5 6

.

Находим минимальное число строк, покрывающих все столбцы модифи-цированной матрицы . Таких строк – одна. Следовательно,

.

б) Определим хроматическое число .

Согласно алгоритму минимальной раскраски вершин графа, выделим все пустые подграфы графа G , т.е. построим дерево (оно построено в пункте а) ):

Построим таблицу:

1 2 3 4 5 6

1. {1,4,6} 1 1 1

2. {1,5} 1 1

3. {2,5} 1 1

4. {2,6} 1 1

5. {3} 1

Определяем минимальное число строк, покрывающих все столбцы табли-цы. Такими строками могут быть строки 1, 3, 5. Значит,

.

Зададимся красками: для множества вершин - краска синяя (С ), для множества вершин - краска красная ( К ), для множества вер-шин - краска зеленая ( З ).

Раскрасим вершины графа G :

■

8. Для заданной сети :

а) найти величину минимального пути и сам путь от вершины до вершины по алгоритму Дейкстры ;

б) используя алгоритм Форда-Фалкерсона, определить максималь-ный поток ( v₁ – вход , v₆ – выход сети ) и указать ми-нимальный разрез, отделяющий v₁ от v₆ ,

если задана матрица весов (длин, пропускных способностей) Р :

v₁ v₂ v₃ v₄ v₅ v₆

□ Построим сеть:

а) Найдем величину минимального пути и сам путь сети G . Использу-ем для этого алгоритм Дейкстры.

Этап 1. Нахождение длины кратчайшего пути.

.

Шаг 1. Полагаем

1-я итерация.

Шаг 2. Составим множество вершин, непосредственно следующих за с временными метками: . Пересчитываем вре-менные метки этих вершин: ,

.

Шаг 3. Одна из временных меток превращается в постоянную:

Шаг 4. Следовательно, возвращаемся на второй шаг.

2-я итерация.

Шаг 2.

Шаг 3.

Шаг 4. Переход на второй шаг.

3-я итерация.

Шаг 2.

Шаг 3.

Шаг 4. Переход на второй шаг.

4-я итерация.

Шаг 2.

Шаг 3.

Шаг 4. Переход на второй шаг.

5-я итерация.

Шаг 2.

Шаг 3.

Шаг 4. Конец первого этапа.

Следовательно, длина кратчайшего пути равна .

Этап 2. Построение кратчайшего пути.

1-я итерация.

Шаг 5. Составим множество вершин, непосредственно предшеству-ющих с постоянными метками : Проверим равенство

для этих вершин:

т.е.

т.е.

Включаем дугу в кратчайший путь,

Шаг 6. Возвращаемся на пятый шаг.

2-я итерация.

Шаг 5.

Включаем дугу в кратчайший путь, .

Шаг 6. . Завершение второго этапа.

Следовательно, кратчайший путь построен. Его образует последователь- ность дуг: .

Окончательно, кратчайший путь от вершины до вершины v₆ пост-роен. Его длина (вес) равна . Сам путь образует последова-тельность дуг:

б) Определим максимальный поток через сеть G. Для этого используем алгоритм Форда-Фалкерсона.

Выбираем произвольно путь из вершины v₁ в вершину v₆ . Пусть это будет путь . Минимальную пропускную способ-ность на этом пути, равную 10, имеет дуга , т.е. Увеличим на этом пути поток до 10 единиц. Дуга становится насыщенной. Дуга имеет на данный момент пропускную спо-собность, равную 10.

Путь Следова-тельно, поток на этом пути можно увеличить на 9 единиц. Дуги становятся насыщенными.

Других маршрутов нет (другие маршруты проходят через насыщенные дуги). Поток максимален. Делаем разрез вокруг вершины v₁ по насы-щенным дугам

и получаем его величину единиц.

■

9. Используя алгоритм Краскала, построить остов с наименьшим весом для неориентированного взвешенного графа , у ко-торого , если заданы веса (длины) ребер:

□ Построим граф G :

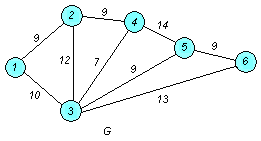
1. Упорядочим ребра в порядке неубывания веса (длины):

2. Возьмем ребро u₁ и поместим его в строящийся остов.

Возьмем ребро u₂ и поместим его в строящийся остов (т.к. оно не обра-зует с предыдущим ребром цикла).

Берем ребро u₃ и помещаеи его в строящийся остов (т.к. оно не образу-ет с предыдущими ребрами цикла).

Берем ребро u₄ и помещаем его в строящийся остов (т.к. оно не образу-ет с предыдущими ребрами цикла).

Берем ребро u₅ и помещаем его в строящийся остов (т.к. оно не образу-ет цикла с предыдущими ребрами).

Проверим окончание алгоритма. Число входящих в остов ребер равно 5. Заданный граф имеет п = 6 вершин и . Таким образом, остов содержит все вершины заданного графа G .

Вес (длина) построенного остова

равен .

■