Параграф 1.7. Физические основы анализа Фурье.

Рассмотрим систему которая обладает “N” степенями свободы, тогда одна из ненормальных координат системы будет представлять собой сумму гармонических колебаний различных частот , ,… .

Для простоты выберем начало отсчета таким образом, чтобы начальные фазы всех колебаний равнялись “0”, тогда результирующая колебаний будет:

Рассмотрим простейший случай когда интервалы между соседними частотами одинаковы.

Вычислим эту сумму

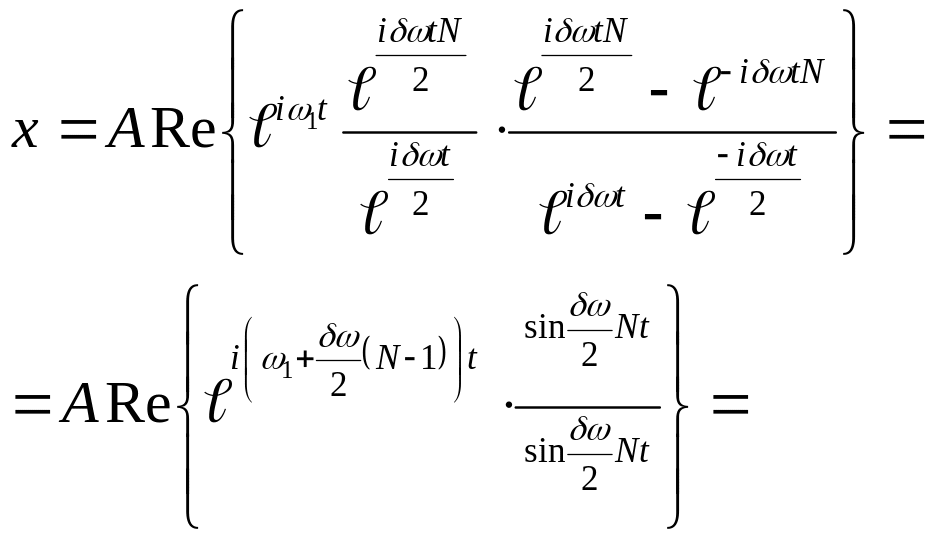
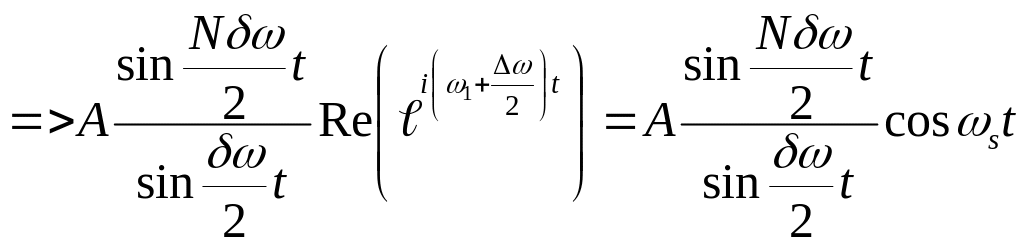
где - средняя частота.

Таким образом, при сложении большого числа колебаний с различными частотами, мы получили колебания с некоторой средней частотой , амплитуда которого 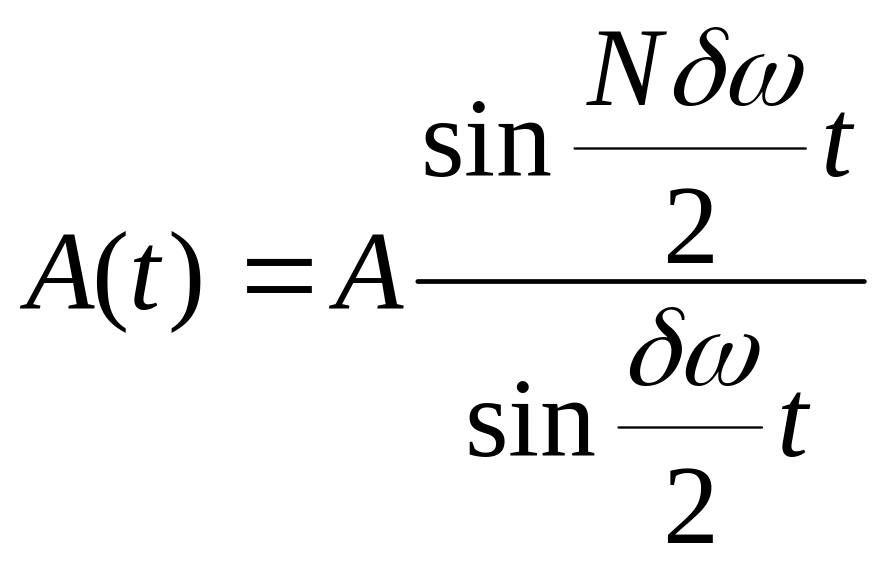зависит от времени.

В этой зависимости амплитуды особой точки есть особая точка где

Для вычисления амплитуды в этой точке воспользуемся правилом Лопиталя.

Рассмотрим случай когда N >> 1 т.е. тогда

А при малых углах

Таким образом, в результате сложения большого количества колебаний, мы получили ограниченное по времени колебание- импульс колебания. За длительность импульса колебания выбирают половину временного интервала между ближайшими максимумами нулей амплитуды.

Следует заметить, что справедливо и обратное утверждение: любой произвольный импульс колебания x(t) можно представить в виде суммы гармонических колебаний с различной амплитудой и частотой, такое представление называется анализом Фурье.

Зависимость амплитуды и складываемых колебаний A(t) называется спектром колебаний.

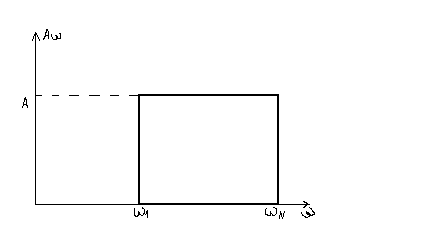
Интервал называется шириной спектра колебаний.

В рассмотренном примере мы получили соотношение между длительностью импульса и шириной спектра колебаний.

Т.к. был выбран частный случай, мы получили частное соотношение. В общем виде

Из этого неравенства следует, что чем короче импульс, тем шире у него спектр колебаний.

Затухающие колебания , тогда

Глава 2. Волны. Параграф 2.1 Волновой процесс. Волновая функция.

Решение этого уравнения будем искать в виде функции:

подставим эту функцию в наше уравнение:

и убеждаемся что она является решением.

Полученное решение f(x-vt) представляет собой возмущения, распространяющиеся со скоростью V вдоль оси OX.

То есть функция f(x) представляет собой волновую функцию. Общее решение уравнения будет

Рассмотрим трехмерный случай:

Рассмотрим сферически симметричное решение:

В этом случае волновое уравнение удобно переписать из координат x,y,z в переменную R

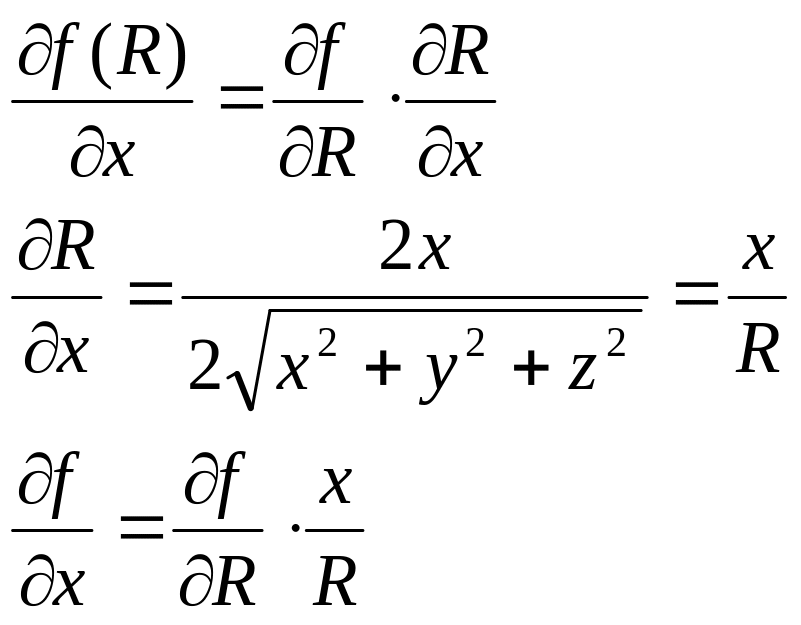
Т.е. мы получаем одномерное волновое уравнение.

Решение, которого, уже найдено.

представляет собой возмущение созданное в точке R=0 и уменьшающиеся по величине при распространении бесконечности

описывают возмущение которое возникает из ничего на бесконечности и растет при приближении к центру – такое решение физически невозможно.

§ 2.2. Гармонические волны.

Рассмотрим волновую функцию вида .

.

Циклическая частота или частота волны.

- фаза волны.

А – амплитуда волны. A=const.

F(R, t) называется гармонической или монохроматической волной.

Для того, чтобы рассматриваемая функция являлась решением волнового уравнения , должны удовлетворять некоторому уравнению, которое называется дисперсионным. .

Для того, чтобы получить уравнение, подставим гармоническую функцию в уравнение.

Решая это дисперсионное уравнение, мы можем найти частоту, как функцию k. . Полученное решение называется дисперсионным соотношением.

Точки в пространстве, фазы которых одинаковы. , образуют поверхность, которая называется волновой или волновым фронтом. Как известно, градиент любой функции направлен перпендикулярно поверхности, на которой она постоянна.

Т. к постоянен по величине и направлению, то волновая поверхность будет плоской. Поэтому данная гармоническая волна называется плоской гармонической волной. При этом направление распространения будет совпадать с направлением распространения . Расстояние, на котором фаза волны равна , называется длиной.

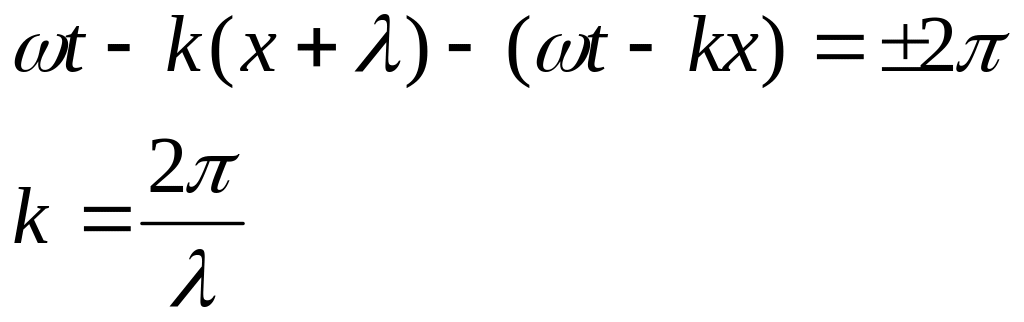
Время, в течение которого фаза волны меняется на , называется периодом волны. .

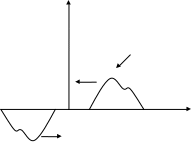
Пусть в такой среде распространяется волна. Из нулевого граничного условия следует, что

f

x

f

y

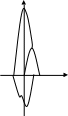
Таким образом, происходит изменение направления распространения на границе среды. Такое явление называется отражением.

Изменение звуковолновой функции в рассмотренном примере связано с исключительно с видом граничного условия.

Рассмотрим гармоническую волну, которая распространяется в граничной среде с нулевым граничным условием.

f

узел

x

Рассмотрим случай гармонического колебания в среде никакого распространения волны наблюдаться не будет.

Полученное возмущение называется стоячей волной.

Точки, в которых амплитуда колебаний равна нулю, называется узлами стоячей волны.

При переходе через узел фаза колебаний изменяется на .

Где n=1, 2, 3,…

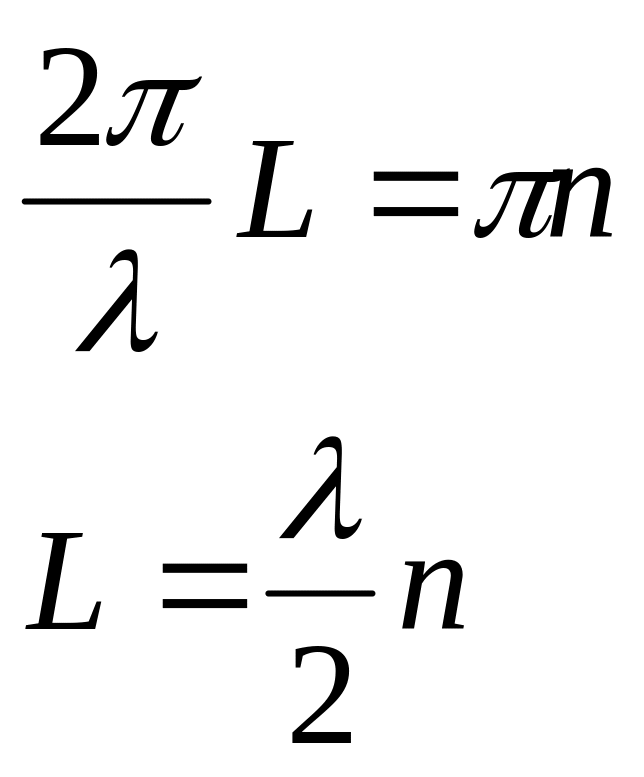
В полностью ограниченной среде возможны собственные моды лишь с определенной длиной волны (частотой).