
- •Дифференциальное исчисление функций одной переменной в упражнениях и задачах.
- •Глава 1. Введение в анализ
- •Определение функции
- •Предел функции
- •1.3. Непрерывность функций
- •Глава 2. Дифференциальное исчисление функции одной переменной
- •2. 1. Задачи, приводящие к понятию производной
- •2.2. Определение производной
- •2.3. Дифференцирование функций
- •2.4. Приложения производной к задачам геометрии и механики.
- •2.5. Производные высших порядков
- •Применение второй производной в задачах механики
- •Дифференциал функции
- •2.8.Основные теоремы о дифференцируемых функциях
- •2.9.Раскрытие неопределенностей. Правило Лопиталя
- •2.9. Исследование функций с помощью производных
- •2.10. Локальный экстремум функции
- •2.11.Наибольшее и наименьшее значения функции
- •2.12. Выпуклость кривой. Точки перегиба
- •2.13. Асимптоты графика функции
- •2.14. Общая схема исследования функции
- •2.15. Формула Тейлора
- •2.16.Векторная функция скалярного аргумента
- •2.17.Дифференциал длины дуги
- •2.18.Кривизна
- •Радиус, центр и круг кривизны. Эволюта и эвольвента
- •Литература
- •Содержание
- •Глава 1. Введение в анализ………………………………………3
- •1.1. Определение функции………………………………………………….3
- •Глава 2. Дифференциальное исчисление функции одной переменной………………………………………………………..28
2.15. Формула Тейлора
Если
функция
![]() непрерывна и имеет на отрезке
непрерывна и имеет на отрезке
![]() непрерывные производные до
непрерывные производные до
![]() го
порядка включительно, а в каждой
внутренней точке отрезка имеет конечную
производную п
– го
порядка, то при
го
порядка включительно, а в каждой
внутренней точке отрезка имеет конечную
производную п
– го
порядка, то при
![]() справедлива следующая формула Тейлора:
справедлива следующая формула Тейлора:
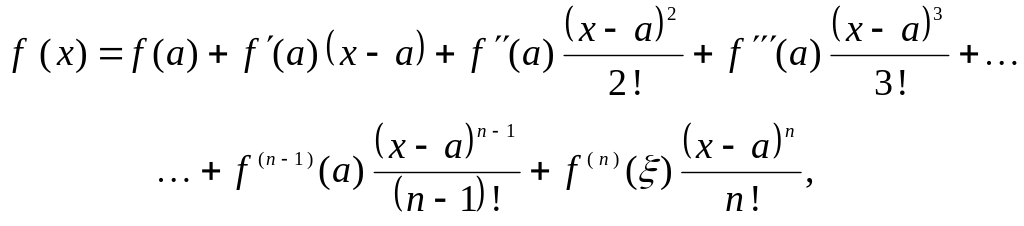
где
![]()
![]()
![]() -
остаточный член формулы Тейлора в форме
Лагранжа :
-
остаточный член формулы Тейлора в форме
Лагранжа :
![]() ,
,
Формула Тейлора позволяет приближенно представить (аппроксимировать) произвольную функцию в вид многочлена
![]()
Если
в формуле Тейлора положить
![]() ,
то она записывается в виде
,
то она записывается в виде
![]()
где
![]()
Полученный частный случай формулы Тейлора называется формулой Маклорена.
Остаточный член в формуле Маклорена имеет вид
![]()
Пример.
Разложить многочлен
![]() по степеням двучлена
по степеням двучлена
![]() ,
пользуясь формулой Тейлора.
,
пользуясь формулой Тейлора.
Решение.
Найдем значения многочлена и его
производных в точке
![]() :
:
![]()
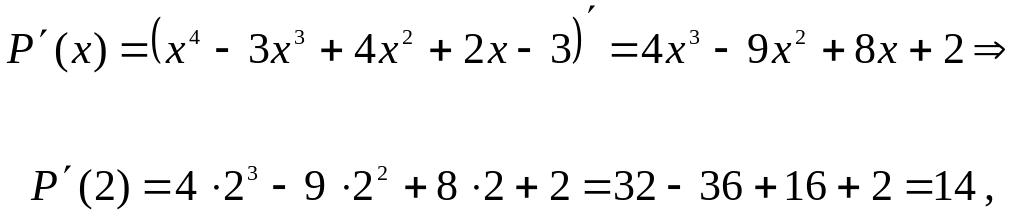

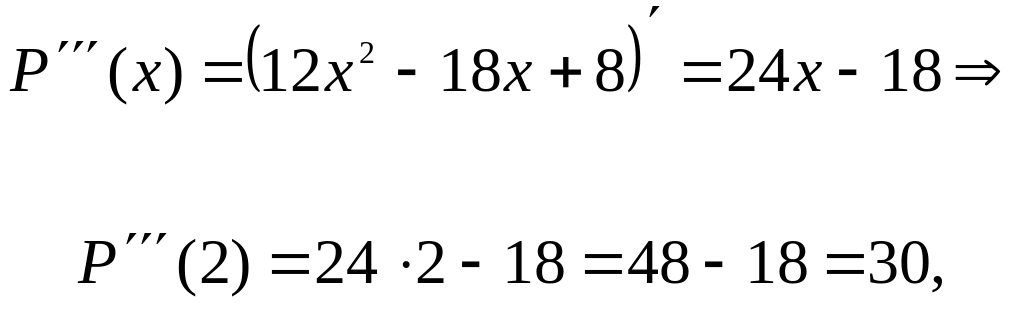
![]() ,
,
![]() при
любом х.
при
любом х.
Подставляя найденные значения в формулу Тейлора
![]() ,
,
получим

Следовательно,
![]()
Пример.
С помощью формулы Маклорена разложить
функцию
![]() .
.
Решение. Вычислим значение функции в точке х = 0:
![]()
Найдем производные функции первого, второго, …,
п – го порядков и их значения в точке х = 0:
![]()
![]()
![]()
![]()
![]()
продолжая по аналогии, получим
![]()
Подставляя найденные значения в формулу Маклорена
![]()
получим

Следовательно, разложение функции в точке х = 0 имеет вид
![]()
Пример.
Сколько
нужно взять членов в формуле Маклорена
для функции
![]() ,
чтобы получить многочлен, представляющий
эту функцию на отрезке
,
чтобы получить многочлен, представляющий
эту функцию на отрезке
![]() ,
с точностью до 0, 001?
,
с точностью до 0, 001?
Решение. Так как производные для функции любого порядка
![]() ,
,
то их значения при х = 0
![]() ,
,
![]()
Отсюда
![]()
где
![]()
Так
как, по условию
![]() и
и
![]() ,
то
,
то
![]()
Следовательно, если выполняется неравенство
![]()
то будет выполняться неравенство
![]()
и
для этого достаточно взять
![]() .
.
Таким образом, в формуле Маклорена достаточно взять семь членов.
Упражнения.
1.
Разложить
многочлен
![]() по степеням двучлена
по степеням двучлена
![]() ,
пользуясь формулой Тейлора.
,
пользуясь формулой Тейлора.
2. С помощью формулы Маклорена разложить по степеням х функцию
а)
![]() ,
б)
,
б)
![]()
3. При каких значениях х приближенная формула
![]() имеет
погрешность меньше 0, 00005 ?
имеет
погрешность меньше 0, 00005 ?
2.16.Векторная функция скалярного аргумента
Из
курса линейной алгебры известно, что
разложение любого вектора
![]() ,
проекции которого на оси координат
равны х,
у
и
z,
имеет вид
,
проекции которого на оси координат
равны х,
у
и
z,
имеет вид
![]() ,
,
где![]() и
и
![]() —
единичные векторы, направленные по осям
координат. Если проекции х,
у,
z
—
постоянные числа, то вектор
называется постоянным.
Если
проекции вектора
являются функциями: параметра
t,
изменяющегося
в некотором интервале:
—
единичные векторы, направленные по осям
координат. Если проекции х,
у,
z
—
постоянные числа, то вектор
называется постоянным.
Если
проекции вектора
являются функциями: параметра
t,
изменяющегося
в некотором интервале:
x = x (t), y = y (t), z = z (t),
тогда
вектор
![]() называется переменным;
при
этом каждому значению параметра t
будет
соответствовать определенный вектор:
называется переменным;
при
этом каждому значению параметра t
будет
соответствовать определенный вектор:
![]() .
.
Определение. Если каждому значению параметра t соответствует определенный вектор , то он называется вектор – функцией скалярного аргумента.
Вектор есть радиус – вектор r некоторой точки на заданной линии, то эту линию можно задать векторным уравнением:
![]() .
.
Определение.
Пространственная
кривая, описанная концом вектора
,
называется
годографом вектор - функции
![]() =
=
Начало координат называют при этом полюсом годографа.
Определение.
Вектор
называется
пределом вектор – функции
при
![]() :
:
![]() .
.
Определение. Вектор-функция называется непрерывной при данном значении пapаметра t, если она определена в окрестности точки t и если
![]() .
.
Определение. Предел
![]()
называется производной от векторной функции пo скалярному аргументу t и обозначается
![]()
Производная вектор – функции может быть вычислена по формуле
![]()
Производная
![]() есть вектор, направленный по касательной
к годографу вектора
в
сторону возрастания параметра
t
.
есть вектор, направленный по касательной
к годографу вектора
в
сторону возрастания параметра
t
.
Основные правила дифференцирования переносятся без изменения на вектор – функцию.
Уравнение касательной к пространственной кривой в точке М0 (х0, у0, z0 ) имеет вид
![]() ,
,
уравнение нормальной плоскости имеет вид
![]()
где
![]()
Дифференциал дуги пространственной кривой вычисляется по формуле
![]()
Пример.
Найти производную вектор – функции
![]() .
.
Решение. Найдем производные
![]()
Подставим найденные выражения в формулу
![]()
и получим
![]()
Следовательно,
производная вектор – функции
![]()
![]()
Пример.
Найти производную вектор – функции
![]() в точке
в точке
![]() .
.
Решение. Найдем производные и вычислим их значения при :
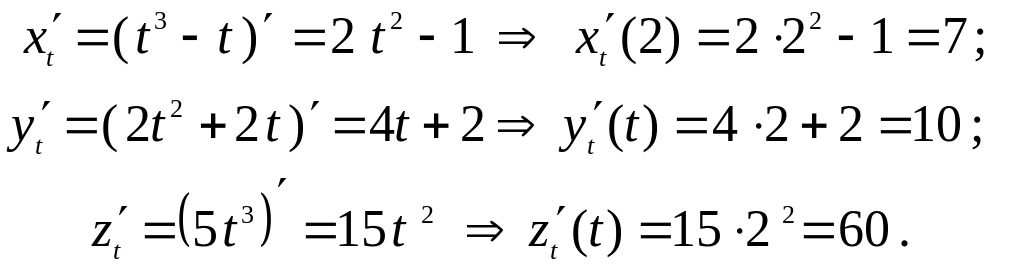
Подставляя значения производных в формулу
получим
![]()
Следовательно, производная вектор – функции в точке
![]()
Пример.
Найти уравнения касательной прямой и
нормальной плоскости к кривой
![]() при
при
![]()
Решение. Определим координаты точки касания:
![]()
Найдем производные от х, у, z по t и вычислим их значения в точке касания :

Подставляя
найденные значения
![]()
![]()
![]()
![]() в
уравнение касательной прямой к
пространственной кривой
в
уравнение касательной прямой к
пространственной кривой
![]()
и уравнение нормальной плоскости
![]()
Получим
![]()
![]()
Следовательно,
уравнение касательной к пространственной
кривой –![]() –
–
![]()
уравнение нормальной плоскости –
![]()
Пример.
Найти дифференциал дуги кривой
![]()
Решение. Найдем производные от х, у, z по t :
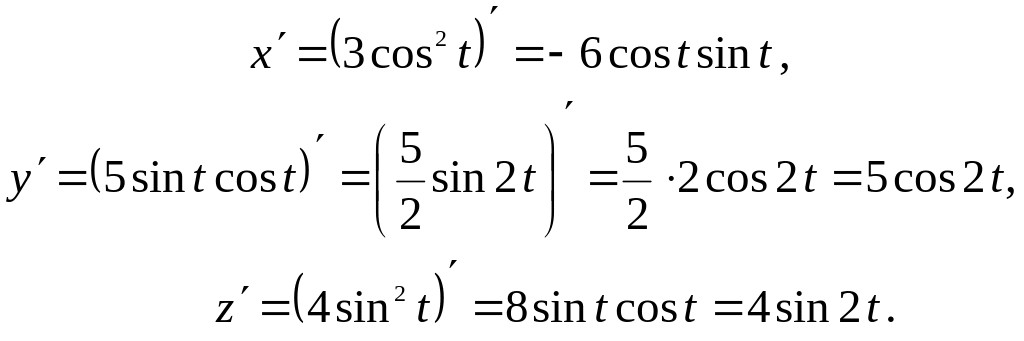
Подставляя найденные значения
![]()
в формулу
![]()
получим

Следовательно,
дифференциал дуги кривой
![]()
![]()
![]()
![]()
Упражнения
1. Найти производную вектор – функции:
а)
![]() ;
;
б)
![]() в точке
в точке
![]() .
.
2. Найти уравнения касательной прямой и нормальной плоскости к кривой:
а)
![]() при
при
![]() ;
;
б)
![]() ,
при
,
при
![]() .
.
3. Найти дифференциал дуги кривой :
а)
![]()
б)
![]() .
.
