1. Методы отделения корней уравнения.

Отделение корней можно осуществить аналитическим и графическим способами:

I. Чтобы отделить корень аналитически, достаточно найти такой отрезок [a, b], на котором выполняются 3 условия:

1) f (a)*f(b) <0

2) f (x) – непрерывная на [a , b] функция

3) f (x) – монотонная на [a , b] функция.

II. Чтобы отделить корень графически, необходимо построить график функции f(x) на промежутке изменения x, тогда абсцисса точки пересечения графика функции с осью ОХ есть корень уравнения.

Уравнение можно заменить равносильным f(x)= . Строят графики этих функций, тогда искомый корень является абсциссой точки пересечения этих графиков.

2. Уточнение корней уравнения. Метод деления отрезка пополам, метод секущих.

Уточнить корень – значит найти его приближенное значение с заданной погрешностью e.

Самый простой метод, пригодный для любых непрерывных функций – метод деления отрезка пополам. Это самый простой метод вычисления корня уравнения. Разделим исходный отрезок [a,b] пополам c=(a+b)/2 .

Проверяя знаки f(a), f(b), f(c) выясним в каком из отрезков [a,c] или [c,b] содержится корень

x* є [a,c] , если f(a)f(c)<0 ;

x* є [c,b] , если f(c)f(b)<0 .

Выбранный отрезок принимаем за [a,b] и повторяем это до тех пор пока получаемый отрезок не сожмется до заданной степени точности. При n итерациях получим соотношение (b-a)/2n <= e, из которого можно вычислить число итераций, необходимое для достижения заданной степени точности n>= ln2(b-a)/e .

Ввиду медленной сходимости этот метод редко используется для нахождения значения корня, обычно его применяют для локализации корня с дальнейшим уточнением значения корня каким-либо другим методом.

Метод секущих. Этот метод можно получить из метода Ньютона заменив производную f'(x) отношением разности функции к разности аргумента в окрестности рассматриваемой точки

f '(x) ~( f(x+h) - f(x))/h.

Подставляя это выражение в x_k+1 = x_k - f(x_k)/f '(x_k) получим

x_i+1 = x_i - f(x_i)h / (f(x_i+h)-f(x_i)) (1)

Геометрически это означает, что приближенным значением корня считается точка пересечения секущей, проходящей через две точки функции f(x_i) и f(x_i+h), с осью абсцисс.

П ри использовании этого метода следует уменьшать величину h по мере приближения к корню.

Вариацией этого метода является метод ложных положений. В нем для проведения секущей используются текущая и предыдущая точки. Первое приближение вычисляется по формуле (1), а остальные по формуле x_i+1 = x_i - f(x_i)(x_i-1 - x_i) /(f(x_i-1) -f(x_i)).

3. Уточнение корней уравнения. Методы касательных (Ньютона).

f(x)=0. Предположим, что f(x) имеет корень с на отрезке [a,b] и дифференцируема на этом отрезке, причём f’(x) не обращается в нуль.

Возьмём произвольную точку x₀ [a,b] и запишем в этой точке уравнение касательной y=f(x₀)+f’(x₀)(x-x₀).

Графики функций f(x) и её касательной близки около точки касания, поэтому естественно ожидать, что точка x₁ пересечения касательной с осью ОХ будет находиться недалеко от корня с. Для определения точки x₁ имеем уравнение:

f(x₀)+f’(x₀)(x₁-x₀)=0

Повторим проделанную процедуру: написав уравнение касательной графика функции f(x) при x=x₁ и найдя точку пересечения x₂ с осью ОХ, получим

Продолжая этот процесс, получаем:

Достаточные условия сходимости метода касательных: пусть f(x) определена и дважды дифференцируема на отрезке [a,b], причем f(a)*f(b)<0, и производные f’(x) и f’’(x) сохрняют постоянный знак на отрезке [a,b], тогда исходя из начального приближения x₀ [a,b], удовлетворяющего неравенству f(x₀)*f’’(x₀)>0, можно построить последовательность , сходящуюся к единственному на [a,b] решению уравнения f(x)=0.

Геометрическая интерпретация такова: если через точку с координатами (x_n,f(x_n)) провести касательную, то абсцисса точки пересечения касательной с осью ОХ есть очередное приближение x_n+1 к корню уравнения.

Итерационный процесс можно прекращать, если .

4. Аппроксимация функций.

Задача заменить функцию f(x_i), заданную таблицей, непрерывной функцией Q(x), необязательно совпадающей с f(x_i) во всех точках, но достаточно близкой к ней. Такая задача называется задачей приближения или аппроксимацией функции.

Функция f(x_i) называется аппроксимируемой.

Функция Q(x) называется аппроксимирующей.

Классической теорией приближения Q(x) выбирают в классе степенных многочленов.

Таким образом,будем рассматривать аппроксимацию функции y_i=f(x_i),i=0,n полиномом степени m.

Q_m(x)=a₀+a₁x+…+a_nx_m, m n.

Для решения задачи аппроксимации необходимо выбрать меру близости полинома к заданным точкам.

5. Квадратичная аппроксимация (МНК).

МНК заключается в том, чтобы построить такой полином Q_m(x)= , что сумма квадратичных отклонений значений аппроксимируемой и аппроксимирующей функций, называемая квадратичным отклонением, в узлах была бы минимальной.

Очевидно, что минимума квадратичного отклонения Φ можно добиться засчёт изменения коэффициентного полинома Q_m(x) a₀, a_m. Условием минимума является равенство 0 частных производных по всем коэффициентам a₀,…,a_m. Это дает систему m+1 уравнения с m+1 неизвестным.

…

Раскрывая скобки и выполняя суммирования получаем:

+ +…+a_m

Система представляет собой СЛАУ относительно коэффициента а_i . Решив систему, построим полином Q_m(x), аппроксимирующий функцию y_i=f(x_i) и минимизирующий квадратичное отклонение.

Можно доказать, что если среди точек х₁, х₂,…, x_n нет совпадающих, m≤n, то определитель системы отличен от нуля, следовательно, система имеет единственное решение.

Замечание: Функция Q(x) необязательно должна быть представлена полиномом вида . Единственным критерием выбора этой функции является возможность минимизации суммы квадратов отклонений. Как правило, используют аппроксимирующий полином не выше 3-ей степени.

{ - разность между аппроксимируемой и аппроксимирующей функциями.

Мы минимизируем сумму площадей квадратов, построенных на разности.

6. Интерполяция функций. Интерполяционный полином Лагранжа.

Пусть задано несовпадающее множество точек x_i, которое мы будем называть узлами и в которых известны значения f(x_i), i=0,n.

1. Способ построения аппроксимирующей функции, при котором в узлах значения аппроксимирующей и аппроксимируемой функции совпадают, называется интерполяцией.

2. Интерполяция – это частный случай аппроксимации, когда аппроксимирующая прямая проходит через точки таблицы.

Если аппроксимирующую функцию строить только по некоторым точкам таблицы, то эти точки называются узлами интерполяции и аппроксимирующая прямая проходит через узлы интерполяции.

В качестве аппроксимирующей функции возьмём полином , тогда задача интерполяции заключается в том, чтобы найти такой полином Q_m(x), который в заданных точках x_i принимает те же значения, что и f(x), т.е. Q_m(x_i)=f(x_i), то Q_m(x) называется интерполяционным полиномом.

Пусть m=n, тогда коэффициенты a_i можно определить из системы уравнений:

Определитель той системы – есть определитель Вандермонда:

Система имеет единственное решение, т.к. ∆≠0.

Полином Q(x)=Ln(x), коэффициенты которого определяются из этой системы, называется интерполяционным полиномом Лагранжа и может быть записан в виде:

m=n, где m – степень полинома, n – число узлов+1. Следовательно, степень полинома должна быть на 1 меньше числа узлов.

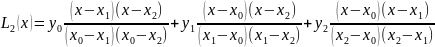
7. Численное дифференцирование.

Численное дифференцирование используется для приближенного вычисления производных функции заданной таблицей и для функций, которые по разным причинам неудобно или невозможно дифференцировать аналитически. В последнем случае вычисляется таблица функции в окрестности исследуемой точки и по этим значениям вычисляется приближенное значение производной.

Итак, пусть в точках x_i, i=0,1,2,...n известны значения функции y_i=f(x_i). Способ построения формул численного дифференцирования состоит в том, что по табличным точкам строится интерполянт P_n(x), который дифференцируется нужное число раз, и делается допущение о том, что производная от функции приблизительно равна производной от интерполянта

Погрешность такой формулы характеризуется k-той производной от ошибки интерполяции .

8. Численное интегрирование. Геометрический смысл численного интегрирования.

Задача численного интегрирования состоит в нахождении приближенного значения определенного интеграла от функции, заданной в виде таблицы.

Метод прямоугольников

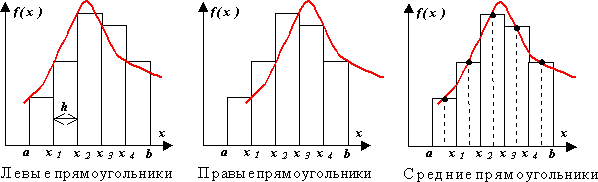
Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс.

М етод трапеции

Аппроксимация в этом методе осуществляется полиномом первой степени.

Метод Симпсона

Подынтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) – параболой, проходящей через три узла, например, как показано на рисунке ((1) – функция, (2) – полином).

9. Простейшие формулы численного интегрирования.

Квадратурная формула левых прямоугольников

Очевидно, что ее алгебраическая степень точности d=0 и формула является интерполяционной.

Квадратурная формула правых прямоугольников

Квадратурная формула средних прямоугольников

Алгебраическая степень точности d=1 и формула является интерполяционной.

Квадратурная формула трапеций

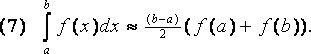
Квадратурная формула Симпсона

10. Обобщение простейших формул численного интегрирования.

?

11. Задача Коши для обыкновенного дифференциального уравнения 1-го порядка.

Задача Коши для обыкновенного дифференциального уравнения состоит в том, чтобы найти решение уравнения y' = f(x, y) (2) , удовлетворяющее начальным условиям

y(x₀) = y_0. (3)

Решение задачи Коши называется частным решением уравнения (2) при условии(3). Частному решению соответствует одна из интегральных кривых, проходящих через точку (x₀,y₀).

Будем искать приближенное решение этой задачи на конечном множестве точек отрезка [a, b], называемом сеткой:

x_i = x₀ + ih, x₀ = a, x_n = b,

h = (b-a)/n, i = 0,1,2,...,n.

Приближенным решением задачи будет некоторая сеточная функция y = y (x).

Для получения значений сеточной функции используются различные методы основанные на замене производной каким-либо разностным уравнением.

12. Метод Эйлера решения задачи Коши для ОДУ 1-го порядка.

Простейшим численным методом решения задачи Коши является метод ломанных Эйлера. Суть метода Эйлера заключается в замене функции y(x) на отрезке интегрирования прямой линией, касательной к графику в точке x=x_i. Если искомая функция сильно отличается от линейной на отрезке интегрирования, то погрешность вычисления будет значительной. Ошибка метода Эйлера прямо пропорциональна шагу интегрирования:

13. Одномерные задачи оптимизации.

Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. Если рассматривать функцию, то поиск наибольшего или наименьшего значения. Общие методы оптимизации:

1. аналитические методы, использующие классические методы дифференциального и вариационного вычисления

2. численные методы

3. графические методы

Функция f(x), заданная на a≤x≤b называется унимодальной на отрезке [a,b], если существует единственная точка x^* минимума f(x), т.е. f(x^*)= и если для любых двух точек x₁, x₂ [a,b] выполняются условия: f(x₁)>f(x₂), что следует из неравенства x₁<x₂≤x^* и f(x₁)<f(x₂), что следует из неравенств x₂>x₁≥x^*.

Метод дихотомии

Пусть задана унимодальная функция f(x). Необходимо найти минимум функции на отрезке [a,b], которому принадлежит точка локального минимума x^*. Для сужения отрезка унимодальности используем точки x₁, x₂, расположенные симметрично относительно середины отрезка [a,b].

Пусть известен отрезок [a_n-1;b_n-1], находим середину отрезка:

Вычисляем значения функции в точках x_n±δ, сравниваем их:

1) если f(x_n-δ)<f(x_n+δ), то a_n=a_n-1, b_n=x_n+δ

2) если f(x_n-δ)>f(x_n+δ), то a_n= x_n-δ, b_n=b_n-1

В результате приходим к последовательности вложенных отрезков, таких что точка локального минимума принадлежит каждому из них и является общим пределом последовательности.

Метод золотого сечения

Золотое сечение, открытое Евклидом, состоит в разбиении интервала [a,b] на 2 части точкой x₁ таким образом, чтобы отношение длины всего отрезка к большей части было равно отношению большей части к меньшей.

Коэффициент дробления отрезка [ a , b ] :

x₁=b+(1-k)(b-a)

x₂=b+k(b-a)

a x₁ x₂ b

Алгоритм:

1) вычисляем значения x₁, x₂

2) вычисляем значения f(x₁), f(x₂)

3) проверяем условия:

- если f(x₁)≤ f(x₂), то для дальнейшего деления оставляют интервал [a,x₂]

- если f(x₁)> f(x₂), то для дальнейшего деления оставляют интервал [x₁,b]

Процесс деления продолжают до тех пор, пока длина интервала неопределенности не станет меньше заданной точности ε.Замечание: x₁ производит золотое сечение интервала [a,x₂], x₂ – золотое сечение отрезка [x₁,b].

14. Многомерные задачи оптимизации.

Пусть f(x₁, x₂,…, x_n) – целевая функция. Задача поиска максимума этой функции сводится к минимизации функции - f(x₁, x₂,…, x_n), поэтому будем рассматривать задачу поиска минимума. Наибольшие трудности поиска минимума f(x) возникают, когда размерность n вектора x велика, поэтому важнейшей проблемой является уменьшение размерности вектора целевой функции на этапе построения математической модели. В модели следует сохранить только те x_i, которые сильнее других влияют на изменение целевой функции.

Линиями уровня f(x₁, x₂) называют семейство линий плоскости R², на которых функция принимает постоянное значение.

Неявным уравнением линии уровня является уравнение вида f(x₁, x₂)=с.

Если функция f(x) имеет единственную точку минимума x^*(x₁^*, x₂^*), то функция называется мономодальной и линии уровня имеют следующий вид: