
Лабораторная работа № 8
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРИЧЕСКИХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Цель работы: изучение электрических затухающих колебаний в колебательном контуре, измерение периода, логарифмического декремента затухания, коэффициента затухания, добротности и индуктивности контура.
Приборы и принадлежности: генератор звуковой частоты, осциллограф, катушка, конденсаторы и резисторы на модуле МОЗ. Набор стержней -сердечников катушки.
Введение
Замкнутая электрическая цепь, состоящая из конденсатора С, соединенного последовательно с катушкой индуктивности L, называется колебательным контуром. Реальный колебательный контур обладает электрическим сопротивлением, которое на схеме обозначено в виде резистора R.
Рассмотрим электрическую цепь, состоящую из колебательного контура
С, L, R и источника постоянного тока, ЭДС которого (рис. 1).
Рис.
1.
![]() ,
(1)
,
(1)
где i - ток в цепи, и - напряжение на конденсаторе, с - ЭДС самоиндукции катушки.
Подставим в
уравнение
(1) ЭДС
самоиндукции
![]()
-2-
![]() .
(2)
.
(2)
В этом выражении несколько неизвестных переменных величин: i, u, di/dt. Выразим их через одну переменную, например, через напряжение на конденсаторе и, учитывая, что
![]() ,
,
![]() ,
,
![]() .
.
Тогда уравнение (2) примет вид
![]() ,
(3)
,
(3)
или
![]() .
(4)
.
(4)
Заменим
![]() ,
,
![]() ,
и перепишем уравнение
(4)
,
и перепишем уравнение
(4)
![]() ,
(5)
,
(5)
где - коэффициент затухания, о - циклическая частота незатухающих колебаний в колебательном контуре.
Уравнение (5) является дифференциальным уравнением второго порядка, решая которое можно получить зависимость напряжения на конденсаторе и от времени t.
Сначала рассмотрим случай, когда сопротивление контура R = 0. Уравнение (5) в этом случае будет выглядеть так:
![]() .
(6)
.
(6)
Его решением будет гармоническая функция
![]() .
(7)
.
(7)
При t = 0 (момент переключения переключателя П из положения 1 в положение 2, рис. 1 ) напряжение на конденсаторе максимально и = Um и ток в контуре равен нулю, i = 0. При этих начальных условиях начальная фаза = 0 и уравнение (7) приобретает вид
![]() ..
(8)
..
(8)
Здесь 0- собственная частота колебательного контура, которая определяется его параметрами L и С
![]() .
(9)
.
(9)
-3-
Следует отметить, что наряду с колебаниями напряжения и на конденсаторе будут изменяться с той же частотой в контуре и другие физические величины: заряд на пластинах и напряженность электрического поля в конденсаторе, ток в контуре и магнитная индукция в катушке.
Если активное сопротивление контура R не велико, так что 2 << 20, то уравнение (5) имеет следующее решение:
![]() ,
(10)
,
(10)
где Umo - напряжение на конденсаторе в начальный момент времени t = 0. В этот момент и = Umo, следовательно, начальная фаза колебаний = 0.
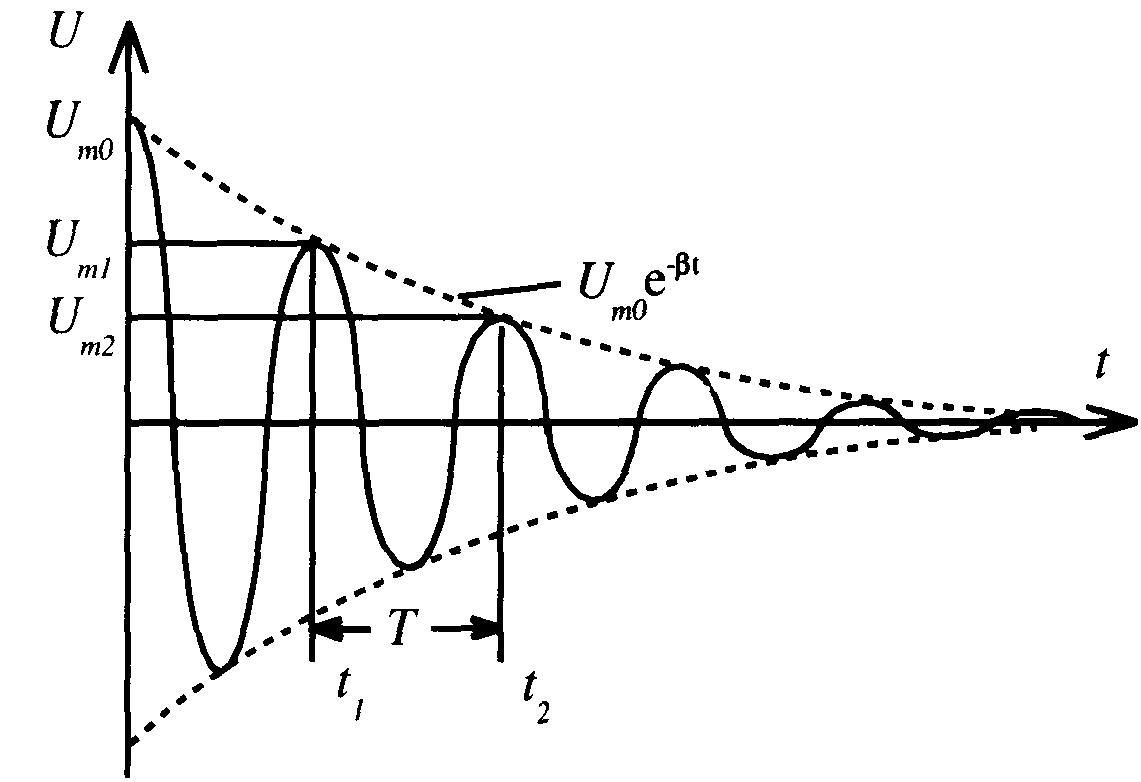
Частота затухающих колебаний зависит от параметров колебательного контура L и С, так как о зависит от них, а также от коэффициента затухания
![]() .
(11)
.
(11)
За период колебаний в этом случае можно принять величину
![]()
Рис.2
![]() .
(12)
.
(12)
Логарифмический декремент затухания связан с коэффициентом затухания и периодом колебаний Т следующим образом:
![]() .
(13)
.
(13)
При слабом затухании
0
период можно считать равным
![]() ,
,
![]() ;
;
![]() .
(14)
.
(14)
Для характеристики колебательных свойств системы применяется величина Q, называемая добротностью контура, которая также связана с длительностью процесса затухания колебаний. Она определяется так:
-4-
![]() .
(15)
.
(15)
Добротность обладает простым физическим смыслом. Амплитуда напряжения на конденсаторе убывает со временем по закону е-T. Энергия заряженного конденсатора пропорциональна квадрату амплитуды напряжения, т. е. энергия уменьшается как е-2T. Относительное уменьшение энергии за один период колебаний будет таким:
![]() .
.
При небольшом затухании логарифмический декремент затухания < 1,
поэтому
![]() ,
откуда
,
откуда
![]()
Подставив это выражение в формулу (15), получим
![]() (16)
(16)
Таким образом, добротность колебательного контура Q пропорциональна отношению энергии, содержащейся в контуре, к потерям энергии W за время одного колебания (за период).
Рассмотрим случай сильного затухания, когда = 0 . Согласно формуле (11) колебания в таких условиях становятся невозможными, так как = 0, напряжение на конденсаторе уменьшается со временем апериодически
![]() .
(17)
.
(17)
Такой процесс имеет место в том случае, если активное сопротивление контура достигает критической величины (или превышает ее). Значение критического сопротивления можно найти из условия 2 = 2 .
![]() ,
,
![]() .
(18)
.
(18)
Следует иметь в виду, что величина критического сопротивления определяется не только активным сопротивлением контура, но и другими потерями в контуре - рассеянием электромагнитного поля, потерями в диэлектрика конденсатора, потерями на перемагничивание магнетика и токами Фуко если магнитное поле катушки пронизывает соответствующие предметы, находящиеся внутри или вблизи колебательного контура.
