60

ВЫСШАЯ МАТЕМАТИКА

Учебный комплекс для студентов – экономистов 1-го курса

Второй семестр

1. Интегрирование

Неопределенный интеграл

Основной операцией дифференциального исчисления является дифференцирование - нахождение производной данной функции. Обратной к этой операции является интегрирование – отыскание функции по известной ее производной. В этом разделе рассматриваются некоторые из основных методов и приемов интегрирования.

Функция , для которой выполняется равенство для всех из области определения , называется первообразной функции . Несколько примеров первообразных для различных функций приведем в следующей таблице.

Таблица 1.

0
1

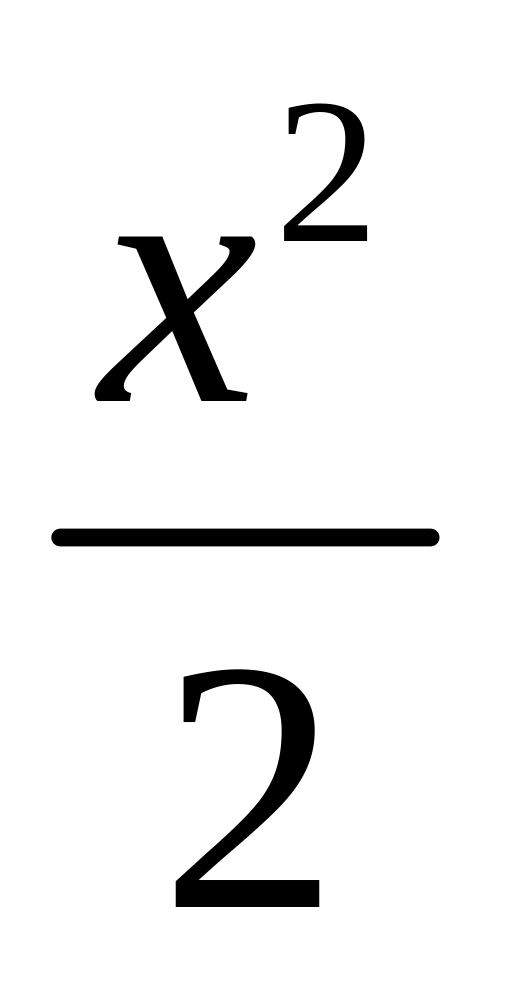
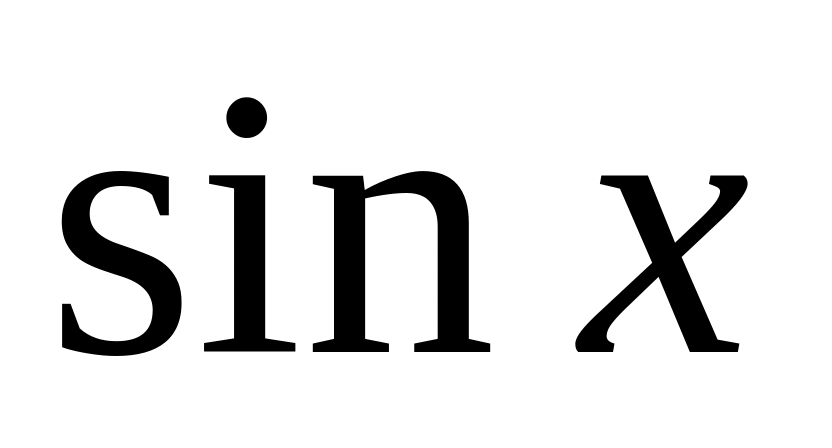
Если - первообразная функции , то функция , где С – любое действительное число, также является первообразной функции , т.к .

Теорема 1. Любые две первообразные и данной функции отличаются только на некоторую постоянную, т.е. существует число такое, что .

Доказательство. Поскольку и , то . А это означает, что . Итак, .

Следствие. Если - одна из первообразных функции , то множество всех ее первообразных имеет вид .

Теорема 2. Если функция непрерывна в области своего определения, то она имеет первообразную, определенную в этой же области.

Множество всех первообразных данной функции называется ее неопределенным интегралом (обозначается ): . Здесь - переменная интегрирования, - подынтегральная функция, - подынтегральное выражение, -знак неопределенного интеграла, - одна из первообразных функции , С – произвольная постоянная ( ) называемая постоянной интегрирования.

Например, . Множество всех первообразных подынтегральной функции представляет собой множество парабол отличающихся от первообразной параллельным переносом по оси . Таким образом, все эти параболы покрывают сплошь плоскость . При этом через каждую точку плоскости проходит только одна из парабол этого семейства первообразных.

Свойства неопределенного интеграла.

I. . II. , или .

III. . IV. .

Таблица простейших неопределенных интегралов.

1. , . 7. .

2. . 8. .

3. . 9. , .

4. , . 10. , .

5. . 11. .

6. . 12. .

Разложение подынтегральной функции на слагаемые.

Представляя подынтегральную функцию в виде алгебраической суммы отдельных слагаемых, можно воспользоваться свойством IV и проинтегрировать каждое слагаемое отдельно, используя в дальнейшем табличные формулы.

1.1). .

1.2).

.

1.3).

.

Введение функции под знак дифференциала.

Этот наиболее часто употребляемый прием заключается в следующем преобразовании

. При этом, как правило, используется одно из следующих соотношений: , , , , ,

, , , , .

1.4). .

1.5). .

1.6). .

1.7). .

Метод подстановки.

Упрощение интеграла достигается введением новой независимой переменной .

Замена позволяет преобразовать исходный интеграл к следующему виду:

, т.к. .

1.8). . Чтобы избавиться от иррациональности, используем замену переменной

. Т.к. , то

.

1.9). . Найдем область определения подынтегральной функции .

. Отсюда замена переменной имеет вид , а .

И, т.к. , то

.

Здесь .

1.10). . Используем замену переменной . Тогда . Следовательно,

.

Интегрирование по частям.

Если и - непрерывно дифференцируемые функции, то, поскольку , справедлива следующая формула , использование которой называют интегрированием по частям.

11.11). . Здесь .

1.12). = .

Последний интеграл вычислим отдельно, вторично применяя интегрирование по частям.

. Итак, окончательно

получаем .

Задания для самостоятельного решения

1.1. . 1.8. . 1.15. . 1.22. .

1.2. . 1.9. . 1.16. . 1.23. .

1.3. . 1.10. . 1.17. . 1.24. .

1.4. . 1.11. . 1.18. . 1.25. .

1.5. . 1.12. . 1.19. . 1.26. .

1.6. . 1.13. . 1.20. . 1.27. .

1.7. . 1.14. . 1.21. . 1.28. .

Ответы:

1.1. . 1.8. . 1.15. . 1.22. .

1.2. .1.9. . 1.16. . 1.23. .

1.3. . 1.10. . 1.17. . 1.24. .

1.4. . 1.11. . 1.18. .

1.25. .

1.5. .1.12. . 1.19. . 1.26.

.

1.6. . 1.13. . 1.20. . 1.27. .

1.7. . 1.14. . 1.21. . 1.28. .

Интегрирование рациональных выражений

Рассмотрим интеграл от рациональной дроби , в которой степень многочлена в числителе не меньше степени многочлена в знаменателе. Деление с остатком числителя на знаменатель позволяет представить эту подынтегральную функцию в виде суммы многочлена, как целой части данной неправильной рациональной дроби, и некоторой правильной рациональной дроби (степень многочлена меньше степени многочлена ).

1.13). . Подынтегральная функция здесь - это неправильная рациональная дробь.

Деление с остатком (“деление в столбик”) позволяет выделить ее целую часть и представить в виде: . А исходный интеграл вычисляется как разность двух интегралов.

.

Из курса алгебры известна следующая

Теорема. Любая правильная рациональная дробь может быть представлена в виде суммы простейших дробей вида

,

где ; .

1.14). . В соответствии с разложением знаменателя данной рациональной дроби по корням сама дробь по сформулированной выше Теореме представляется в виде суммы простейших дробей первого типа

.

Умножая обе части этого равенства на , получим

.

Это равенство двух многочленов выполняется тождественно для всех , а это возможно только при совпадении коэффициентов при одинаковых степенях .

Решая эту систему трех линейных уравнений с тремя неизвестными, получаем , ,

. Таким образом, подынтегральная функция представляется в виде

,

поэтому

.

1.15). . Поскольку многочлен третьей степени в знаменателе данной правильной дроби обращается в нуль при , остальные его корни находим делением этого многочлена на , и получаем следующее разложение знаменателя дроби по корням

,

в соответствии с которым по той же Теореме записываем представление подынтегральной функции в виде

.

В этом представлении множителю соответствуют две дроби второго и первого типа. Умножая обе части этого равенства на , т.е. освобождаясь от знаменателей, получим равенство двух многочленов . Составить систему

для определения коэффициентов можно двумя способами: приравнять коэффициенты при одинаковых степенях , или подставить в равенство многочленов . Итак, получаем . Следовательно,

.

1.16). . Разложение знаменателя по корням

определяет представление подынтегральной функции в виде суммы простейших дробей первого и третьего типов

.

Коэффициенты находим из тождества

,

в которое подставляем четыре различных значения . Отсюда система

,

имеющая решение . Таким образом, исходный интеграл представлен в виде суммы следующих интегралов:

.

Последний интеграл в правой части равенства вычислим выделяя в числителе производную

знаменателя и выделяя полный квадрат в знаменателе второго из следующих интегралов:

.

Окончательный ответ выглядит так

.

Замечание. При вычислении интеграла были продемонстрированы два основных приема, используемых для интегрирования функций, содержащих квадратный трехчлен, например, интегралов от простейших дробей третьего типа: . А именно: выделение в числителе производной знаменателя и выделение полного квадрата в знаменателе. В том случае, когда квадратный трехчлен в знаменателе имеет действительные корни, следует пользоваться тем, что подынтегральная функция разлагается на две простейшие дроби первого типа.

Интегрирование простейших иррациональностей

Интегралы вида , где подынтегральная функция рациональна относительно переменной интегрирования и различных радикалов из . Обозначим через наименьшее общее кратное всех показателей . Тогда рассматриваемый интеграл сводится к интегралу от рациональной функции (рационализируется) введением новой переменной

.

1.17). . Обозначим . Тогда , и =

.

1.18). . Обозначим . Тогда

.

Интегрирование тригонометрических функций

Интегралы вида рационализируются универсальной тригонометрической подстановкой: . При этом используются формулы, выражающие синус и косинус через тангенс половинного аргумента

.

Кроме того, при замене переменной в этом интеграле учитываем, что .

Рационализация с помощью универсальной подстановки иногда приводит к громоздким подынтегральным функциям. В некоторых частных случаях эффективнее использовать подстановки или .

1.19).

. В этом примере использована универсальная подстановка.

1.20). . Здесь удобно выполнить замену . И, так как , то

.

В интегралах вида , если и - четные положительные числа, используются формулы понижения степени: . Если же или - нечетное число, интеграл находят, отделяя от нечетной степени один множитель.

1.21). =

. Здесь .

1.22). . Обозначив, , получим

. Здесь .

Интегралы вида находятся с помощью тригонометрических формул: ,

, .

1.23). .

Задания для самостоятельного решения

1.29. . 1.36. . 1.43. .

1.30. . 1.37. . 1.44. .

1.31. . 1.38. . 1.45. .

1.32. . 1.39. . 1.46. .

1.33. . 1.40. . 1.47.

1.34. 1.41. . 1.48. .

1.35. . 1.42. . 1.49. .

Ответы.

1.29. 1.36. . 1.43. .

.

1.30. . 1.37. . 1.44. .

1.31. . 1.38. . 1.45. .

1.32. .1.39. . 1.46. .

1.33. . 1.40. . 1.47.

1.34. . 1.41. . 1.48. .

1.35. . 1.42. . 1.49. .

Определенный интеграл.

Функция определена и ограничена на отрезке . Произвольно выбранными точками

разобьем этот отрезок на элементарных отрезков , , длина каждого из которых равна . В каждом из этих элементарных отрезков произвольно выберем точку , . Сумма вида

называется -ой интегральной суммой функции на отрезке . Если на , то - площадь ступенчатой фигуры. Обозначим .

Конечный предел последовательности интегральных сумм при и называется определенным интегралом от функции на отрезке и обозначается

.

Предел в этом определении не зависит от способа разбиения отрезка на элементарные отрезки и выбора в каждом из них промежуточных точек . Здесь - переменная интегрирования, - подынтегральная функция, - подынтегральное выражение, - отрезок интегрирования, и -нижний и верхний пределы интегрирования. Если определенный интеграл существует, то функцию называют интегрируемой на отрезке . В частности, непрерывность подынтегральной функции на отрезке обеспечивает ее интегрируемость на этом отрезке.

Геометрический смысл определенного интеграла. Если на , то - это площадь криволинейной трапеции – плоской фигуры, ограниченной графиком функции , осью и двумя прямыми .

Теорема. Если функция определена и непрерывна на всюду за исключением конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке.

Свойства определенного интеграла.

1. ( ). 2. .

3. . 4. .

5. 6. Если, , то .

7. Если , то . 8. .

9. Если , где , то

.

10. Если непрерывна на , то существует точка , такая, что

.

Интеграл с переменным верхним пределом. Формула Ньютона – Лейбница.

Пусть функция интегрируема на , , . Тогда функция

называется интегралом с переменным верхним пределом. Перечислим основные его свойства.

1. Если интегрируема на , то функция непрерывна для любого .

2. Если непрерывна в точке , то функция имеет производную в этой точке, и . Поэтому всякая непрерывная функция имеет первообразную.

3. Если - какая-нибудь первообразная непрерывной на отрезке функции , то справедливо равенство

,

называемое формулой Ньютона – Лейбница.

1.24). . 1.25). .

1.26). .

Замена переменной в определенном интеграле.

Допустим, что в процессе вычисления определенного интеграла производится замена переменной: , , где функция и ее производная непрерывны на отрезке , причем . Замена переменной под знаком определенного интеграла осуществляется по формуле .

1.27). . Поскольку , т.е. , эффективной будет подстановка: .

Если , то , при . Учитывая, что , осуществим замену переменной в данном определенном интеграле

= = .

Интегрирование по частям в определенном интеграле.

При необходимости интегрировать по частям в определенном интеграле соответствующая формула имеет вид .

1.28). .

Вычисление площади плоских фигур.

Используя геометрический смысл определенного интеграла, вычисляется площадь фигуры, ограниченной графиками функций , и прямыми , по формуле

.

1.29). Найти площадь, ограниченную параболой и прямой .

Решение. Решая систему данных уравнений, находим абсциссы двух точек пересечения прямой и параболы : . По приведенной выше формуле

.

Интеграл с бесконечным промежутком интегрирования (несобственный интеграл)

Пусть функция непрерывна на промежутке . Интеграл по бесконечному промежутку называется несобственным интегралом первого рода. Для вычисления этого интеграла используется формула .

Интеграл называется сходящимся, если в вышеуказанной формуле существует конечный предел , в противном случае этот интеграл называется расходящимся.

Аналогично, и

, где .

1.30). Исследовать на сходимость и, если интеграл сходится, вычислить .

По определению несобственного интеграла первого рода

. Таким образом, данный интеграл расходится.

1.31). Вычислить интеграл или установить его расходимость.

По определению . В случае и при

, т.е. существует конечный предел, значит, интеграл сходится и

. В случае и при , . Таким образом, в этом случае интеграл расходится.

Задания для самостоятельного решения

1.50 – 1.63. Вычислить интегралы.

1.64. – 1.70. Вычислить площадь плоской фигуры, ограниченной данными линиями.

1.71. – 1.77. Вычислить интегралы или установить их расходимость.

1.50. . 1.57. . 1.64. . 1.71. .

1.51. . 1.58. . 1.65. . 1.72. .

1.52. . 1.59. . 1.66. . 1.73. .

1.53. . 1.60. . 1.67. . 1.74. .

1.54. . 1.61. . 1.68. . 1.75. .

1.55. . 1.62. . 1.69. . 1.76. .

1.56. . 1.63. . 1.70. . 1.77. .

Ответы.

1.50. . 1.57. . 1.64. 10,67. 1.71. Расходится.

1.51. 1. 1.58. . 1.65. 0,42. 1.72. 1.

1.52. . 1.59. 1,57. 1.66. 1,23. 1.73. .

1.53. 2,01. 1.60. 0,57 . 1.67. 29,87. 1.74. Расходится.

1.54. 0, 33. 1.61. 1,57. 1.68. 0,50. 1.75. .

1.55. 1, 50. 1.62. -0, 25. 1.69. 2, 67. 1.76. Расходится.

1.56. 0,50. 1.63. 0,21. 1.70. 0,75. 1.77. .

Контрольная № 1. Интегрирование.

1.- 8. Вычислить неопределенные интегралы.

9. Вычислить определенный интеграл.

10. Вычислить площадь фигуры, ограниченной данными линиями.

Вариант 1.

1. . 2. . 3. . 4. . 5. .

6. . 7. . 8. . 9. . 10. .

Вариант 2.

1. . 2. . 3. . 4. . 5. .

6. . 7. . 8. . 9. . 10. .

Вариант 3.

1. .2. . 3. . 4. . 5. .

6. . 7. . 8. . 9. . 10. .

Вариант 4.

1. . 2. . 3. . 4. . 5. .

6. . 7. . 8. . 9. . 10. .

Вариант 5.

1. . 2. . 3. . 4. . 5. .

6. .7. . 8. . 9. . 10. .

Вариант 6.

1. . 2. . 3. . 4. . 5. .

6. . 7. . 8. . 9. . 10. .

Вариант 7.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. . 9. . 10. .

Вариант 8.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. . 9. . 10. .

Вариант 9.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. .9. .10. .

Вариант 10.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. .9. .10. .

Вариант 11.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. .9. .10. .

Вариант 12.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. .9. .10. .

Вариант 13.

. . 2. . 3. . 4. . 5. .

6. .7. .8. .9. .10. .

Вариант 14.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. .9. .10 .

Вариант 15.

1. . 2. . 3. . 4. . 5.

6. .7. .8. . 9. .10. .

Вариант 16.

1. . 2. . 3. . 4. .5. .

6. .7. .8. .9. .10. .

Вариант 17.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. .9. .10. .

Вариант 18.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. . 9. .10. ,

Вариант 19.

1. . 2. . 3. . 4. .5. .

6. .7. .8. . 9. .10. .

Вариант 20.

1. . 2. . 3. . 4. .5. .

6. .7. .8. . 9. .10. .

Вариант 21.

1. . 2. . 3. . 4. .5. .

6. .7. .8. . 9. .10. .

Вариант 22.

1. . 2. . 3. . 4. .5. .

6. .7. .8. . 9. .10. .

Вариант 23.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. . 9. .10. .

Вариант 24.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. . 9. . 10. .

Вариант 25.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. . 9. .10. .

Вариант 26.

1. . 2. . 3. . 4. .5. .

6. .7. .8. .9. .10. .

Вариант 27.

1. . 2. . 3. . 4. . 5. .

6. .7. .8. .9. .10. .

Вариант 28.

1. . 2. . 3. .4. .5. .

6. .7. .8. . 9. .10. .

Вариант 29.

1. . 2. . 3. . 4. .5. .

6. .7. .8. . 9. .10. .

Вариант 30.

1. . 2. . 3. .4. .5. .

6. .7. .8. .9. .10.

2. Функции нескольких переменных

Если каждой точке из некоторого подмножества пространства по некоторому правилу или закону поставлено в соответствие единственное значение переменной из множества , то говорят, что задана функция нескольких переменных ( переменных): . Подмножество называется областью определения этой функции, а - множеством ее значений.

Например, - функция двух переменных, - функция трех переменных. В этом разделе будут рассмотрены некоторые из понятий дифференциального исчисления функций двух переменных: .

Графиком функции двух переменных называется множество точек трехмерного пространства , таких, что и . Таким образом, график представляет собой поверхность - множество точек с координатами в пространстве .

2.1). Найти область определения функции . Существование этой функции обеспечивает условие , т.е. . Таким образом, областью определения данной функции является внутренность круга с центром в начале координат и радиусом 1.

Для построения поверхности – графика функции используется метод сечений этой поверхности плоскостями, параллельными координатной плоскости , т.е. системой плоскостей , где произвольное число . Пересечение поверхности с плоскостью определяется равенством .

Линией уровня функции двух переменных называется множество точек плоскости , удовлетворяющих равенству . Число здесь называют уровнем. Итак, для точек, принадлежащих одной линии уровня, функция принимает одно и то же значение, равное .

2.2). Найти линии уровня функции . Построить ее график. Линии уровня данной функции определяются уравнениями , где . Эти уравнения описывают множество концентрических окружностей в плоскости с общим центром в начале координат с радиусами . График этой функции представляет собой поверхность , называемую параболоидом.

Число называется пределом функции в точке ( ), если для любого сколь угодно малого положительного числа ( ) найдется такое положительное число ( ), что для всех точек , отстоящих от точки на расстояние меньшее, чем (такое множество точек называется -окрестностью точки : ) , выполняется неравенство . Если предел существует, то он не зависит от пути, по которому точка стремится к точке .

2.3). .

2.4). . Например, при , т.е., если точка стремится к точке по прямой , предел равен . Если же , т.е. точка стремится к точке по прямой . В этом случае предел оказывается равен . Итак, предел в этом примере не существует, так как при стремлении точки к точке по различным путям, он получается различным.

Функция называется непрерывной в точке , если

1. функция определена в точке и в некоторой ее окрестности,

2. существует конечный предел при стремлении точки к точке произвольным образом,

3. .

Функция разрывна в точке , если нарушено хотя бы одно из условий 1., 2., 3.

Функция непрерывная в любой точке некоторой области называется непрерывной в этой области

.

2.5). Функция определена во всех точках плоскости , но не в точке , поэтому разрывна в этой точке. В остальных точках плоскости она непрерывна.

2.6). Функция разрывна в точке , так как не имеет предела в этой точке.

2.7). Функция разрывна в точке , поскольку .

Теорема. Если функция непрерывна в ограниченной замкнутой области , то

1. она в этой области ограничена, т.е. существует число ( ) такое, что для всех точек выполняется неравенство ,

2. в области имеются точки, в которых функция достигает своего наименьшего и наибольшего значений.

Частные производные функции двух переменных. Полный дифференциал.

Рассмотрим функцию . Пусть - область ее определения. Зафиксируем точку . Придадим аргументам и приращения и соответственно. При этом . Тогда разности и

называются частными приращениями функции по переменным и соответственно, а разность - ее полным приращением.

Частными производными функции по переменным и называются следующие пределы разностных отношений .

Значение частной производной функции зависит от точки , в которой она вычисляется, т.е. сама по себе частная производная является функцией точки . Формулы и правила, используемые при вычислении производной функции одной переменной, справедливы также и для частных производных функции двух переменных. Главное в процессе вычисления частной производной функции по одной из ее переменных – помнить, что другая переменная при этом считается постоянной.

2.8). Вычислить частные производные функции .

, .

Частные производные, как функции тех же переменных, тоже в свою очередь могут иметь частные производные, которые называются частными производными второго порядка.

, , , ,

Смешанные производные и равны между собой, если они являются непрерывными функциями.

2.9). Вычислить частные производные второго порядка функции .

Пользуясь уже имеющимися в примере 36) частными производными первого порядка, получаем , , ,

. Как видим, .

Если функция имеет в точке непрерывные частные производные, то ее полное приращение может быт представлено в виде , где

и при . Главная линейная часть полного приращения функции называется ее полным дифференциалом , с учетом того, что для независимых переменных и .

2.10). Полный дифференциал функции записываем, следуя формуле

Производная по направлению. Градиент.

Пусть функция определена в некоторой области . Точка , - некоторое направление (вектор с началом в точке М), задаваемое единичным вектором (ортом)

, где и - косинусы углов, образуемых вектором с осями координат, называемые направляющими косинусами. При перемещении из точки в точку по направлению функция получает приращение

, называемое приращением функции в данном направлении . Пусть - величина перемещения. Предел отношения при , если он существует, называется производной функции по направлению и обозначается , или . Итак, . Производная характеризует изменения функции в направлении . При заданных направляющих косинусах производная по направлению вычисляется по формуле .

Градиентом функции в точке называется вектор , координаты которого равны соответствующим частным производным и , вычисленным в точке . Т.е. , или . Градиент, это вектор, указывающий направление наибольшего роста функции.

2.11). Вычислить производную функции в точке по направлению .

Найдем длину вектора : . Тогда . Таким образом, единичный орт вектора имеет координаты . Используя частные производные и , запишем производную по направлению в произвольной точке : . Итак, в точке эта производная оказывается равной .

2.12). Вычислить градиент функции в точке .

Градиент этой функции в произвольной точке выглядит так . В данной точке .

Экстремум функции двух переменных.