
Плоска задача теорії пружності в прямокутній системі координат.
Р озглянемо
плоску пластину до якої прикладене
зовнішнє навантаження. Будемо вважати,
що її товщина дуже мала у порівняння з
поперечними розмірами. За таких умов,
розглядуване тіло є дуже тонка розтягнута
плівка. Виділимо нескінченно малий
прямокутний елемент пластини (рис. 4.1).
На його гранях, в загальному випадку,
виникають напруження σx,
σy,
τxy
= τyx
= τ.
На бокових (заштрихованих) гранях цього
елемента напруження відсутні: σz
= 0, τxz
= 0, τyz
=0. Припустимо, що ці напруження дорівнюють
нулю і у внутрішніх точках елемента.
Описуваний стан називають узагальненим
плоским
напруженим станом елемента.
Він характеризується тим, що дві
паралельні грані нескінченно малого
елемента, вільні від напружень. Напруження
σx,
σy,
τ
при цьому рівномірно розподілені за
товщиною пластини.
озглянемо
плоску пластину до якої прикладене
зовнішнє навантаження. Будемо вважати,
що її товщина дуже мала у порівняння з
поперечними розмірами. За таких умов,
розглядуване тіло є дуже тонка розтягнута
плівка. Виділимо нескінченно малий
прямокутний елемент пластини (рис. 4.1).
На його гранях, в загальному випадку,
виникають напруження σx,
σy,
τxy
= τyx
= τ.
На бокових (заштрихованих) гранях цього
елемента напруження відсутні: σz
= 0, τxz
= 0, τyz
=0. Припустимо, що ці напруження дорівнюють
нулю і у внутрішніх точках елемента.
Описуваний стан називають узагальненим
плоским
напруженим станом елемента.
Він характеризується тим, що дві
паралельні грані нескінченно малого
елемента, вільні від напружень. Напруження
σx,
σy,
τ
при цьому рівномірно розподілені за
товщиною пластини.
Рівняння теорії пружності значно спрощуються для випадку плоского напруженого стану, оскільки задача зводиться до визначення тільки двох змінних. При плоскому напруженому стані, в пружному тілі, переміщення відбуваються тільки паралельно площині xOy:
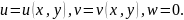
Підставляючи ці складові переміщень в геометричні співвідношення Коші (4.3), отримаємо:
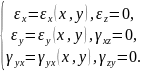 (4.12)
(4.12)
Незважаючи на те, що в напрямку осі Oz відсутні лінійні деформації, в цьому напрямку діє напруження σz. При цьому елемент перебуває в стані плоскої деформації. Єдина відмінність останнього від узагальненого плоского напруженого стану це те що σz ≠0. Напруження σz залежать від напружень, що діють в площині xOy. Дійсно, з третьої формули закону Гука (4.5) за відсутності деформації εz, отримаємо:
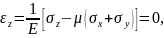
звідки
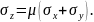 (4.13)
(4.13)
Це ж рівняння можна записати наступним чином:

Зважаючи на сказане запишемо основні рівняння теорії пружності для випадку плоского напруженого стану.
Диференціальні рівняння рівноваги (4.1) набувають вигляду:
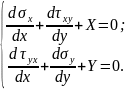 (4.14)
(4.14)
Оскільки на боковій поверхні в усіх точках направляючий косинус n = 0, то з рівнянь умов на поверхні (4.2) залишаються тільки два:
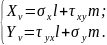 (4.15)
(4.15)
Шість геометричних співвідношень Коші (4.3) зводяться до трьох:
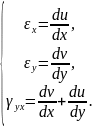 (4.16)
(4.16)
З шести рівнянь нерозривності деформацій (4.4) залишається лише тільки одне, а інші перетворюються на тотожність:
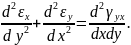 (4.17)
(4.17)
З шести формул закону Гука (4.5) залишаються тільки три, які з врахуванням виразів (4.12), (4.13) набувають вигляду :
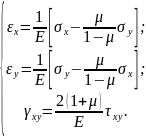 (4.18)
(4.18)
Введемо
позначення. Нехай
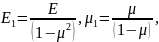 тоді
формули (4.18) набувають вигляду:
тоді
формули (4.18) набувають вигляду:
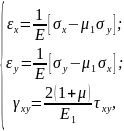 (4.19)
(4.19)
при цьому значення коефіцієнта пропорційності в третьому рівнянні не змінюється:
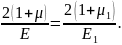
Узагальнений плоский напружений стан.
Як згадувалося раніше узагальнений плоский напружений стан відрізняється від стану плоскої деформації тим, що для першого випадку σz = 0. Якщо за допомогою узагальненого закону Гука (4.5) перейти від напружень до деформацій, то отримаємо:
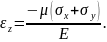
Тобто відносна деформація в напрямку осі z буде відмінною від нуля. Відповідно основа пластинки буде дещо викривлятися.
За цих припущень основні рівняння плоскої деформації – диференціальні рівняння рівноваги (4.14), умови на поверхні (4.15), геометричні співвідношення Коші (4.16) та рівняння нерозривності деформацій (4.17) – зберігають такий же вигляд і в задачі про узагальнений плоский напружений стан. Формули узагальненого закону Гука (4.5) набувають вигляду:
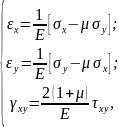 (4.20)
(4.20)
Останні відрізняються від закону Гука (4.19) для плоскої деформації тільки значенням пружних сталих μ, Е. Відповідно, при розв’язанні задач по плоскій деформації та плоскому напруженому стану можна користуватися одніми і тими ж самими рівняннями та поєднувати їх в одну: плоску задачу теорії пружності.
