Продолжение. 14.11.11.

Пример: 3. Общее решение ур-ние уу''-2у''=0. Решение: Полагая y'=z(y) и учитывая, что y''=z*dz/dy получаем zy*dz/dy-2z²=a. Это ур-ние 1-го порядка с разделяющимися переменными. Приводя его к виду dz/z=2dy/y и интегрируя, имеем ln│z│=zln│y│+ln│C₁│, откуда z=C₁y². Учитывая, что z=dy/dx, находим dy/y'=C₁dx, откуда получаем искомое решение -1/y=C₁x+C₂ или y=-1/(C₁x+C₂). При сокращении на z было потеряно решение ур-ния z=y''=0, т.е. y=C=const. В данном случае оно содержится в общем решении, т.к. получается из него при C₁=0 (за исключением решения у=0). Решение ур-ний вида: у⁽ⁿ⁾=G(x). (везде заменяем G на f), а G в скобках - (G) Это ур-ние легко решается. Действительно, интегрируя последовательно n раз, получаем: y^(n-1)=∫G(x)dx+C₁, y^(n-2)=∫[G(x)dx+C₁]dx+C₂=∫dx∫G(x)dx+C₁x+C₂ y=∫dx∫dx . . . ∫G(x)dx+C₁*x^n-1/(n-1)!+ C₂*x^n-2/2(n-2)! + . . . + C_n, (z) где С₁, С₂, . . ., С_n – произвольные постоянные. Функция (z) и является общим решением ур-ния (G). Пример 4: Найти общее решение ур-ия 3-го порядка у'''=С^х и выделить из него частное решение, удовлетворяющее следующим начальным условиям: у│=0, у'│=0, у''│ =1 х=0 х=0 х=0

Линейные ур-ния с постоянными коэффициентами.

Опр. Линейным дифференциальным ур-ем 2-го порядка наз-ся ур-ние вида у''+Р(х)у'+q(x)y=f(x), где у – искомая ф-ция, Р(х), q(x) и f(x) - известные функции непрерывные на некотором интервале (а,в). Если f(x)=0, то ур-ние наз-ся линейным однородным ур-нием. В этом разделе мы рассмотрим важный и распространенный случай, когда в ур-нии вида ф-ции Р(х) и q(x) – постоянные величины. Ур-ния такого вида наз-ся линейными ур-ниями с постоянными коэффициентами . Итак, мы рассмотрим ур-ние вида y''+py'+qy=f(x), где p и q – вещественные числа. Далее мы будем иметь дело только с ур-ями такого типа. Линейное однородное ур-ние. у''+py'+qy=0, где p и q – вещественные числа. Линейные дифференциальные ур-ния второго порядка может иметь множество решений. Однако среди них выделяют базисные решения, по которым строится общее решение ур-ния. Таких решений для ур-ния второго порядка два – каков и порядок ур-ния. Будем искать решение ур-ния в виде у=е^kx, где k – некоторое число. Подставляя эту ф-цию в ур-ние, получаем k²e^kx+pke^kx+qe^kx+qe^kx+qe^kx=0. Сокращая оби части равенства на е^kx, получаем квадратное ур-ние относительно k: k²+pk+q=0. Ур-ние наз-ся характеристическим ур-нием для дифференциального уравнения. Вид общего ур-ния существенно зависит от того, какие корни имеет характеристическое ур-ние. Обозначим эти корни через k₁ и k₂ . Если корни характеристического ур-ния вещественные и k₁ ≠k₂ , то общее решение однородного дифференциального ур-ния имеет вид y=c₁e^k1x+C₂e^k2x. Если корни ур-ния вещественные и равные (k₁=k₂=k), то общее решение ур-ия имеет вид y=C₁e^kx+C₂xe^kx. Если корни характеристического ур-ния комплексные (k₁=a+bi ; k₂=a-b ; где i=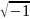 - мнимая единица, а и в – вещественные числа, то общее решение имеет вид: y=e^ax(C₁cosbx+C₂sinbx), где а=-р/2, в= q-p²/4. Во всех трех случаях С₁ и С₂ – произвольные постоянные. Пример: (забил)

21.11.11.

у''-6у'+9=0. Решение: Составим характеристическое ур-ие: К²-6К+9=0 или (k-3)²=0. Оно имеет кратный корень к=3 ; Следовательно, общее решение данного однородного ур-ия имеет вид: у=е^3х(С₁+С₂) Пример: у''-2у'+2у=0. Решение: Соответствующее характеристическое ур-ие: К²-2К+2=0. Имеет дискриминант, равный -1, и значит, комплексно-сопряженные корни К₁=1+I, K₂=1-j, где i=sqrt-1 – мнимая единица. Следовательно, общее решение данного ур-ия дается формулой: у=е^х(С₁sinx+C₂cosx).