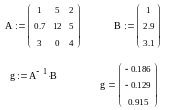Розв’язок систем нелінійних рівнянь: способи організації, пояснення приклади.
Розглянемо розв’язок системи N нелінійних рівнянь з М невідомими. Рівнянь може бути як більше, так і менше числа змінних. Для розв’язку систем є спеціальний обчислювальний блок, що складається з трьох частин, які йдуть послідовно один за одним:
- Given - ключове слово;
- система, записана логічними операторами у вигляді рівностей і, можливо, нерівностей;
- Find(xі,... ,хm) - вбудована функція для розв’язку системи щодо змінних xі,...,хm.
Вставляти логічні оператори потрібно користуючись панеллю інструментів Boolean (булеві оператори). З клавіатури логічний знак рівності вводиться сполученням клавіш <Ctrl>+<=>. Блок Given / Find використовує для пошуку розв’язку ітераційні методи.
Спочатку зробимо перетворення системи, визначивши рівняння через функції Y(x) та X(y). Далі будуємо графіки цих функцій з метою наближеного визначення коренів рівняння. Як бачимо, система має два розв'язки.
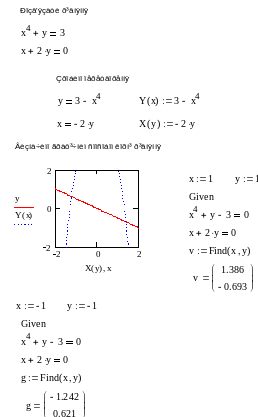
Поки що ми розглянули приклад системи з двох рівнянь і таким же числом невідомих, що зустрічається найбільш часто. Але число рівнянь та невідомих може і не збігатися. Більш того, в обчислювальний блок можна додати додаткові умови у вигляді нерівностей. Наприклад, введення обмеження на пошук тільки негативних значень аргументу х у розглянутому вище прикладі 5.1, приведе до отримання іншого розв’язку, як це показано в прикладі 5.2.
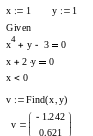
Програмування в Mathcad - розгалуження: призначення, способи створення і застосування, приклади.
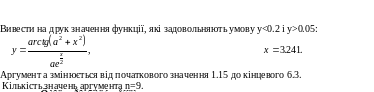Циклічна
Спочатку введемо в документ вхідні дані та обчислимо крок зміни аргументу а – а3.
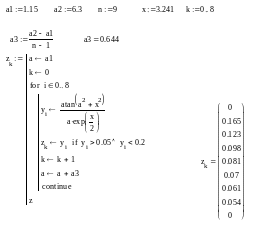
В цій програмі згідно умови задачі, виводяться у вигляді масиву zk тільки ті елементи масиву yi , які задовольняють умову.
Циклічна структура з вкладеними циклами наведена в прикладі 7.17.
Вкладені цикли
Обчислити всі значення функції с, що має два змінних аргументи φ та d:
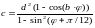
6.35 > φ> 7.40 Δφ =0.15
10.4 ≥ d ≥ 17.9 Δd = 2.5
Спочатку обчислимо кількість циклів по кожній змінній:
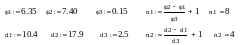
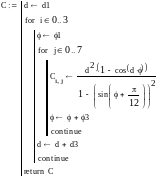
Приклад 7. 17 Програми з вкладеними циклами
Результатом обчислень в програмі є матриця Сi,j розміром 4 рядки та 8 стовпців.
В прикладі 7.18 наведені програми обробки векторів.
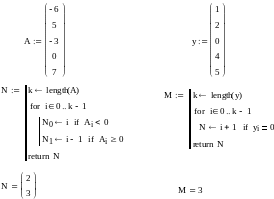
Розв’язок систем лінійних алгебраїчних рівнянь: пояснення приклади
Центральним питанням обчислювальної лінійної алгебри є розв’язок систем лінійних алгебраїчних рівнянь (СЛАУ), тобто систем рівнянь виду ( як приклад розглядаємо систему з трьох рівнянь з трьома невідомими):
(1)
У матричній формі СЛАУ записується в еквівалентному вигляді:
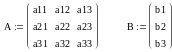(2)
СЛАУ має єдиний розв’язок, якщо матриця А є не виродженою, тобто її визначник не дорівнює нулю. У Mathcad СЛАУ можна розв’язати як у більш наочній матричній формі (1), так і в більш зручній для запису та наочній формі (2). Для першого способу варто використовувати вбудовану функцію Isolve , а для другого - обчислювальний блок Given / Find. Функція Isolve має таку структуру:
- lsolve (А,B) – розв’язок системи лінійних рівнянь;
А - матриця коефіцієнтів системи;
B - вектор правих частин.
Застосування функції Isolve показано в прикладі 5.6, а обчислювального блоку Given / Find в прикладі 5.7.
Вбудовану функцію Isolve допускається застосовувати і при символьному розв’язку СЛАУ.
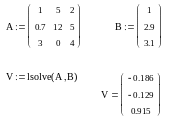
Розв’язок СЛАУ матричним способом за допомогою функції Isolve
У випадку розв'язку системи нелінійних рівнянь з допомогою блоку Given / Find , її розв’язується точно так само, як і системи нелінійних рівнянь. Треба не забувати, що в цьому випадку застосовуються чисельні методи розв’язку, які вимагають перед записом блоку привласнювання всім невідомим початкових значень (це зроблено в першому рядку прикладу 5.7). Вони можуть бути довільними, тому що розв’язок СЛАУ з не виродженою матрицею єдиний. Невідомі в цьому випадку позначені змінними x, y та z
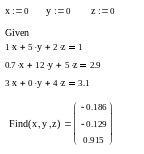
Приклад 5.7 Розв’язок СЛАУ за допомогою обчислювального блоку
Розв’язок СЛАУ можна також отримати за допомогою обчислювального блоку з функцією Minerr, а також використовуючи в матричному варіанті розв’язку оберненої матриці (приклад 5.8).
