Ориентированный граф
Смешанный граф
Изоморфные графы
№21.Основные понятия теории графов
Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины, прилегающие к одному и тому же ребру, называются смежными. Если ребра ориентированны, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом. Если ребра не имеют ориентации, граф называется неориентированным.
Путь в ориентированном графе — это последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей.
№22.Операции над Графами.
Объединение графов G1
и G2 , обозначаемое как
![]() ,
представляет такой граф
,
представляет такой граф
![]() ,
что множество его вершин является
объединением Х1 и Х2 , а
множество ребер – объединением A1
и A2
,
что множество его вершин является
объединением Х1 и Х2 , а
множество ребер – объединением A1
и A2
Пересечение графов G1
и G2 , обозначаемое как
![]() ,
представляет собой граф
,
представляет собой граф
![]() .
.
Кольцевая сумма двух графов G1
и G2 , обозначаемая как
![]() ,
представляет собой граф G5 ,
порожденный на множестве ребер
,
представляет собой граф G5 ,
порожденный на множестве ребер
![]() .
.
Удаление вершины. Если хi -вершина графа G = (X, A), то G–хi -порожденный подграф графа G на множестве вершин X–хi , т. е. G–хi является графом, получившимся после удаления из графа G вершины хi и всех ребер, инцидентных этой вершине.
Удаление ребра или удаление дуги. Если ai - дуга графа G = (X, A), то G-ai – подграф графа G, получающийся после удаления из G дуги ai .
Стягивание. Под стягиванием подразумевают операцию удаления дуги или ребра и отождествление его концевых вершин.
№23.Маршруты, цепи, циклы.
Маршрут в графе путь, ориентацией дуг которого можно пренебречь. Цепь маршрут, в котором все ребра попарно различны.
Пример (цепь). Маршрут a,{a,b},b,{b,c},c,{c,a},a,{a,d},d в первом графе из примера 1 является цепью, но не является простой цепью. Цикл замкнутый маршрут, являющийся цепью.
№24.Способы задания графов.
Графы могут задаваться следующими способами:
1. Геометрическим способом – рисунки, схемы, диаграммы,
2. Алгебраическим способом – перечислением вершин и ребер,
3. Табличным способом.
4. Матричным способом.
№25. Эйлеровы и Гамильтоновы графы.
Гамильтонов граф — граф, в котором есть гамильтонов цикл. Гамильтонов цикл — простой цикл в графе, содержащий все вершины графа ровно по одному разу
Эйлеров граф — это граф, в котором существует цикл, содержащий все рёбра графа по одному разу (вершины могут повторяться).
Эйлерова цепь (или Эйлеров цикл) — это цепь ( цикл), которая содержит все рёбра графа (вершины могут повторяться).
№26.Алгоритм поиска кратчайшего пути в графе. Алгоритм Дейкстры.
Алгоритм Дейкстры- Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании и технологиях, например, его использует протокол OSPF для устранения кольцевых маршрутов.
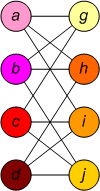
№27. Изоморфные Графы.
Изоморфизм. Два графа называются изоморфными, если существует перестановка вершин, при которой они совпадают. Иначе говоря, два графа называются изоморфными, если существует взаимно-однозначное соответствие между их вершинами и рёбрами, которое сохраняет смежность и инцидентность (графы отличаются только названиями своих вершин).
Граф G Граф H Изоморфизм между графами
G и H Подстановка изоморфизма f
№28.Раскраска Графов. Хроматическое число.
Раскрашивать можно как ребра графа, так и вершины. Коснемся сначала задачи о раскраске вершин,. при этом считаем, что граф не ориентирован и не является мультиграфом.
Задача. Раскрасить вершины графа так, чтобы любые две смежные вершины были раскрашены в разные цветы, при этом число использованных цветов должно быть наименьшим. Это число называется хроматическим (цветным) числом графа, будем его обозначать = (G) (если G – данный граф). Если число k , то граф называется k-раскрашиваемым.
Хроматическое число графа — минимальное количество цветов, требуемое для раскраски вершин графа, при которой любые вершины, соединенные ребром, раскрашены в разные цвета.
№29.Дать определение графа вида «дерево» и «лес»
Лес — неориентированный граф без циклов. Компонентами связности леса являются деревья. Дерево — связный граф, не содержащий циклов.
№30.Планарные и плоские Графы
Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер.
Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его вершины — это точки плоскости, а ребра — линии на ней. Области, на которые граф разбивает поверхность, называются гранями. Плоский граф — граф, уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу.
№31. Понятия о функции алгебры логики. Существенные и несущественные переменные.
Булева функция (функция алгебры логики) — функция, определённая на множестве упорядоченных наборов из нулей и единиц и принимающая на каждом из этих наборов значение 0 или 1.
Переменная xi функции f (x1, …, xn) называется существенной, если существуют такие два набора из нулей и единиц, различающиеся только в i-й компоненте, что функция f на этих наборах принимает различные значения.
№32.Элементарные функции алгебры логики.
Двоичной, булевой функцией от набора двоичных переменных называется функция, результатом которой могут быть только значения 0 и 1. Любую булеву функцию можно задать с помощью таблицы, в которой всем возможным наборам значений двоичных переменных сопоставлены соответствующие им значения функции. Такая таблица называется таблицей истинности, поскольку она определяет истинность или ложность сложного высказывания в зависимости от истинности или ложности составляющих высказываний.
№33.Свойства логических функций.
Коммутативность
Идемпотентность
Ассоциативность
Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:
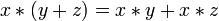 ,
,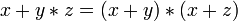 ,
,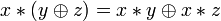 .
.
Законы де Мо́ргана:
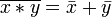 ,
,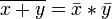 .
.
Законы поглощения:
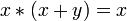 ,
,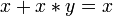 .
.
№34.Реализайия функций формулами. Принцип двойственности.
Так же, как составные высказывания строятся из более простых, с помощью логических операций, можно комбинировать булевы переменные с помощью булевых операций, получая булевы выражения, которые называются формулами.Всякой формуле однозначно соответствует некоторая функция, при этом говорят, что формула реализует функцию.
Принцип двойственности в абстрактной теории множеств. Пусть дано множество М. Рассмотрим систему всех его подмножеств А, В, С и т. д. Справедливо следующее предложение: если верна теорема о подмножествах множества М, которая формулируется лишь в терминах операций суммы, пересечения и дополнения, то верна также и теорема, получающаяся на данной путём замены операции суммы и пересечения соответственно операциями пересечения и суммы, пустого множества Λ — всем множеством М, а множества М — пустым множеством Λ.
№35.Разложение Булевых функций по переменным.
Рассмотрим вопрос представления n-местной булевой функции f(x1,x2,…,xn) какой-нибудь формулой алгебры высказываний.
Введем обозначение
![]() ,
где
,
где
![]() -
параметр, равный 0 или 1.
-
параметр, равный 0 или 1.
Очевидно, что
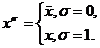
Теорема . Каждую функцию алгебры логики f(x1,x2,…,xn) при любом m(1£m£n) можно представить в следующей форме:
![]() (1),
(1),
где дизъюнкция берется по всевозможным
наборам значений переменных
![]() .
.
№36. Совершенная Дизъюнктивная Нормальная Форма
СДНФ (Совершенная Дизъюнктивная Нормальная Форма) — это такая ДНФ, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных конъюнкций
в каждой конъюнкции нет одинаковых пропозициональных букв
каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причем в одинаковом порядке.
№37. Совершенная Конъюнктивная Нормальная Форма
СКНФ (Совершенная Конъюнктивная Нормальная Форма) — это такая КНФ, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных дизъюнкций
в каждой дизъюнкции нет одинаковых пропозициональных букв
каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
№38. Полнота системы булевых функций.
Полные системы функций
Множество A функций алгебры логики называется полной системой, если замыкание этого множества совпадает с множеством всех функций. (В частности, для двузначной логики [A] = P2.) Другими словами, должна быть возможность любую функцию алгебры логики выразить формулой с использованием функций множества A.
Критерий Поста формулирует необходимое и достаточное условие полноты системы булевых функций:
Система булевых функций полна тогда и только тогда, когда она не содержится целиком ни в одном из классов T0, T1, S, M, L.
№39. Полиномы Жегалкина.Пример.
Каждая булева функция представляется в виде полинома Жегалкина единственным образом.
Метод неопределенных коэффициентов. Пусть P(X1,X2 ... Xn) - искомый полином Жегалкина, реализующий заданную функцию f(X1,X2 ... Xn). Запишем его в виде
P=C0⊕C1X1⊕C2X2⊕ ... ⊕CnXn⊕C12X1X2⊕ ... ⊕C12 ... nX1X2 ... Xn
Найдем коэффициенты Ck. Для этого последовательно придадим переменным X1,X2 ... Xn значения из каждой строки таблицы истинности. В итоге получим систему из 2n уравнений с 2n неизвестными, имеющую единственное решение. Решив ее, находим коэффициенты полинома P(X1,X2 ... Xn).
Пример. Построить полином Жегалкина функции f(X,Y)=X→Y
Решение.
Запишем искомый полином в виде:
P=C0⊕C1X⊕C2Y⊕C12XY
Пользуясь таблицей истинности
X 0 0 1 1
Y 0 1 0 1
X→Y 1 1 0 1
получаем, что
f(0,0)=P(0,0)=C0=1
f(0,1)=P(0,1)=C0⊕C2=1
f(1,0)=P(1,0)=C0⊕C1=0
f(1,1)=P(1,1)=C0⊕C1⊕C2⊕C12=1
Откуда последовательно находим, C0=1, C1=1, C2=0, C12=1
Следовательно: x→y=1⊕X⊕XY.
№40. Понятие замыкания и замкнутого класса.
Замкнутый класс в теории булевых функций — такое множество P функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: [P] = P. Другими словами, любая функция, которую можно выразить формулой с использованием функций множества P, снова входит в это же множество.
Любое множество является подмножеством своего замыкания:
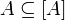 .
.Замыкание подмножества является подмножеством замыкания:
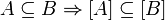 .
Следует
заметить, что из строгого вложения
множеств следует лишь нестрогое вложение
их замыканий:
.
Следует
заметить, что из строгого вложения
множеств следует лишь нестрогое вложение
их замыканий:
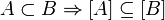 .
.Многократное применение операции замыкания эквивалентно однократному: [[A]] = [A].
№41. Класс Т0.
Т0 – это набор всех тех логических функций, которые на нулевом наборе принимают значение 0 (Т0 – это класс функций, сохраняющих 0).
Класс Т0 функционально замкнут.
№ 42. Класс Т1.
Т1 – это набор всех логических функций, которые на единичном наборе принимают значение 1 (Т1 – это класс функций, сохраняющих единицу) (заметим, что число функций от п переменных принадлежащих классам Т0 и Т1 равно 22n-1).
Класс Т1 функционально замкнут.
№ 43. Класс S.
S – класс всех самодвойственных функций. Класс S является функционально замкнутым. Доказательство следует из принципа двойственности.
№44. Класс M.
Класс M монотонных функций замкнут.
Свойство:
У монотонных функций сокращенная ДНФ не содержит отрицаний переменных, то
есть все простые импликанты не содержат отрицаний.
№45 Класс L.
Класс всех линейных функций замкнут.
Доказательство.
Пусть L – класс линейных функций (так и будем обозначать в дальнейшем).
L = {а0+a1x1+a2x2+…+anxn}
Подставим вместо переменной x в одну из функций функцию y такого же вида.
Получим L = [L].
№46-
№47. Теорема Поста.
Для того чтобы некоторый набор функций K был полным, необходимо и достаточно, чтобы в него входили функции, не принадлежащие каждому из классов T0, T1, L, M, S.
В соответствии с теоремой Поста набор функций будет полным тогда и только тогда, когда в каждом столбце таблицы Поста имеется хотя бы один минус. Таким образом, из приведенной таблицы следует, что данные 4 функции образуют полный набор, но эти функции не являются базисом. Из этих функций можно образовать 2 базиса: f3, f1 и f3, f2. Полными наборами будут любые наборы содержащие, какой-либо базис.
№48. Понятие ДНФ и проблема минимизации булевых функций.
Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции
элементарных конъюнкций.
Дизъюнктивная нормальная форма называется минимальной, если она содержит наименьшее
число букв среди всех ДНФ, эквивалентных ей
№49. Индекс простоты. Аксиомы
Индексом простоты называется функция L(R) ,определённая на множестве всех ДНФ и удовлетворяющая свойствам: неотрицательности, монотонности, выпуклости и инвариантности.
№50. Алгоритм упрощения ДНФ. Тупиковая ДНФ.
Дизъюнктивная нормальная форма называется тупиковой, если отбрасывание любой конъюнкции или буквы приводит к ДНФ, которая не эквивалентна исходной ДНФ. Определенные выше ДНФ − сокращенная, тупиковая и минимальная находятся в следующем
соотношении. Тупиковая ДНФ получается из сокращенной путем удаления некоторых слагаемых.
Минимальная ДНФ находится среди тупиковых.
№51 Алгоритм построения Сокращенной ДНФ.
Дизъюнкция всех простых импликант функции называется сокращенной ДНФ.
1)Строим СКНФ
2)Раскрываем в СКНФ все скобки и упрощаем ее.
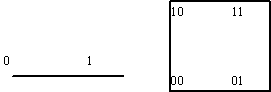
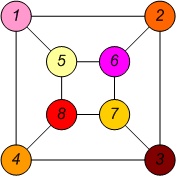
№52.Геометрическое представление Булевых функций.
При геометрическом способе булева функция f(х1,..., xn) задается с помощью n-мерного куба. В геометрическом смысле каждый двоичный набор есть n-мерный вектор, определяющий точку n-мерного пространства. Исходя из этого, все множество наборов, на которых определена функция n переменных, представляется вершинами n-мерного куба. Отмечая точками вершины куба, в которых функция принимает единичные (либо нулевые) значения, получим геометрическое представление функции. Например, булева функция, заданная табл.1, геометрически представляется 3-мерным кубом (рис. 1.в).
|
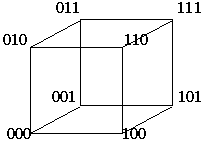
а) n=1 б) n=2 в) n=3
а) одной переменной: б) двух переменных; в) трех переменных.
№53.Символы и формулы исчисления высказываний.
Базовыми понятиями логики высказываний являются пропозициональная переменная — переменная, значением которой может быть логическое высказывание, — и (пропозициональная) формула, определяемая индуктивно следующим образом:
Если P — пропозициональная переменная, то P — формула.
Если A — формула, то
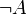 —
формула.
—
формула.Если A и B — формулы, то
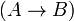 ,
,
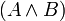 и
и
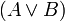 —
формулы.
—
формулы.Других соглашений нет.
Знаки
![]() и
и
![]() (отрицание,
конъюнкция,
дизъюнкция
и импликация)
называются пропозициональными
связками. Подформулой
называется часть формулы, сама являющаяся
формулой. Собственной подформулой
называется подформула, не совпадающая
со всей формулой.
(отрицание,
конъюнкция,
дизъюнкция
и импликация)
называются пропозициональными
связками. Подформулой
называется часть формулы, сама являющаяся
формулой. Собственной подформулой
называется подформула, не совпадающая
со всей формулой.
Законы де Моргана:
1)
![]() ;
;
2)
![]() ;
;
Закон контрапозиции:
![]() ;
;
Законы поглощения:
1)
![]() ;
;
2)
![]() ;
;
Законы дистрибутивности:
1)
![]() ;
;
2)
![]() .
.
№54.Аксиомы исчисления высказываний.
Аксиомы
I
1.
![]()
![]() .
.
2.
![]()
![]()
![]()
![]() .
.
II
1.
![]()
![]() .
.
2.
![]()
![]() .
.
3.
![]()
![]()
![]()
![]() .
.
III
1.
![]()
![]() .
.
2.
![]()
![]() .
.
3.
![]()
![]()
![]()
![]() .
.
IV
1.
![]()
![]() .
.
2.
![]()
![]() .
.
3. .
№55.Правила вывода
Правила вывода
(![]()
![]() - знак выводимости)
- знак выводимости)
Правило подстановки
![]()
![]()
![]()
где
![]()
![]() -
формула, полученная из p путем
подстановки формулы q вместо
переменной x.
-
формула, полученная из p путем
подстановки формулы q вместо
переменной x.
Правило заключения
![]()
![]()
![]()
![]()
№56.Теорема дедукции.
![]() выводима
из
выводима
из
![]() ,
если ее можно вывести, используя только
правила заключения из этих формул и
всех истинных формул.
,
если ее можно вывести, используя только
правила заключения из этих формул и
всех истинных формул.
Будем
это обозначать так:
![]() .
Обозначение
.
Обозначение
![]() означает
означает
![]() можно вывести из аксиом без привлечения
каких-либо дополнителных формул, т.е.
- истинная формула.
можно вывести из аксиом без привлечения
каких-либо дополнителных формул, т.е.
- истинная формула.
Теорема
дедукции: Если
![]() выводима из
выводима из
![]() ,
то
,
то
![]() - истинная формула и наоборот.
- истинная формула и наоборот.
№57.Эквивалентные формулы. Интерпретация формул.
Формулы
![]() и
и
![]() будем записывать
будем записывать
![]() .
Знак ~ не является символом ИВ.
.
Знак ~ не является символом ИВ.
Опр.
Формулы
![]() и
называются эквивалентными, если эту
эквивалентность можно вывести
и
называются эквивалентными, если эту
эквивалентность можно вывести
![]() .
.
Интерпретация формул
Формулы
ИВ можно интерпретировать (придать
смысл) как формулы АВ. Для этого свободные
переменные в ИВ нужно трактовать как
переменные АВ, принимающие значения (0
и 1). Конъюнкция, дизъюнкция, импликация
– связки, нужно определить как операции
АВ, следовательно, если при подстановке
в формулу
из ИВ вместо свободных переменных формул
![]() и
и
![]() ,
получается формула
или
,
то при такой же подстановке в формулу
рассматривается как формула из АВ
значения 0 и 1 она примет значение 0 или
1.
,
получается формула
или
,
то при такой же подстановке в формулу
рассматривается как формула из АВ
значения 0 и 1 она примет значение 0 или
1.
№58.Непротиворечивость исчисления высказываний.
Логическое исчисление называется непротиворечивым, если в нем нельзя вывести некоторую формулу и ее отрицание. В противном случае, исчисление называется противоречивым.
Такие исчисления никакой ценности не представляют, т.к. не могут отражать в себе различие между истиной и ложью.
Таким
образом, исчисление непротиворечиво,
если в нем для какой-либо формулы
нельзя вывести
и
![]() ,
пользуясь аксиомами и правилами вывода.
,
пользуясь аксиомами и правилами вывода.
Если ИВ противоречиво, то в нем выводима любая формула.
Если бы удалось показать, что существует какая-то невыводимая формула, то ИВ было бы непротиворечиво.
№59.Полнота исчисления высказываний.
Теорема. Всякая тождественно истинная формула алгебры высказываний выводима в исчислении высказываний.
He менее важное значение, чем понятие полноты в широком смысле, имеет понятие полноты логического исчисления в узком смысле.
Логическое исчисление называется полным в узком смысле, если присоединение к его аксиомам какой-нибудь не выводимой в нем формулы приводит к противоречию.
Исчисление высказываний полно также в узком смысле.
№60.Независимость аксиом и исчислений высказываний.
Аксиома, не выводимая из остальных аксиом, называется независимой от этих аксиом, а система аксиом, в которой ни одна аксиома не выводима из остальных, называется независимой системой аксиом. В противном случае система аксиом называется зависимой.
Вопрос о независимости одной аксиомы некоторой системы от других аксиом часто бывает равносилен вопросу о возможности заменить без противоречия в рассматриваемой системе данную аксиому ее отрицанием. В качестве примера можно указать вопрос о независимости пятого постулата Евклида в системе аксиом геометрии.
№61.Предикаты.
Предика́т— любое математическое высказывание, в котором есть, по меньшей мере, одна переменная. Предикат является основным объектом изучения логики первого порядка.
Неопределенные высказывания, или функции одной или нескольких переменных, называются логическими функциями или предикатами. Предикатом с одной переменной можно выразить свойство предмета, например: «х есть простое число», «х—прямоугольный треугольник»
№61.Кванторы.
Квантор всеобщности. Пусть R(x) - вполне определенный предикат, принимающий значение И или Л для каждого элемента х некоторой области M. Тогда выражение (x) R(х) - высказывание истинное, когда R(х) истинно для каждого элемента х области M, и ложное в противном случае. Это высказывание уже не зависит от х. Соответствующее ему словесное выражение будет: «для всякого х R(x) истинно». Символ (x) называется квантором всеобщности
Квантор существования.
Пусть R(х)
- некоторый предикат. Выражение (![]() x)
R(х)
–истинно, если существует элемент
области M,
для которого R(х)
истинно, и как ложь - в противном случае.
Знак
x
называется квантором существования.
x)
R(х)
–истинно, если существует элемент
области M,
для которого R(х)
истинно, и как ложь - в противном случае.
Знак
x
называется квантором существования.
№62.Аксиомы исчисления предикатов.
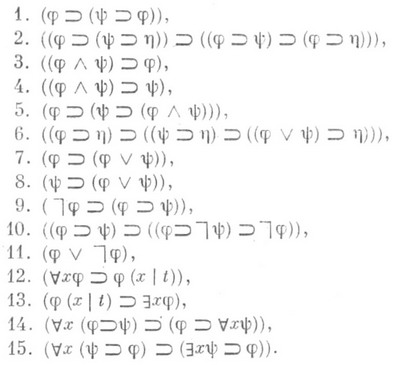
№64.Непротиворечивость и независимость аксиом.
Систему аксиом, для которой существует интерпретация, мы будем называть интерпретируемой или содержательно непротиворечивой. Систему аксиом, не допускающую никакой интерпретации, будем называть неинтерпретируемой или содержательно противоречивой. Независимость аксиом понимается в двух смыслах:
1) Аксиома называется независимой от остальных аксиом системы, если существует интерпретация остальных аксиом, не удовлетворяющая этой аксиоме.
2) Аксиома внутренне независима от остальных аксиом, если она не может быть выведена из остальных аксиом.
Аксиома зависима от остальных аксиом, если любая интерпретация этой системы удовлетворяет также и системе с аксиомой.