• Ориентированный граф

• Смешанный граф

• Изоморфные графы

№21.Основные понятия теории графов

Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины, прилегающие к одному и тому же ребру, называются смежными. Если ребра ориентированны, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом. Если ребра не имеют ориентации, граф называется неориентированным.

Путь в ориентированном графе — это последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей.

№22.Операции над Графами.

Объединение графов G₁ и G₂ , обозначаемое как , представляет такой граф , что множество его вершин является объединением Х₁ и Х₂ , а множество ребер – объединением A₁ и A₂

Пересечение графов G₁ и G₂ , обозначаемое как , представляет собой граф .

Кольцевая сумма двух графов G₁ и G₂ , обозначаемая как , представляет собой граф G₅ , порожденный на множестве ребер .

Удаление вершины. Если х_i -вершина графа G = (X, A), то G–х_i -порожденный подграф графа G на множестве вершин X–х_i , т. е. G–х_i является графом, получившимся после удаления из графа G вершины х_i и всех ребер, инцидентных этой вершине.

Удаление ребра или удаление дуги. Если a_i - дуга графа G = (X, A), то G-a_i – подграф графа G, получающийся после удаления из G дуги a_i .

Стягивание. Под стягиванием подразумевают операцию удаления дуги или ребра и отождествление его концевых вершин.

№23.Маршруты, цепи, циклы.

Маршрут в графе путь, ориентацией дуг которого можно пренебречь. Цепь маршрут, в котором все ребра попарно различны.

Пример (цепь). Маршрут a,{a,b},b,{b,c},c,{c,a},a,{a,d},d в первом графе из примера 1 является цепью, но не является простой цепью. Цикл замкнутый маршрут, являющийся цепью.

№24.Способы задания графов.

Графы могут задаваться следующими способами:

1. Геометрическим способом – рисунки, схемы, диаграммы,

2. Алгебраическим способом – перечислением вершин и ребер,

3. Табличным способом.

4. Матричным способом.

№25. Эйлеровы и Гамильтоновы графы.

Гамильтонов граф — граф, в котором есть гамильтонов цикл. Гамильтонов цикл — простой цикл в графе, содержащий все вершины графа ровно по одному разу

Эйлеров граф — это граф, в котором существует цикл, содержащий все рёбра графа по одному разу (вершины могут повторяться).

Эйлерова цепь (или Эйлеров цикл) — это цепь ( цикл), которая содержит все рёбра графа (вершины могут повторяться).

№26.Алгоритм поиска кратчайшего пути в графе. Алгоритм Дейкстры.

Алгоритм Дейкстры- Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании и технологиях, например, его использует протокол OSPF для устранения кольцевых маршрутов.

№27. Изоморфные Графы.

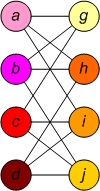
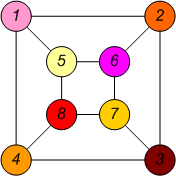
Изоморфизм. Два графа называются изоморфными, если существует перестановка вершин, при которой они совпадают. Иначе говоря, два графа называются изоморфными, если существует взаимно-однозначное соответствие между их вершинами и рёбрами, которое сохраняет смежность и инцидентность (графы отличаются только названиями своих вершин).

Граф G Граф H Изоморфизм между графами G и H Подстановка изоморфизма f

№28.Раскраска Графов. Хроматическое число.

Раскрашивать можно как ребра графа, так и вершины. Коснемся сначала задачи о раскраске вершин,. при этом считаем, что граф не ориентирован и не является мультиграфом.

Задача. Раскрасить вершины графа так, чтобы любые две смежные вершины были раскрашены в разные цветы, при этом число использованных цветов должно быть наименьшим. Это число называется хроматическим (цветным) числом графа, будем его обозначать =  (G) (если G – данный граф). Если число k , то граф называется k-раскрашиваемым.

Хроматическое число графа — минимальное количество цветов, требуемое для раскраски вершин графа, при которой любые вершины, соединенные ребром, раскрашены в разные цвета.

№29.Дать определение графа вида «дерево» и «лес»

Лес — неориентированный граф без циклов. Компонентами связности леса являются деревья. Дерево — связный граф, не содержащий циклов.

№30.Планарные и плоские Графы

Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер.

Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его вершины — это точки плоскости, а ребра — линии на ней. Области, на которые граф разбивает поверхность, называются гранями. Плоский граф — граф, уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу.

№31. Понятия о функции алгебры логики. Существенные и несущественные переменные.

Булева функция (функция алгебры логики) — функция, определённая на множестве упорядоченных наборов из нулей и единиц и принимающая на каждом из этих наборов значение 0 или 1.

Переменная x_i функции f (x₁, …, x_n) называется существенной, если существуют такие два набора из нулей и единиц, различающиеся только в i-й компоненте, что функция f на этих наборах принимает различные значения.

№32.Элементарные функции алгебры логики.

Двоичной, булевой функцией от набора двоичных переменных называется функция, результатом которой могут быть только значения 0 и 1. Любую булеву функцию можно задать с помощью таблицы, в которой всем возможным наборам значений двоичных переменных сопоставлены соответствующие им значения функции. Такая таблица называется таблицей истинности, поскольку она определяет истинность или ложность сложного высказывания в зависимости от истинности или ложности составляющих высказываний.

№33.Свойства логических функций.

1. Коммутативность

2. Идемпотентность

3. Ассоциативность

4. Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:

   • ,

   • ,

   • .

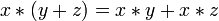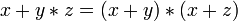5. Законы де Мо́ргана:

   • ,

   • .

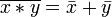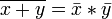6. Законы поглощения:

   • ,

   • .

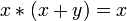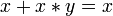№34.Реализайия функций формулами. Принцип двойственности.

Так же, как составные высказывания строятся из более простых, с помощью логических операций, можно комбинировать булевы переменные с помощью булевых опе­раций, получая булевы выражения, которые называются формулами.Всякой формуле однозначно соответствует некоторая функция, при этом говорят, что формула реализует функцию.

Принцип двойственности в абстрактной теории множеств. Пусть дано множество М. Рассмотрим систему всех его подмножеств А, В, С и т. д. Справедливо следующее предложение: если верна теорема о подмножествах множества М, которая формулируется лишь в терминах операций суммы, пересечения и дополнения, то верна также и теорема, получающаяся на данной путём замены операции суммы и пересечения соответственно операциями пересечения и суммы, пустого множества Λ — всем множеством М, а множества М — пустым множеством Λ.

№35.Разложение Булевых функций по переменным.

Рассмотрим вопрос представления n-местной булевой функции f(x₁,x₂,…,x_n) какой-нибудь формулой алгебры высказываний.

 

Введем обозначение , где - параметр, равный 0 или 1.

Очевидно, что

 

 

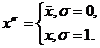
Теорема . Каждую функцию алгебры логики f(x₁,x₂,…,x_n) при любом m(1£m£n) можно представить в следующей форме:

(1),

 

где дизъюнкция берется по всевозможным наборам значений переменных .

№36. Совершенная Дизъюнктивная Нормальная Форма

СДНФ (Совершенная Дизъюнктивная Нормальная Форма) — это такая ДНФ, которая удовлетворяет трём условиям:

• в ней нет одинаковых элементарных конъюнкций

• в каждой конъюнкции нет одинаковых пропозициональных букв

• каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причем в одинаковом порядке.

№37. Совершенная Конъюнктивная Нормальная Форма

СКНФ (Совершенная Конъюнктивная Нормальная Форма) — это такая КНФ, которая удовлетворяет трём условиям:

• в ней нет одинаковых элементарных дизъюнкций

• в каждой дизъюнкции нет одинаковых пропозициональных букв

• каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.