8. Инвариантные подпространства. Собственные подпространства. Характеристическое уравнение. Свойства характеристическом многочлена. Приведение матрицы преобразования к диагональному виду.

Инвариантные подпространства: Подпространство L’ пространства L называется инвариантным относительно А, если для каждого вектора х из L’ образ A(x) лежит в L’.

Собственные подпространства: Нулевой вектор х, удовлетворяющий условию А(х)=λх, называется собственным вектором преобразования А. Число λ в этом равенстве называется собственным значением. Говорят, что собственный вектор х принадлежит собственному значению λ.

Характеристическое уравнение:

Свойства характеристическом многочлена: Если А и А’ – матрицы преобразования А в разных базисах, то характеристические многочлены этих матриц совпадают.

Пусть собственное значение λ₀ преобразования А является корнем характеристического уравнения кратности S. Тогда ему принадлежит не более s линейно независимых собственных векторов.

Приведение матрицы преобразования к диагональному виду: Квадратная матрица А с элементами αⁱ_j имеет диагональный вид или диагональная, если αⁱ_j=0 при i неравном j, т.е. могут быть отличны от нуля только элементы αⁱ_j , расположенные на главной диагонали.

Матрица линейного преобразования А в базисе e₁…e_n имеет диагональный вид тогда и только тогда, когда все векторы базиса – собственные векторы преобразования.

9. Евклидовы пространства. Скалярное произведение и его свойства. Неравенство Коши­-Буняковского и следствия из него. Ортонормированный базис. Скалярное произведение в произвольном и ортонормированном базисах. Матрица Грама.

Евклидовы пространства и свойства скалярного произведения: Вещественное линейное пространство называется евклидовым, если в нем определена операция скалярного умножения: любым двум векторам х и у сопоставлено вещественное число (обозначаемое (х.у)), и это соответствие удовлетворяет следующим условиям, каковы бы ни были векторы х,у, и z и число α: 1)(х,у)=(у,х) 2)(х+у,z)=(x,z)+(y,z) 3)(αx,y)= α(x,y) 4)(x,x)>0, если x неравен 0.

Простейшие следствия из аксиом: 1)(х,αу)=α(х,у) 2)(x. y+z)=(x,y)+(x,z) 3)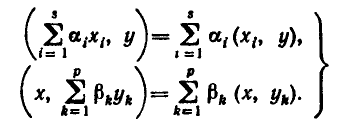 (1)

4) (x, 0) = 0

Неравенство Коши­-Буняковского и следствия из него: Пусть дано линейное пространство L со скалярным произведением (~,~). Пусть ||~|| - норма, порожденная скалярным произведением, то есть тогда для любых имеем , причем равенство достигается тогда и только тогда, когда векторы x и у пропорциональны (Коллинеарны).

Ортонормированный базис: Систему векторов f₁…f_m мы назовем ортонормированной, если (f_i,f_j)=0 при i неравном j и (f_i,f_i)=1 какими бы ни были i и j.

Ортонормированная система векторов линейно независима. В n-мерном евклидовом пространстве существует ортонормированная система из n-векторов.

Скалярное произведение в произвольном и ортонормированном базисах: Пусть в евклидовом пространстве задан базис е₁…е_n, тогда для произвольного базиса скалярное произведение примет вид:

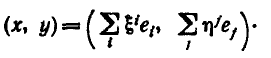Используя 1 формулу можем переписать в виде:

Для ортонормированного базиса:

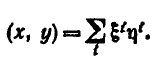
Матрица Грамма:

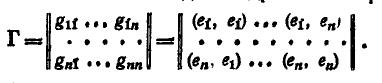
Эта матрица называется матрицей Грамма базиса e₁…e_n. Данная матрица не меняется при транспонировании, т.е. она симметричная