
Свойства Точка перегиба m обладает следующими свойствами:
в точке M кривая имеет единственную касательную,
в достаточно малой окрестности точки M кривая расположена внутри одной пары противоположных углов, образуемых касательной и нормалью.
Если слева и справа от критической точки x=x0 имеются такие промежутки (x0-δ, x0) и (x0, x0+δ) (где δ - некоторое положительное число), в каждом из которых f(x) сохраняет постоянный знак, то точка x=x0 будет точкой перегиба, если знаки f(x) в этих промежутках разные, и не будет ею, если знаки f(x) в этих промежутках одинаковые. Правило отыскания точек перегиба. 1). Находим вторую производную f(x) и определяем абсциссы точек, в которых f(x)=0 или не существует, например f(x)=∞. 2). Найденные точки исследуем при помощи достаточного признака наличия точки перегиба, определяя знаки f(x) слева и справа от каждой такой точки.
26. асимптоты кривой. необходимые и достаточные условия существования невертикальной асимптоты. Вертикальные асимптоты Асимптотой бесконечной ветки прямой наз-ся прямая, к каждой ветке неограниченно приближающаяся.прямая y=kx+b наз-ся асимптотой для кривой y=f(x), при х +∞ (или -∞) если lim [f(x)-kx-b]=0. Из данного определения следует, что кривая y=f(x) имеет невертикальную асимптоту у= b при х +∞ тогда и только тогда, когда lim f(x)=b. для существования асимптоты y=kx+b необходимо и достаточно, чтобы существовали конечные пределы lim f(x)/x=k (делили на х) и lim [f(x)-kx]=b. Находим точки х1, х2… вблизи которых функция неограниченно возрастает по обсолютной велечине (хотя бы с одной стороны от запланированной точки). Тогда прямые х=х1, х=х2… и будут вертикальными асимптотами.
функции нескольких переменных 1. определение функции двух (трех) переменных и ее области задания (определения). геометрическое истолкование этих понятий. функция от n переменных
V=XYZ – объем прямоугольного параллелепипеда (функции от 3х переменных).


 Пусть
D – Некоторое множество
пар (Х, Y) вещественных
чисел. На геометрическом языке D
представляет некое множество точек
плоскости oXY.
Пусть
D – Некоторое множество
пар (Х, Y) вещественных
чисел. На геометрическом языке D
представляет некое множество точек
плоскости oXY.
Определение: Переменная Z называется функцией от двух переменных X и Y, заданной на D, если каждой паре (X, Y) из D соответствует одно определенное значение переменной Z.
Переменные X и Y называются независимыми переменными или аргументами функции, множество D – областью задания или областью определения функции.
Обозначение: Z=f(X,Y), Z=ϕ(X,Y) и т.д.
Z
-
X0
Y0

Пример 1. В
силу закона Ома
 , где I – Сила тока, U
– Напряжение, R –
сопротивление в цепи.
, где I – Сила тока, U
– Напряжение, R –
сопротивление в цепи.
Тем самым I оказывается функцией от двух переменных U и R. Область задания характеризуется условием U≥0, R>0.
 Если
рассматривать множество oUR,
то область задания есть множество точек
(U, R),
заполняющих первую четверть (за
исключением точек оси oU).
Если
рассматривать множество oUR,
то область задания есть множество точек
(U, R),
заполняющих первую четверть (за
исключением точек оси oU).
Пример 2.
Найти область определения функции

 Решение:
Решение:
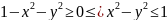 .
Область определения D
есть круг R=1 с центром 0,
включая его границу (т.е. окружность).
.
Область определения D
есть круг R=1 с центром 0,
включая его границу (т.е. окружность).
Функция
Z=f(X,
Y) геометрически
иллюстрируется следующим образом:
рассмотрим декартову систему координат
в пространстве (оXYZ) и
предположим область задания функции
│D│ представляет собой
некоторый один «кусок» плоскости oXY.
Возьмем некоторую точку P(X,
Y) D и вычислим соответствующее
значение Z.
D и вычислим соответствующее
значение Z.
P
M

Отрезок длиной │Z│ отложим на перпендикуляре к плоскости oXY, проходящей через точку P в ту или иную сторону, в зависимости от знака Z. В результате получим в пространстве точку M (X, Y, Z)
Тогда точка P перемещается в области задания D, соответственно точка M опишет в пространстве некоторую поверхность.
Эта поверхность служит геометрическим изображением функции z=f(x, y), служит, так сказать, ее «графиком».
 Например,
геометрическим изображением функции
(пример 2) служит верхняя полусфера сферы
радиуса 0 с центром в точке 0.
Например,
геометрическим изображением функции
(пример 2) служит верхняя полусфера сферы
радиуса 0 с центром в точке 0.

Определения понятий функции от трех и более переменных вводятся совершенно аналогично приведенному примеру.
Пусть, например, D – некоторое множество троек (X, Y, Z) вещественных чисел. На геометрическом языке D представляет собой какое-то множество точек пространства оХYZ.

Определение: Переменная “U” называется функцией от трех переменных X, Y, Z, заданной на Z, если каждой тройке из D соответствует одно определенное значение переменной “U”
И аналогично для функции от N переменных.
Обозначение: U=f(X, Y, Z) – функция трех переменных
V= ϕ(X, Y, Z, T) – функция четырех переменных
Y=F(x1, x2,…, xn) – функция от n переменных
Функцию F(x1, x2,…, xn) называют так же функцией точки n-мерного пространства и пишут f(P), подразумевая под P точку (x1, x2,…, xn)
Замечание: Уже функцию от трех переменных изобразить графически невозможно – отсутствует четвертая ось.
2* предел и непрерывность функции нескольких переменных
Тема: Предел и непрерывность нескольких переменных(на примере функции от двух переменных).
Понятие предела функции нескольких переменных вводится аналогично случаю функции одной переменной.
Раньше мы
использовали
 – окружность точки
– окружность точки
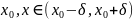
Пусть теперь
P0 (x0,
y0) – точки плоскости
oxy. Будем называть
r-окрестностью точку P0
(x0, y0)
совокупность всех точек P(x,y),
плоскости, расстояние которых от точки
P0 удовлетворяет
условию |P0P|<R
или, что то же самое
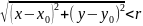
Иными словами, r-окружность точки P0 представляет собой открытый круг радиуса r с центром в P0.

Напомним некоторые понятия

Открытый круг состоит только из внутренних точек
Совокупность всех граничных точек называется его границей
Замкнутый круг состоит из внутренних и граничных точек.
Пусть функция z=f(x, y) задана в некоторой области D плоскости oxy. Рассмотрим некоторую определенную точку P0 (x0, y0), множества в области D.
Определение:
Число А называется пределом функции
f(x,y)
в точке P0 (x0,
y0), если для любого
числа
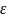 >0
существует такое число r>
>0
существует такое число r>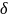 ,
что для всех точек P(x,y)
выполняется неравенство
,
что для всех точек P(x,y)
выполняется неравенство
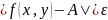
Обозначение:
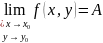 или
или
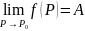
Основные теоремы теории пределов функции одной переменной переносятся и на случай функции нескольких переменных
Пример 1.
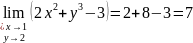
Пример 2.
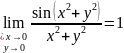
Определение 2. Пусть точка P0 (x0, y0) принадлежит области задания функции z=f(x,y). Функция f(x,y) называется непрерывной в точке P0 (x0, y0), если имеет место равенство
 (1)
(1)
Условию (1) непрерывность функции можно предать равносильную и весьма употребительную форму.
Прежде всего равенство (1) эквивалентно такому:
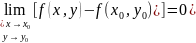 (1’)
(1’)
Если ввести
обозначение
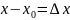 ,
,
 ,
,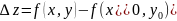 или,
что то же самое, положить
или,
что то же самое, положить
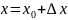 ,
y
,
y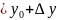 ,
,
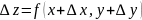 ,
то равенство (1’) запишем так:
,
то равенство (1’) запишем так:
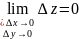 (2)
(2)
Величины
и
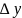 называются приращениями независимых
переменных,
называются приращениями независимых
переменных,
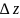 – приращением функции.
– приращением функции.
Итак, функция
z=f(x,y)
непрерывна в точке
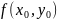 ,
когда выполнено равенство (1’), т.е.
приращение функции стремится к нулю,
когда стремятся к нулю приращения
независимых переменных.
,
когда выполнено равенство (1’), т.е.
приращение функции стремится к нулю,
когда стремятся к нулю приращения
независимых переменных.
Замечание. Равенство (2) можно записать так:
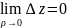 ,
где
,
где
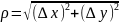
Величина
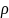 ,
очевидно, представляет собой расстояние
между исходной точкой
,
очевидно, представляет собой расстояние
между исходной точкой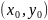 и «сдвинутой» точкой (
и «сдвинутой» точкой (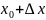 ,
,
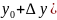 .
.

Функцию, непрерывную в каждой точке некоторой области называют непрерывной в этой области.
Если функция
f(x,y)
не является непрерывной в точке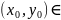 области задания функции, то говорят,
что функция терпит разрыв в этой точке,
а саму точку
называют точкой разрыва функции.
области задания функции, то говорят,
что функция терпит разрыв в этой точке,
а саму точку
называют точкой разрыва функции.
Условимся относить к точке разрыва те точки, которые не принадлежат области задания функции, но являются граничными точками этой области.
Пример 1.
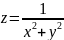
Область задания – вся плоскость оxy, если удалить из нее точку 0(0,0). Соответствующая поверхность имеет вид:

Функция непрерывна в каждой точки задания область т.к.
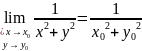 ,
если
,
если
 соответственно не равны нулю.
соответственно не равны нулю.
Точка (0,0) является, очевидно, граничной точкой области задания и, в соответствии с нашей договоренностью будет точкой разрыва.
3. частные производные: определение, геометрический смысл. частные производные высших порядков
Тема. Частные производные и частные дифференциалы.
Рассмотрим функцию z=f(x,y) (1) и точку из области задания этой функции

Станем
изменять x, оставляя
значение y=y0
постоянным. В результате получим функцию
 из одной переменной x.
из одной переменной x.
Если эта функция имеет производную (по х) при y=y0, то последнюю называют частным производным от функции z=f(x,y) по х в точке и обозначают одним из символов:
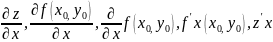
Замечание:
Символы
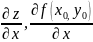 всегда цельные, нераздельные, как дроби
их трактовать нельзя. Символ
всегда цельные, нераздельные, как дроби
их трактовать нельзя. Символ
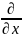 так же цельный – это символ операции.
так же цельный – это символ операции.
Положим
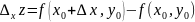 и назовем эту величину частным приращением
функции z по x
в точке
и назовем эту величину частным приращением
функции z по x
в точке
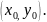 Тогда по смыслу данного нами определения
Тогда по смыслу данного нами определения
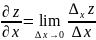 (2)
(2)
Аналогично,
если функция f(x0,
y) от одной переменной y
(y меняется,
 )
имеет производную (по y)
при y=y0,
то эту производную называют частным
производным от функции z=f(x,y)
по y в точке
)
имеет производную (по y)
при y=y0,
то эту производную называют частным
производным от функции z=f(x,y)
по y в точке и
обозначают одним из символов:
и
обозначают одним из символов:
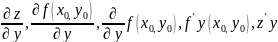
И здесь по смыслу определения
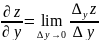 где
где
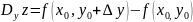 – частное приращение функции z
по y в точке
.
– частное приращение функции z
по y в точке
.
Практически
частные производные находят по известным
правилам дифференцирования функции
одной переменной: при нахождении
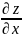 необходимо y считать
постоянной, при нахождении
необходимо y считать
постоянной, при нахождении
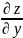 необходимо x считать
постоянной.
необходимо x считать
постоянной.
Пример 1.
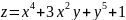
В любой точке (x,y) плоскости oxy
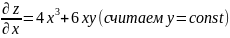
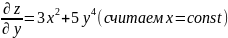
Пример 2.
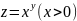
В любой точке (x,y) лежащей правее оси oy:
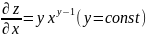
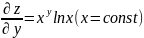
Геометрический смысл частных производных второго порядка.
Вспомним: значение в точке получалось дифференцированием по x функции f(x, y0). Но эта функция представляет собой переменную аппликатуру кривой Fx, получаемой в сечении поверхности z=f(x,y) плоскостью y=y0 (параллельной плоскости oxz).
Кривая Fx может рассматриваться как график функции f(x, y0) (В плоскости y=y0).

Отсюда следует, что есть тангенс угла α, образованного касательной к линии Fx и осью ox, т.е.
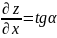 ,
аналогично
,
аналогично
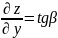 (3)
(3)
Частными дифференциалами функции z по x и y в точке (x0, y0) называются величины
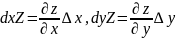 (4)
(4)
Назовем
(подобно случаю одной переменной)
дифференциалами независимых переменных
их приращения т.е. получим
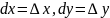
Тогда формулы (3) примут вид
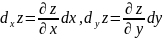 (5)
(5)
Для функции
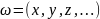 (6) от любого числа переменных частные
производные и дифференциалы выводятся
аналогично случаю функции двух переменных.
(6) от любого числа переменных частные
производные и дифференциалы выводятся
аналогично случаю функции двух переменных.
Частные
производные от функции
 по каждой из переменных есть обычная
производная по этой переменной той
функции, которую получают, когда всем
другим переменных дают постоянные
значения. Символика остается прежней.
При этом, если речь идет о точке (x0,
y0, z0),
то
по каждой из переменных есть обычная
производная по этой переменной той
функции, которую получают, когда всем
другим переменных дают постоянные
значения. Символика остается прежней.
При этом, если речь идет о точке (x0,
y0, z0),
то
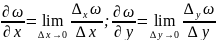 и т.д. где положено
и т.д. где положено
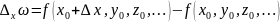 и т.д. – частные приращения функции (6)
по x,…. и т.д.
и т.д. – частные приращения функции (6)
по x,…. и т.д.
Пример.
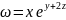
В любой точке
( x,y,z)
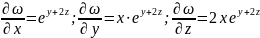
Частный
дифференциал функции
 по какой-либо из переменных есть
произведение соответствующей частной
производной на дифференциал этой
переменной.
по какой-либо из переменных есть
произведение соответствующей частной
производной на дифференциал этой
переменной.
 и т.д.
и т.д.
Тема. Частные производные высших порядков
Пока речь у нас шла о частных производных первого порядка или, короче, первых частных производных. Но первые частные производные сами являются функциями от нескольких переменных и, в свою очередь, могут иметь частные производные.
Последние производные по отношению к исходной функции будут частными производными второго порядка. При этом используются следующие обозначения (для простоты говорим о функции z=f(x,y) от двух переменных)
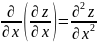 (или
(или
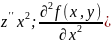 –
первое и второе дифференцирование по
x
–
первое и второе дифференцирование по
x
 (или
(или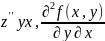 )
– первое дифференцирование по y
второе по x
)
– первое дифференцирование по y
второе по x
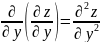 (или
(или
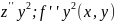 )
– первое и второе дифференцирование
по y
)
– первое и второе дифференцирование
по y
Пример.
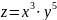
В любой точке (x,y)
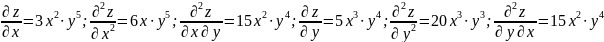
Замечаем,
что
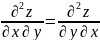
Частные производные третьего, четвертого и прочих порядков вводятся совершенно аналогично:
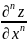 – функция дифференцируется по x
– функция дифференцируется по x
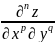 где
p+q=n
– функция дифференцируется p
раз по x, а затем q
раз по y и т.д.
где
p+q=n
– функция дифференцируется p
раз по x, а затем q
раз по y и т.д.
Частные производные второго, третьего или большего порядка являются результатом дифференцирования по разным переменным, называется смешанной.
Смешанными
будут, например, производные

Теорема.
Пусть в некоторой окрестности точки
функция z=f(x,y)
имеет смешанные частные производные
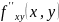 и
и
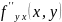 и эти производные непрерывны в точке
,
тогда
и эти производные непрерывны в точке
,
тогда
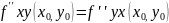 (Без доказательства)
(Без доказательства)
Следствие. Если вторые смешанные производные непрерывны в каждой точке некоторой открытой области, то они совпадают в каждой точке этой области.
Замечание. Сформулированная теорема обобщается на случай смешанных производных любого порядка и на функции любого числа переменных.
4. дифференцируемость функции нескольких переменных. полный дифференциал первого порядка
Тема. Дифференцируемость функции нескольких переменных. Полный дифференциал первого порядка.
Рассмотрим
функцию z=f(x,y)
(1) от двух переменных и точку (x,y)
из области задания функции. Величину
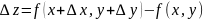 (2), где
и
такие приращения независимых переменных,
что точка
(2), где
и
такие приращения независимых переменных,
что точка
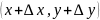 принадлежит области задания функции,
называют полным приращением функции
(1) в точке
принадлежит области задания функции,
называют полным приращением функции
(1) в точке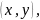 в отличие от частных приращений,
рассмотренных ранее.
в отличие от частных приращений,
рассмотренных ранее.
Определение 1. Функция (1) называется дифференцируемой в точке (x,y), если выполнены следующие два условия:
1. В этой точке
существуют конечные частные производные
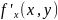 и
и

2. Полное приращение функции (1) в точке (x,y) представлено в виде:
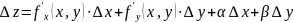 (3)
(3)
где
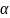 и
и
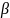 стремятся к нулю при
стремятся к нулю при
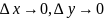 или, что то же самое, при
или, что то же самое, при
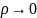 ,
где
,
где
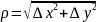 –
расстояние между исходной точкой
–
расстояние между исходной точкой
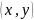 и «сдвинутой» точкой
и «сдвинутой» точкой

Замечание 1. Из выполнения условия (1), т.е. из наличия конечных частных производных не всегда вытекает справедливость условия (2). Иными словами функция может иметь конечные частные производные и при этом не быть дифференцируемой. Здесь мы видим что существует различие между функцией одной и нескольких переменных, поскольку там дифференцировать функции и наличие конечной производной означают одно и то же. Замечание 2. Нетрудно показать, что равенству (3) можно придать следующую форму:
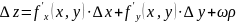 (3’)
(3’)
Определение 2. Если функция (1) дифференцируема в точке (x,y), то ее полным дифференциалом первого порядка в этой точке называют величину
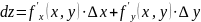 (4)
(4)
Т.к. для
независимых переменных мы условились
считать, что
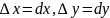 ,
то равенство (4) можно переписать так:
,
то равенство (4) можно переписать так:
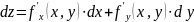 (5)
(5)
Или так:
 (5’)
(5’)
Полный дифференциал, как мы видим, оказался равен сумме частных дифференциалов
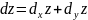 (6)
(6)
Сопоставив формулы (4) и (3) ( или 3’), можно прийти к выводу, что полный дифференциал:
1. Меняется относительно и
2. Отличается от полного приращения на величину бесконечно малую более высокого порядка малости, чем

Этим широко пользуются в приближенных вычислениях, заменяя приращение функции более простым по структуре ее дифференциалом
Теорема 1. Если функция z=f(x,y) дифференцируема в точке (x,y), то она непрерывна в этой точке
Действительно, из равенства (3) сразу следует, что , а это и означает непрерывность функции (1) в точке (x,y)
Замечание.
Обратная теорема в общем случае неверна.
Например, функция
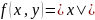 непрерывна в каждой точке плоскости
oxy, но не дифференцируема
в каждой точке оси оy. Хотя
бы по той причине, что
непрерывна в каждой точке плоскости
oxy, но не дифференцируема
в каждой точке оси оy. Хотя
бы по той причине, что
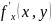 не существует при x=0
не существует при x=0

Теорема 2. (признак дифференцируемости функции)
Если в
некоторой окрестности точки
функция z=f(x,y)
имеет первые частные производные
,
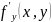 ,
которые непрерывны в самой точке
,
f(x,y)
дифференцируема в этой точке. (Без
доказательства).
,
которые непрерывны в самой точке
,
f(x,y)
дифференцируема в этой точке. (Без
доказательства).
Пример.
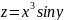
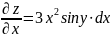 ;
;
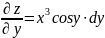
Эти частные производные всюду непрерывны, функция всюду дифференцируема и по формуле (5’):
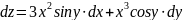
Функцию, дифференцируемую в каждой точке некоторой области, называют дифференцируемой в этой области.
Понятие. Дифференцируемость функции от трех и большего числа переменных вводится аналогично случаю функции двух переменных.
5. касательная плоскость и нормаль к поверхности
Тема. Касательная плоскость и нормаль к поверхности
 Пусть
M – фиксированная точка
на данной поверхности. Рассмотрим на
поверхности другую переменную точку
M’ и проведем секущую
MM’.
Пусть
M – фиксированная точка
на данной поверхности. Рассмотрим на
поверхности другую переменную точку
M’ и проведем секущую
MM’.
Определение
1.Плоскость
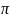 ,
проходящая через точку M,
называется касательной плоскостью к
поверхности в этой точке, если угол
между секущей MM’ и этой
плоскостью стремится к нулю, когда
расстояние |MM’| стремится
к нулю, по какому бы закону точка M’,
оставаясь на поверхности, не приближалась
к M.
,
проходящая через точку M,
называется касательной плоскостью к
поверхности в этой точке, если угол
между секущей MM’ и этой
плоскостью стремится к нулю, когда
расстояние |MM’| стремится
к нулю, по какому бы закону точка M’,
оставаясь на поверхности, не приближалась
к M.
Определение 2. Нормалью к поверхности в точке M называется прямая, проходящая через точку M перпендикулярно к касательной плоскости.
Отметим, что не всякая поверхность в каждой точке обязательно имеет касательную плоскость, а следовательно, и нормаль. Так, например, круглый конус в его вершине лишен касательной плоскости (в смысле высказанного определения).
Рассмотрим теперь поверхность заданную уравнением вида: z=f(x,y) (1)и предположим, что функция (1) дифференцируема в точке . Последнее означает, что:
(2)
Где
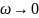 при
,
или, в других обозначениях:
при
,
или, в других обозначениях:
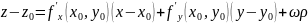 (3)
(3)
Оказывается,
если в равенстве (3) пренебречь членом
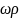 бесконечно малым более высокого порядка
малости, чем
,
то мы получим уравнение касательной
плоскости к поверхности (1) в точке
бесконечно малым более высокого порядка
малости, чем
,
то мы получим уравнение касательной
плоскости к поверхности (1) в точке
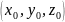 ,
где
,
где
 .
Т.е. справедлива следующая теорема:
.
Т.е. справедлива следующая теорема:
Теорема. Если
функция f(x,y) дифференцируема в точке
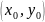 ,
то поверхность (1) в соответствующей
точке
заведомо имеет касательную плоскость,
уравнение которой имеет вид:
,
то поверхность (1) в соответствующей
точке
заведомо имеет касательную плоскость,
уравнение которой имеет вид:
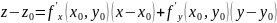 (4) (Без доказательства)
(4) (Без доказательства)
Замечание. Уравнение (4) имеет вид, показывающий, что в нашем случает касательная плоскость не перпендикулярна плоскости oxy. Зная уравнение касательной плоскости, легко написать уравнение нормали. Запишем уравнение (4) в таком виде:
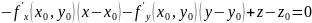 (5)
(5)
Тогда
={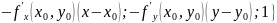 – нормальный вектор касательной
плоскости. Прямую в пространстве можно
задать так:
– нормальный вектор касательной
плоскости. Прямую в пространстве можно
задать так:
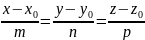 ,
где
,
где
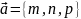 – направленный вектор прямой.
– направленный вектор прямой.
В силу условия перпендикулярности прямой и плоскости
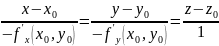 – уравнение нормали к заданной поверхности
в точке M
– уравнение нормали к заданной поверхности
в точке M
Пример.
Написать уравнения касательной плоскости
к поверхности
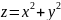 в точке M(1,2,6)
в точке M(1,2,6)
 Данная
поверхность – парабола вращения.
Данная
поверхность – парабола вращения.
Находим
 ,
,
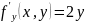 .
Эти частные производные всюду непрерывны,
следовательно, функция всюду дифференцируема
и касательная плоскость в точке M
заведомо существует.
.
Эти частные производные всюду непрерывны,
следовательно, функция всюду дифференцируема
и касательная плоскость в точке M
заведомо существует.
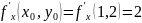 ;
;
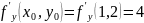
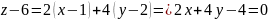 – уравнение касательной плоскости
– уравнение касательной плоскости
Уравнение
нормали:
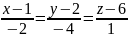
6* дифференцирование сложных и неявных функций
Тема. Производные и дифференциалы сложной функции
Рассмотрим функцию z=f(u,v) (1) от двух переменных u,v, дифференцируемую в каждой точке открытой области D
Положим
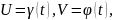 где t изменяется в некотором
промежутке, причем не выходит из области
D. В результате z
станет сложной функцией от одной
переменной t. Полагаем
что если функции
где t изменяется в некотором
промежутке, причем не выходит из области
D. В результате z
станет сложной функцией от одной
переменной t. Полагаем
что если функции
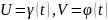 дифференцируемы по t и
тогда:
дифференцируемы по t и
тогда:
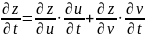 (2)
(2)
Действительно,
пусть
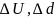 – приращения переменных U
и V, вызванные приращением
– приращения переменных U
и V, вызванные приращением
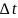 .
Т.к. функция (1) дифференцируема, то для
этих
.
Т.к. функция (1) дифференцируема, то для
этих
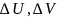 имеет место равенство
имеет место равенство
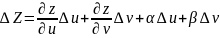 (3)
(3)
Где
 при
при
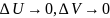
Но функции
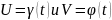 дифференцируемы и, следовательно,
непрерывны, т.е.
при
дифференцируемы и, следовательно,
непрерывны, т.е.
при
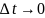
Перепишем равенство (3) в виде:

Если перейдем
здесь к пределу при
,
то убедимся в существовании производной
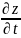 и справедливости равенства (2).
и справедливости равенства (2).
Замечание 1. Формула (1) легко воспроизводится, если использовать следующую схему:

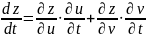
 Замечание
2. Если
Замечание
2. Если
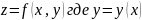 ,
то по схеме и по формуле (2) (u=x,
v=y, t=x)
получаем
,
то по схеме и по формуле (2) (u=x,
v=y, t=x)
получаем
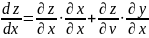 и т.к.
и т.к.
 то
то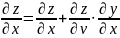 (4)
(4)
Формула (4)
носит название формулы для вычисления
полной производной
 (в отличии от частного производного
)
(в отличии от частного производного
)
Пример.
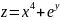 ,
где
,
где
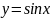
Найти
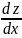
Решение.
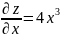 ,
,
 ,
непрерывны при всех x,y.
Следовательно, функция z
дифференцируема на всей плоскости и по
формуле (4) находим
,
непрерывны при всех x,y.
Следовательно, функция z
дифференцируема на всей плоскости и по
формуле (4) находим
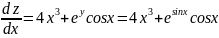
Обратимся
вновь к равенству (2). Умножив обе части
этого равенства на dt
получим
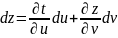 (5)
(5)
Формула (5)
показывает, что дифференциал сложной
функции
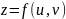 ,
где
выражается через u, v,
du, dv точно
так же как если бы U и V
были бы независимыми переменными.
,
где
выражается через u, v,
du, dv точно
так же как если бы U и V
были бы независимыми переменными.
Таким образом, как и в случае функции одной переменной мы имеем инвариантность формы дифференциала.
Если
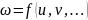 - функция от
- функция от
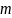 переменных,
функции от
переменных,
функции от
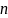 переменных, то при выполнении
соответствующих условий существуют
частные производные
переменных, то при выполнении
соответствующих условий существуют
частные производные

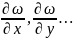 и эти производные находятся по формулам,
аналогично формуле (2)
и эти производные находятся по формулам,
аналогично формуле (2)
Пусть,
например,
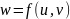 ,
где
,
где
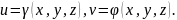 Тогда
по схеме
Тогда
по схеме
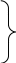
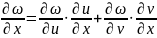
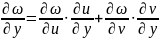 (6)
(6)
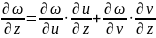
Тема. Дифференцирование неявно заданных функций.
Рассмотрим
уравнение
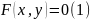 и пусть функция
и пусть функция
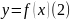 неявно задана этим уравнением.
неявно задана этим уравнением.
Допустим, что :
1.
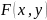 – дифференцируема в интересующей нас
области oxy;
– дифференцируема в интересующей нас
области oxy;
2. Функция дифференцируема по Х
Посчитаем теперь функцию (2) подставленной в уравнение (1). Тогда левая часть этого уравнения обратится в сложную функцию от х, постоянно равную нулю(т.е. постоянная величина)
Следовательно, производная от этой сложной функции так же будет равной нулю, и мы, в соответствии с правилом дифференцирования сложной функции, получим
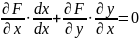 или
или
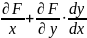 ;
Отсюда
;
Отсюда
 (4)
(4)
при единственном
дополнительном условии, что для
соответствующей точки
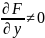 (5)
(5)
Вывод: при
выполнении условий (1) (2) и (5) мы можем
вычислить
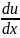 для функции (2) даже не зная фактически
этой функции, а зная лишь точку х, в
которой вычисляется производная и
соответствующее значение y.
для функции (2) даже не зная фактически
этой функции, а зная лишь точку х, в
которой вычисляется производная и
соответствующее значение y.
Пример.
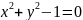 (6)
(6)
Это уравнение окружности с центром в точке 0

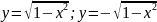 (7)
(7)
В нашем случае частные производные:
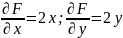 непрерывны при всех
непрерывны при всех
 .
Следовательно, функция
дифференцируема
на всей плоскости
.
Следовательно, функция
дифференцируема
на всей плоскости
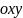 и по формуле (4) находим для каждой из
функций (7)
и по формуле (4) находим для каждой из
функций (7)
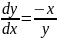 (всюду, где
(всюду, где
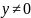 ,
т.е. кроме точек (-1,0) и (1,0)).
,
т.е. кроме точек (-1,0) и (1,0)).
Рассмотрим
теперь уравнение
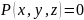 (8) и пусть функция
(8) и пусть функция
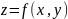 (9)неявно задана этим уравнением
(9)неявно задана этим уравнением
Предположим, что:
1.
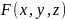 дифференцируема (как функция трех
переменных) в интересующей нас области
oxy
дифференцируема (как функция трех
переменных) в интересующей нас области
oxy
2. Функция (9) дифференцируема по x,y
Будем считать функцию (9) подставленной в уравнение (8). Тогда левая часть этого уравнения обратится в сложную функцию от x и y. Тогда и частные производные от этой сложной функции по x и y так же будут равны нулю, и мы в соответствии с правилом дифференцирования сложной функции получим:
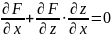
(10)
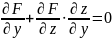
Аналогичным образом находятся частные производные неявных функций от любого числа переменных.
Тема. Полные дифференциалы высших порядков.
Функция от нескольких переменных называется n раз дифференцированной, если дифференцирована она сама и все ее частные производные до (n-1) порядка включительно.
Рассмотрим функцию (1) где x и y независимые переменные (а не функции от каких-либо других переменных). Если функция z дифференцируема, то ее полный дифференциал 1-го порядка имеет вид
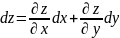 (2),
(2),
При чем, здесь – производные приращения независимых переменных, т.е. производные числа никак не зависящие от x и y
Поэтому мы
можем изменять x и y,
оставляя
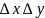 постоянными. Тогда
постоянными. Тогда
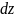 станет функцией от двух переменных:
x,y. Если при
этом функция (1) дифференцируема 2 раза,
то
будет дифференцируемой функцией (см.
(2)), и мы полагаем, что
станет функцией от двух переменных:
x,y. Если при
этом функция (1) дифференцируема 2 раза,
то
будет дифференцируемой функцией (см.
(2)), и мы полагаем, что
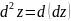
Величина
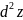 называется
полным дифференциалом второго порядка
функции z и, в свою очередь,
является функцией от x и
y, при чем выражается через
вторую частную производную функции z.
называется
полным дифференциалом второго порядка
функции z и, в свою очередь,
является функцией от x и
y, при чем выражается через
вторую частную производную функции z.
Вообще, если
функция (1) дифференцируема n
раз, то ее последний дифференциал n-го
порядка определяется равенством:
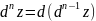 .
При этом помним, что независимые
переменные считаем постоянными.
.
При этом помним, что независимые
переменные считаем постоянными.
Найдем явное
выражение для
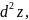 по
смыслу определения и в силу равенства
(2).
по
смыслу определения и в силу равенства
(2).
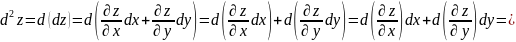
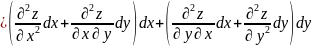
Можно показать, что в наших условиях . Поэтому
 (3)
(3)
7. экстремумы функций нескольких переменных
Тема. Экстремум функции нескольких переменных.
Пусть функция
задана в области D,
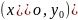 – внутренняя точка этой области. Говорят,
что функция
– внутренняя точка этой области. Говорят,
что функция
 имеет в точке
максимум, если всюду в некоторой
окрестности этой точки, за исключением
самой точки
,
выполняется неравенство:
имеет в точке
максимум, если всюду в некоторой
окрестности этой точки, за исключением
самой точки
,
выполняется неравенство:
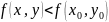 (1)
(1)
Говорят, что функция имеет в точке минимум, если всюду в некоторой окрестности этой точки, за исключением самой точки , выполняется следующее неравенство:
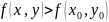 (2)
(2)
Понятия
максимум и минимум имеют локальный
характер, поскольку в определении
фигурирует лишь
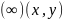 ,
достаточно близких к
,
достаточно близких к

Функция может иметь несколько максимумов и минимумов как и в случае одной переменной, вместо отдельных терминов «максимум» и «минимум» используют термин «экстремумы».
Теорема 1.
Пусть функция
имеет в точке
экстремум. Если при этом
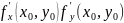 существуют и конечны, то
существуют и конечны, то
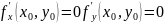 (3)
(3)
Если имеет
место максимум, то справедливо неравенство
(1). В частности,
 для всех x, достаточно
близких к
для всех x, достаточно
близких к
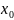 .
Т.е. имеет максимум в точке
.
Т.е. имеет максимум в точке
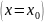 функция одной переменной
функция одной переменной
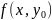 .
.
Отсюда следует (1) из равенства (3). Второе равенство доказывается аналогично.
Следствие
1. Если функция
имеет в точке
экстремум и дифференцируема в этой
точке, то ее полный дифференциал n-го
порядка обращается в этой точке в нуль.
Т.е.
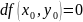
Теорема 2.
Пусть
Если при этом последний дифференциал
второго порядка
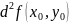 сохраняет
знак (не обращаясь в нуль) при
сохраняет
знак (не обращаясь в нуль) при
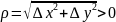 ,
то в точке
экстремум имеется, причем, в случае
,
то в точке
экстремум имеется, причем, в случае
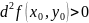 –
минимум, а в случае
–
минимум, а в случае
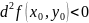 – максимум. Если же
– максимум. Если же
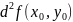 меняет знак, то экстремума в точке
нет. (Без доказательства).
меняет знак, то экстремума в точке
нет. (Без доказательства).
Тема. Отыскание наибольших и наименьших значений функции.
Имеет место теорема (аналог теоремы Вейштрасса)
Теорема. Если
функция
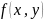 непрерывна в ограниченной замкнутой
области D, то она принимает
в этой области как свое наибольшее, так
и свое наименьшее значение.
непрерывна в ограниченной замкнутой
области D, то она принимает
в этой области как свое наибольшее, так
и свое наименьшее значение.
Для отыскания этих значений сначала находятся критические точки, лежащие внутри области D, вычисляются значения функции в этих точках и сравниваются со значениями функции на границе области.
Наибольшее (соответственно наименьшее) и будет наибольшим (наименьшим) значением функции в области D.
Замечание. Если область D не является замкнутой и ограниченной, то среди значений функции может не быть ни наибольших, ни наименьших.
