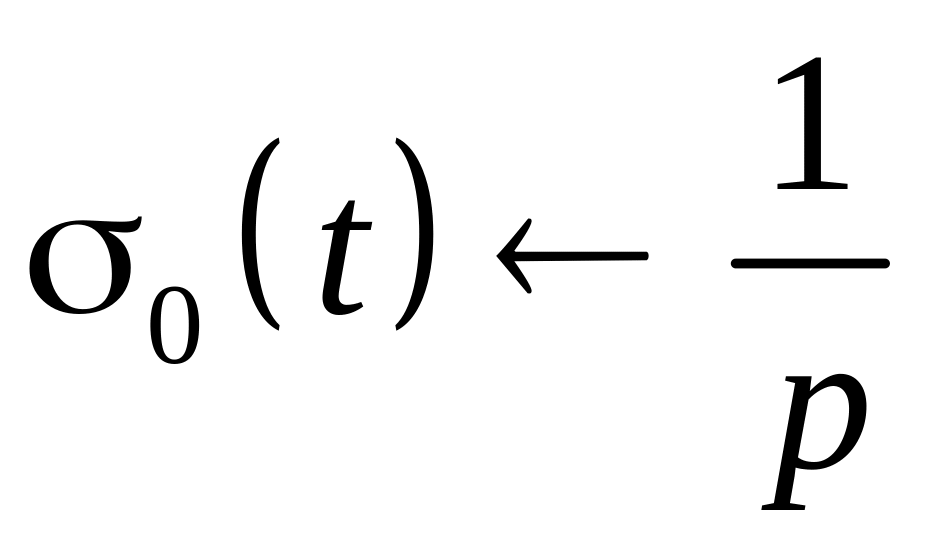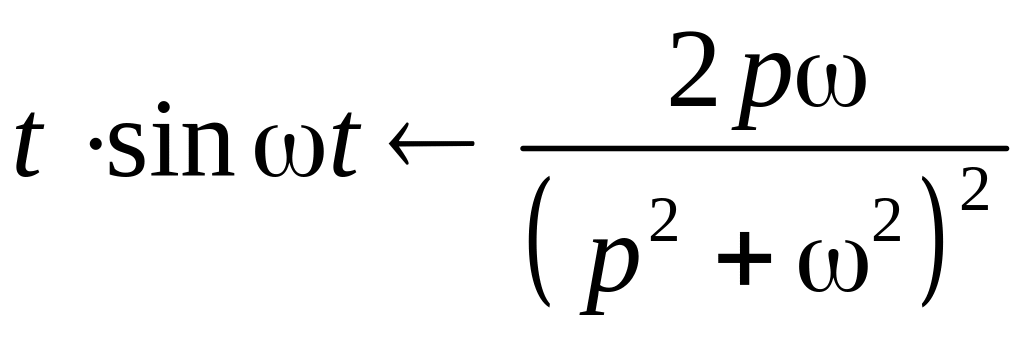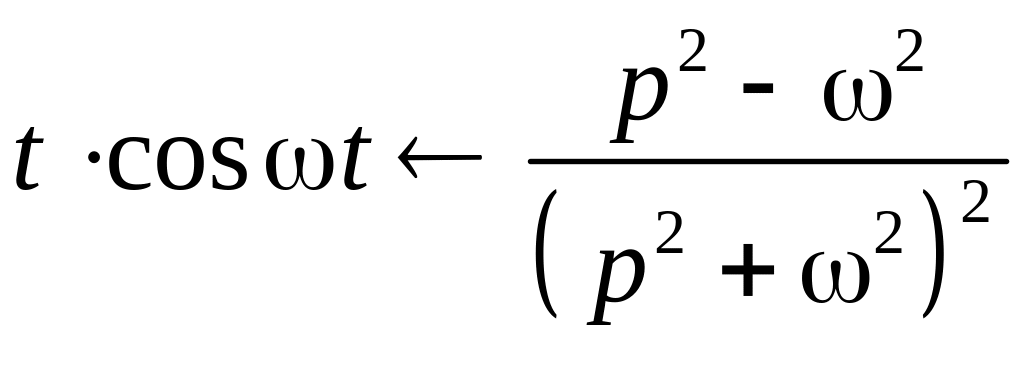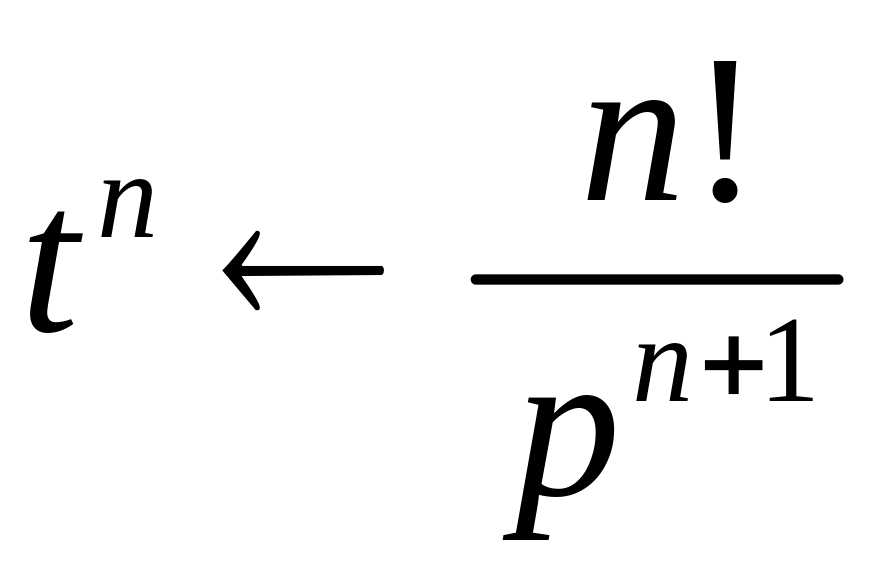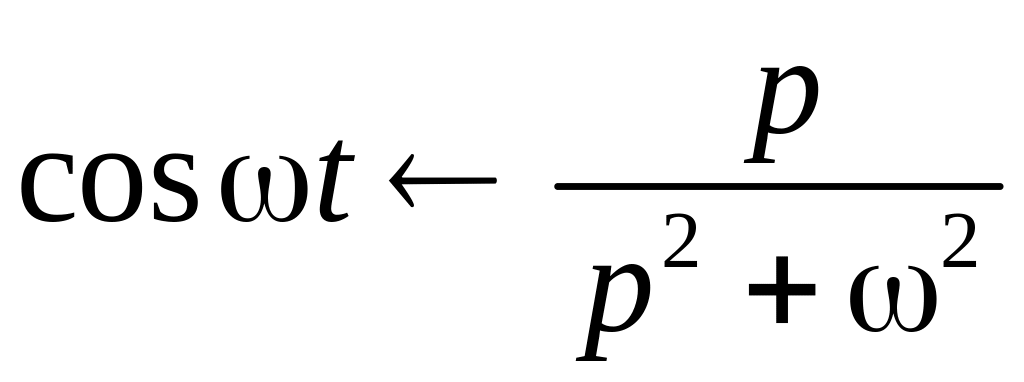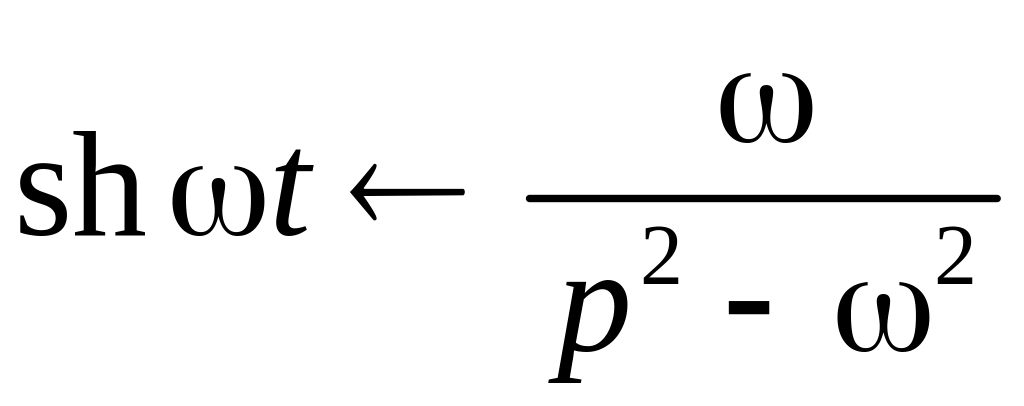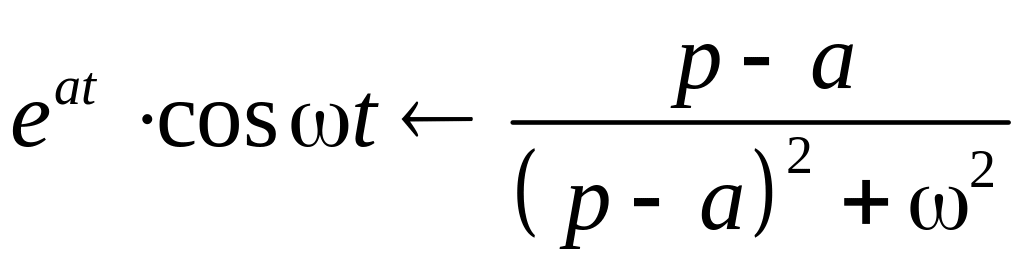Примеры нахождения изображений

1. Рассмотрим функцию . Функция называется единичной функцией Хевисайда.

   1 0 t

   . Итак, , причем функция определена в области .

2. Рассмотрим функцию 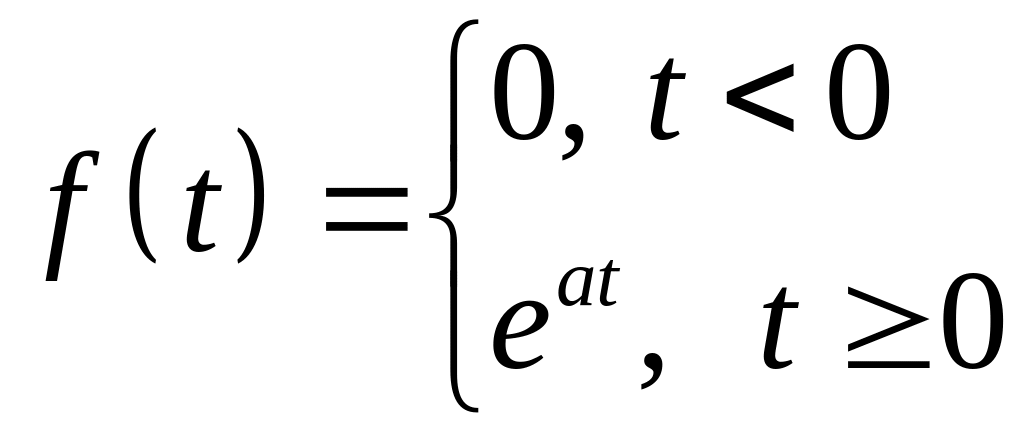, где а – комплексное число.

Имеем: 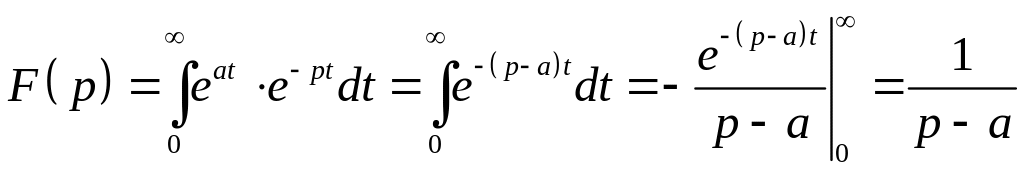, если или (т.е. правее прямой ).

Итак .

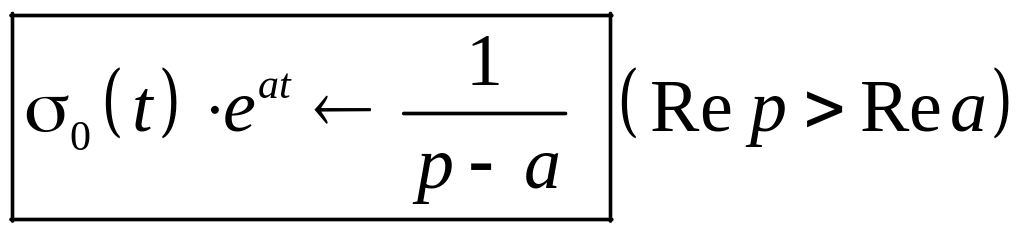Роль множителя в левой части состоит в том, что он «гасит» (обращает в нуль) функцию при . В дальнейшем будем считать, что все рассматриваемые нами функции снабжены множителем , хотя сам этот множитель в написании часто будем опускать.

3. Рассмотрим функцию .

Имеем: 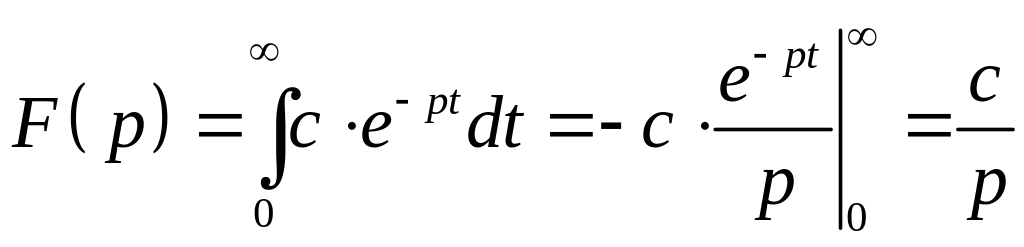. Итак, .

Вопрос 2. Простейшие свойства преобразования Лапласа.

Теорема (о единственности изображения).

Если две непрерывные функции и имеют одно и то же изображение, то эти функции тождественно равны: .

Теорема (о линейности изображения).

Изображение суммы нескольких функций, умноженных на постоянные, равно сумме изображений этих функций, умноженных на соответствующие постоянные, т.е. если

,

где – произвольные комплексные числа и для , а , то

.

Или, .

Доказательство.

Справедливость теоремы вытекает из свойства линейности интеграла, определяющего изображение.

Умножим обе части равенства на , получим

.

Вычислим несобственный интеграл в пределах от 0 до :

, что и т.д.

На основании этого свойства, получаем

,

таким образом .

Аналогично находим, что .

Рассмотрим гиперболическую функцию

,

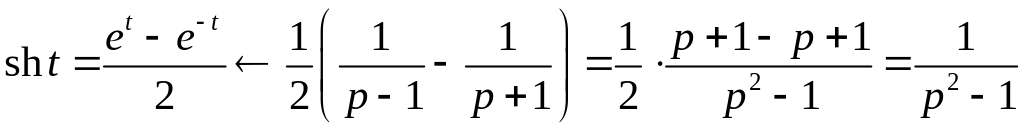таким образом, .

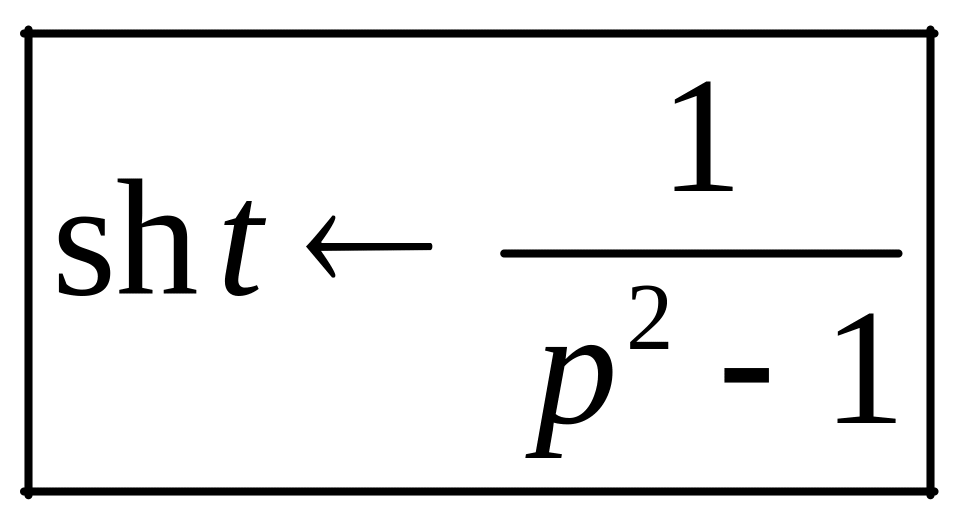Аналогично находим, что .

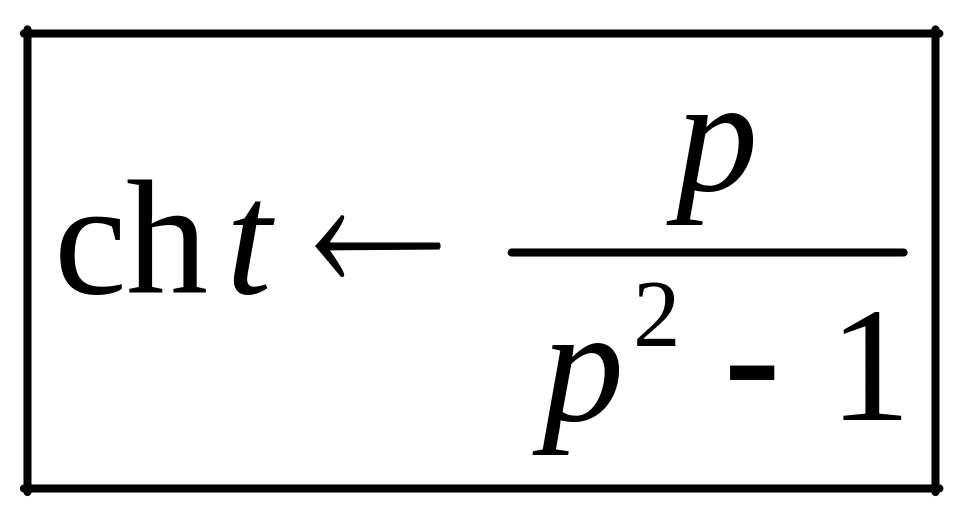Таблица изображений основных элементарных функций

1		7		13
2		8		14
3		9		15
4		10		16
5		11		17
6		12		18

Пример

Найти изображение оригинала , используя таблицу и свойство линейности.

Решение: .

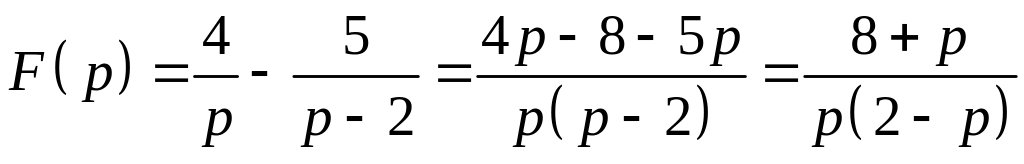Вопрос 3. Теоремы подобия, смещения, запаздывания.

Теорема подобия. Если – оригинал и – его изображение по Лапласу , , тогда для любого постоянного

, .

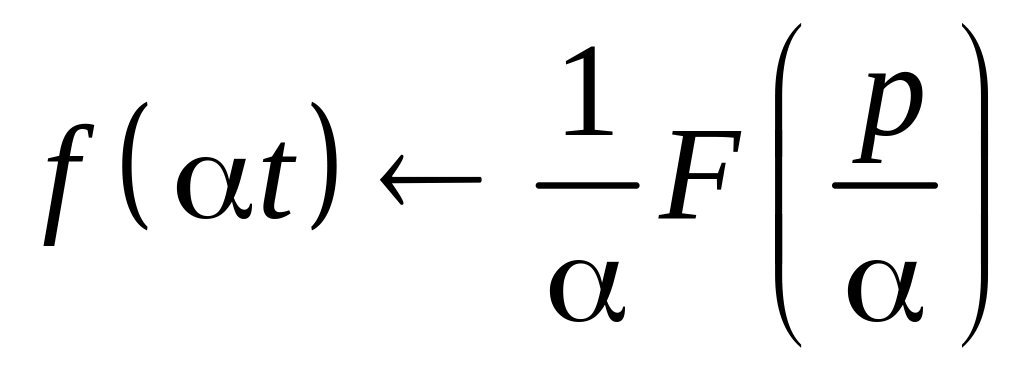Доказательство.

.

Таким образом, умножение аргумента оригинала на положительное число  приводит к делению изображения и его аргумента на это число.

Пример

Пользуясь этой теоремой из формулы можно получить

.

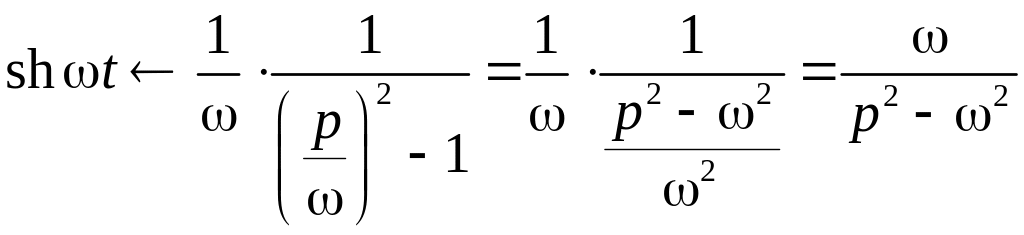Аналогично можно получить .

Пусть задана функция при и при , .

Рассмотрим функцию 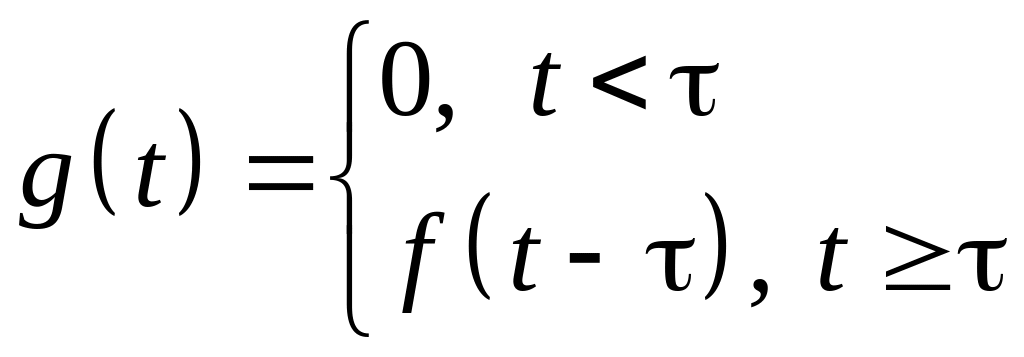, где  – положительное число.

0 t

0  t

График функции можно получить из графика функции путем сдвига последнего на величину  вдоль оси t.

Таким образом, если определяет течение во времени некоторого процесса, то функция определяет тот же процесс, но начавшийся с опозданием .

С помощью единичной функции Хевисайда запаздывающую функцию можно записать так

,

ибо при (в этом случае аргумент отрицателен) и при .

Теорема запаздывания. Если , то для любого положительного 

.

То есть, запаздывание аргумента оригинала на положительную величину  приводит к умножению изображения оригинала без запаздывания на .

Доказательство.

Так как при , то

Положим . При получаем , при имеем . Тогда

.

Пример

Найти изображение оригинала .

Решение

Здесь функция – функция , но «включенная» с запаздыванием . Так как , то по теореме запаздывания получим

.

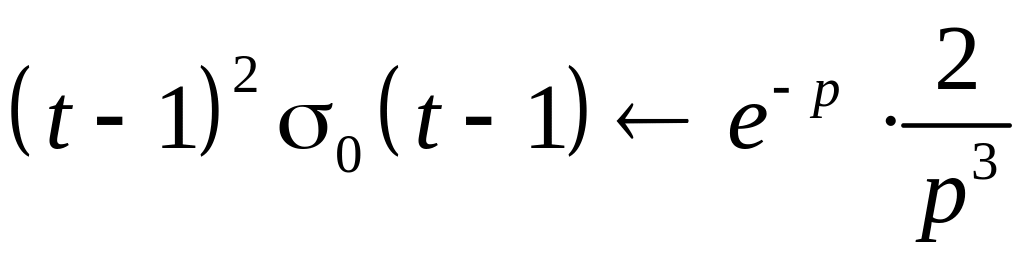Замечание. Если бы мы рассматривали функцию , то эта функция означает оригинал без запаздывания. Изображение этой функции .

На практике часто приходится иметь дело с затухающими функциями, затухание которых происходит по экспоненте (показательному закону). Спрашивается, можно ли найти изображение функции с таким затуханием, если известно изображение функции без затухания? На этот вопрос отвечает теорема.

Теорема смещения Если , то для любого комплексного числа

.

Доказательство.

Эта теорема позволяет по известным изображениям функций находить изображения тех же функций, умноженных на показательную функцию .

Примеры

Используя , получим .

Используя , получим .

Пример

Найти изображение функции, заданной графически.

4 2 1 0 1 2 3 t

Решение. Запишем аналитическое выражение функции:

При функция ; в момент включается функция , в момент она гасится и включается функция ; в момент она гасится и включается функция ; в момент она гасится. Эту последовательность можно записать так:

,

тогда .

Выводы.

1. Преобразованием Лапласа заданной функции действительной переменной t называется преобразование, ставящее в соответствие функции функцию комплексного переменного р, определенную с помощью интеграла (2).

2. Функция (удовлетворяющая условиям 1) – 3)) называется оригиналом (прообразом), а функция – изображением Лапласа функции (или, короче, изображение, образ).

3. Единичная функция Хевисайда «гасит» (обращает в нуль) заданную функцию при .

4. Если две непрерывные функции и имеют одно и то же изображение, то эти функции тождественно равны: .

5. Изображение суммы нескольких функций, умноженных на постоянные, равно сумме изображений этих функций, умноженных на соответствующие постоянные (свойство линейности изображения).

6. Умножение аргумента оригинала на положительное число  приводит к делению изображения и его аргумента на это число (теорема подобия).

7. Запаздывание аргумента оригинала на положительную величину  приводит к умножению изображения оригинала без запаздывания на (теорема запаздывания).

8. Теорема смещения позволяет по известным изображениям функций находить изображения тех же функций, умноженных на показательную функцию .

10