Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Московский государственный индустриальный университет (ГОУ МГИУ) |
Кафедра электротехники, теплотехники, гидравлики и энергетических машин |
ЛАБОРАТОРНАЯ РАБОТА № 3
|
||
по дисциплине «Электротехника и электроника» _________________________________________________________________
|
||
на тему «АНАЛИЗ ЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА В УСТАНОВИВШЕМСЯ РЕЖИМЕ»
|
||
Группа
|
5123 |
|
Студент |
|
Кривошеев К.И. |
Допускается к защите Дата |
___________ |
«___» ___________
|
Преподаватель |
|
Алексеев Д.П. |
Оценка работы Дата |
___________ |
«___» ___________ |
Преподаватель |
|
Алексеев Д.П. |
МОСКВА 2010
1.Цель работы
Цель работы: исследование основных свойств линейных электрических цепей с гармоническими (синусоидальными) источниками ЭДС, применяя на практике метод комплексных амплитуд.
2.Основные положения теории
Для решения основных задач анализа
гармонических колебаний в линейных
электрических цепях преимущественно
используется метод, основанный на замене
операций над синусоидальными функциями,
описывающими колебания, операциями над
комплексными числами, содержащими
полную информацию о параметрах колебаний.
Возможность подобной замены обусловлена
тем, что в режиме гармонических колебаний
все колебания имеют одну и ту же заранее
известную частоту. Тогда функция
,
описывающая гармоническое колебание
известной частоты, характеризуется
лишь двумя вещественными числами:
амплитудой -
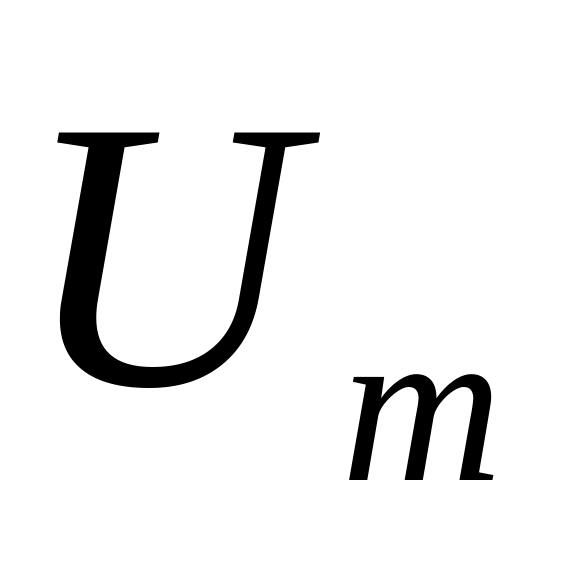
и начальной фазой -
(рис.1.а).
Эти два числа можно объединить в одно
комплексное число
(рис.1.б),
которое может рассматриваться как
символическое изображение синусоидальной
функции.
Комплексное число
,
модуль которого равен амплитуде, а
аргумент – начальной фазе функции,
описывающей гармоническое колебание
,
называться комплексной амплитудой
колебания (напряжения, тока). Для
комплексных амплитуд колебаний формально
верны законы Кирхгофа и Ома, поэтому
при анализе электрических цепей можно
применять все методы, правила и формулы,
используемые при анализе резистивных
электрических цепей. Отличие будет
заключаться лишь в том, что вместо
терминов «напряжение», «ток»,
«сопротивление», «проводимость»
используются термины «комплексная
амплитуда напряжения», «комплексная
амплитуда тока», «комплексное
сопротивление», «комплексная проводимость»
элементов (ветвей) цепи.
Комплексным сопротивлением
двухполюсника
(комплексом полного сопротивле-ния)
называется отношение комплексных
амплитуд напряжения и тока на входе
двухполюсника. Схемное обозначение
двухполюсника приведено на рис. 2.а.
В соответствии с определением
,
где
-
комплексная проводимость (комплекс
полной проводимости) двухполюсника.
Для упрощения обозначений вместо
комплексных амплитуд колебаний
и
принято составлять уравнения для
комплексных действующих значений
.
В простейших случаях, когда двухполюсник представляет собой пассивный элемент электрической цепи, коэффициенты, связывающие между собой комплексные действующие значения напряжений и токов, определяется как:
;
;
;
;
;
и являются комплексными сопротивлениями, соответственно, индуктивности, резистив-ного сопротивления и емкости.
Коэффициенты обратные к приведенным выше:
;
;
;
;
являются комплексными проводимостями соответствующих элементов.
Комплексное сопротивление и комплексная проводимость двухполюсника при произвольном соединении элементов, входящих в его состав, соответственно, равны:
;
,
где
и
-
эквивалентные активные составляющие,
соответственно, комплексного сопротивления
и комплексной проводимости двухполюсника;
и
- эквивалентные реактивные составляющие,
соответственно, комплексного сопротивления
и комплексной проводимости двухполюсника.
Используя показательную форму записи комплексных чисел можно записать:
;
;
;
,
где
и
- модуль, соответственно, комплексного
сопротивления и комплексной проводимости
двухполюсника (в дальнейшем для модулей
сопротивлений и проводимостей будут
использоваться также и сокращенные
обозначения
и
);
Z и Y - аргументы, соответственно, комплексного сопротивления и комплексной проводимости двухполюсника.
Так как
,
а
,
то в этих выражениях:
;
;
;
.
Рассмотрим ряд простейших примеров, иллюстрирующих вычисление и преобразование комплексных сопротивлений и проводимостей двухполюсников. На рис.2.б приведена схема двухполюсника, содержащего индуктивность и резистивное сопротивление, соединенные последовательно. Так как при последовательном соединении двух-полюсников их сопротивления суммируются, то комплексное сопротивление рассматриваемого двухполюсника, при записи в алгебраической форме, будет таким:
,
где активная и реактивная составляющие,
соответственно, равны
,
а
.
Модуль сопротивления двухполюсника
равен модулю
,
т.е.
,
а аргумент Z
= arctg
/R;
поэтому в показательной форме записи
.
Комплексная проводимость
рассматриваемого двухполюсника такова:
.
Чтобы представить
в
алгебраической форме, следует числитель
и знаменатель
умножить на комплексную величину,
сопряженную со знаменателем, тогда
,
где
,
а
.
В показательной форме записи
.
Значит
;
.
Для двухполюсника
из последовательно соединенных
резистивного и емкостного элементов
(рис.2в) аналогично находим
.
Следовательно,
;
;
;
. В последнем выражении
и
,
поэтому
,
а значит
;
.
Наконец
;
и
.
На рис.2г приведена схема двухполюсника, содержащего три соединенные параллель-ные ветви с комплексными проводимостями:
;
;
.
При параллельном соединении двухполюсников их комплексные проводимости суммируются, поэтому:
,
или
.
Следовательно,
;
;
;
.
По закону Ома в комплексной форме:
;
;
;
;
.
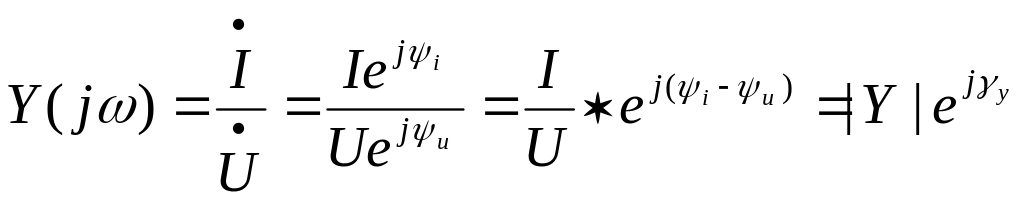Здесь U,
I
- действующие значения напряжения и
тока, которые могут быть определены по
показаниям вольтметра. При этом I
может определяться косвенным
путем через напряжение
,
измеряемое вольтметром на активном
сопротивлении R,
т.е. I=UR
/R.
.
Для пассивных двухполюсников аргументы
комплексных сопротивлений и проводи-мостей
могут изменяться от 0 до
, т.е.
и
.
Угол
положителен при индуктивном характере
цепи (при этом ток отстает по фазе от
напряжения, т.е.
)
и отрицателен при емкостном (при этом
ток опережает по фазе напряжения, т.е.
).
Совокупность векторов, графически изображающих синусоидальные токи, напряжения и ЭДС цепи, называют векторной диаграммой цепи. Построение векторных диаграмм при последовательном соединении элементов цепи следует начинать с построения вектора тока.
Векторная диаграмма цепи, представленной на рис.2б, приведена на рис. 3а. Разделив каждый вектор треугольника напряжений на ток I, получаем треугольник сопротивлений (рис.3б).
Построение векторной диаграммы при параллельном соединении двухполюсников следует начать с вектора напряжения. Векторная диаграмма для цепи, представленной на рис.2г приведена на рис.4.
Комплексная мощность цепи
может быть определена как
Где
- комплексная величина, сопряженная с
комплексным током
;
-
активная мощность цепи
;
-
реактивная мощность цепи
.